Tensorflow基础：神经网络优化算法

Tensorflow基础：神经网络优化算法

本文主要介绍如何通过反向传播算法（backpropagation）和梯度下降算法（gradient decent）调整神经网络中参数的取值。神经网络模型中参数的优化过程直接决定了模型的质量，是使用神经网络时非常重要的一步。
假设用$\theta$表示神经网络中的参数，$J(\theta)$表示在给定的参数取值下，训练数据集上损失函数的大小，那么整个优化过程可以抽象为寻找一个参数$\theta$，使得$J(\theta)$最小。

神经网络的优化过程可以分为两个阶段：

1. 先通过前向传播算法计算得到预测值，并将预测值和真实值做对比得出两者之间的差距。
2. 通过反向传播算法计算损失函数对每一个参数的梯度，再根据梯度和学习率使用梯度下降算法更新每一个参数。

梯度下降算法

梯度下降算法会迭代式更新参数$\theta$，不断沿着梯度的反方向让参数朝着总损失更小的方向更新。

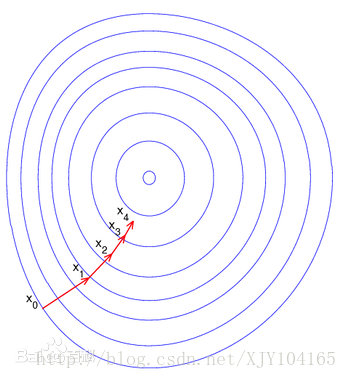
参数的梯度可以通过求偏导的方式计算，对于参数$\theta$，其梯度为$\frac{\partial}{\partial \theta}J(\theta)$。有了梯度，还需要定义一个学习率$\eta$来定义每次参数更新的幅度。参数更新公式为：

$$\theta_{n+1}=\theta_n-\eta \frac{\partial}{\partial \theta}J(\theta_n)$$

随机梯度下降算法（SGD）

除了不一定能达到全局最优外，梯度下降算法的另外一个问题就是计算时间太长。因为要在全部训练数据上最小化损失，所以损失函数$J(\theta)$是在所有训练数据上的损失和。
为了加速训练过程，可以使用随机梯度下降的算法（stochastic gradient descent）。这个算法优化的不是在全部训练数据上的损失函数，而是在每一轮迭代中，随机优化某一条训练数据上的损失函数。
它的问题也非常明显：在某一条数据上损失函数更小并不代表在全部数据上损失函数更小，于是使用SGD甚至可能无法达到局部最优。

为了综合梯度下降算法和随机梯度下降算法的优缺点，实际中一般采用折中的方法—每次计算一小部分训练数据（batch）的损失函数。以下代码给出了在Tensorflow中如何实现神经网络的训练过程：

batch_size = n

x = tf.placeholder(tf.float32, shape=(batch_size, 2), name="x-input")
y_ = tf.placeholder(tf.float32, shape=(batch_size, 1), name="y-input")

loss = ...
train_step = tf.train.AdamOptimizer(0.001).minimize(loss)

with tf.Session() as sess:
    #参数初始化
    #迭代的更新参数
    for i in range(STEPS):
        #准备batch_size个训练数据
        #更好的优化效果
        current_X, current_Y = ...
        sess.run(train_step, feed_dict={x: current_X, y_: current_Y})