傅立叶变换就是从时域和频域来描述问题。每个人的生命之中,时间轴所看到的现象,就是我们的时域,如果时间静止在这一刻,那么在这一刻,现在的你正在走的路、正在看的书和正在爱的人,这些所得到的信息这就是频域中所看到的信息,在时域中,我们看到的是走过的路、读过的书和爱过的人(在这里请注意字眼“正在爱”和“爱过的”,请在此自觉抠字眼)。
如果还不懂,不要紧,请继续往下看,请最后一定要回来体会上一段话。
傅立叶变换就像闹钟(带指针的),我们看闹钟是时针和分针一直在走动,我们了解到自己所处的时间点和指针所循环走动的轨迹就是时域看到的信息。当时间定格在某一刻时,进行纵向(频域)分析,它现在的状态就是齿轮+电池+外壳+走针+等等,这就是从频域获取信息。如果电池电量过低,时钟的走时就会变慢,但是平时我们眼中仅仅从外观(时域)看待问题,并不知道问题出在哪。那么,有意思的事情来了,我们将闹钟“肢解”(频域),就可以很简单的发现,原来是电池坏了!原来原因在这里!
现在我要暗黑的展示出大家经常看到的傅立叶变换都会列出来的四大“神图”!
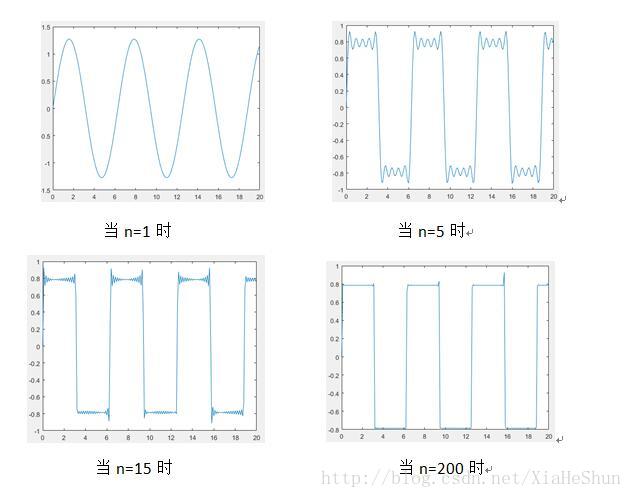
书中所写所画,太粗暴,也没有详细说明,在此只想吐槽以下教材,也不说明一下,并且给的是复指数形式的。我将在这里用MATLAB画出来自定义例子的图像,大家会感觉到原来方波还可以这么玩,可以去逼近。
我在这里通过傅立叶级数中的三角形式来展示,法国数学家傅立叶发现任何一个周期函数只要满足一定条件都可以通过正弦函数和余弦函数构成的无穷级别,即以不同的频率的正弦和余弦函数的加权和表示,在后世称为傅立叶级数(此段话摘抄与MATLAB数字图像信号处理与识别之中,每一个字都形容的极其恰当,不敢在此妄自造作)。
周期为 的函数 的三角形式傅立叶级数展开为:
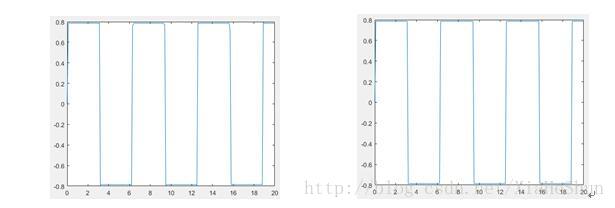
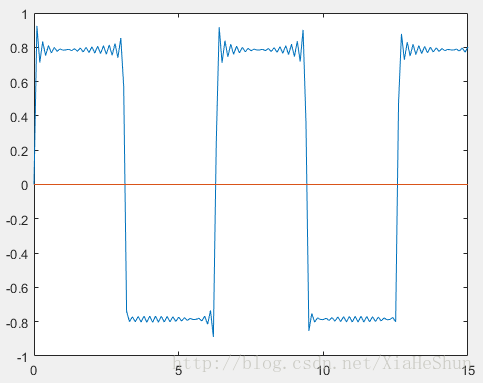
看到n分别取1,5,15,200,400,10000时,你所看到的图像越来越逼近于一个方波,是不是都有点不相信自己的眼睛了,不要怀疑自己,你没有看错,当n取无穷大的时候,他就是方波。
也许看到这里,你半信半疑的相信了傅立叶说的话,任何一个周期函数只要在一定的条件下,都可以使用不同频率的正弦函数或者余弦函数来表示。
Stop!你一定想说:你举的例子与傅立叶变换中的时域和频域有什么关系哦,你分明是在跑题啊!
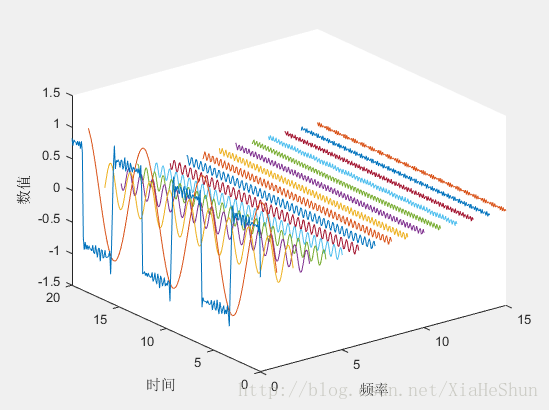
No!在此,我是为了满满的铺垫,就是为了引出下一个图!堪称(自我认为)是傅立叶变换最艺术的表达方式,简直就是傅立叶变换的“名片”。
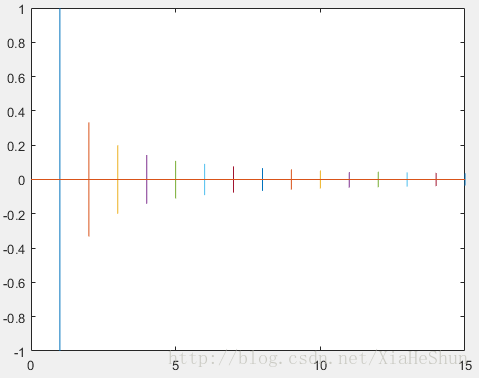
有没有发现,频率为0的时候和那好几个图中n=15时的图像是如此的相似,对没错,那就是它。那后面那些越来越“密集的波浪”是什么呢?请让我解释。
后面的“波浪”是我将n=15时,每一项中的正弦函数按照频率大小排序,依次画出:
现在我们就可以通过超级简单的加减来解释复杂的函数了,在这里也很好的诠释了,无穷个不同频率的正弦函数相加可以表达一个复杂周期函数。我们可以通过傅里叶变换将复杂函数拆分成简单的正弦函数,是不是有一种超级简单的感觉了?!
现在,请你在脑海中回忆我在开头说的话,傅立叶变换对应着我们的人生,在时域中看到的是我们走过的路,读过的书和爱过的人,在频域中看到的是我们正在走的路,正在读得书和正在爱的人。
①当我们从时间轴方向看过去,也就是从时域角度解读问题的,如下图(时域图像):
②当我们从频率轴方向看过去,也就是从频域角度解读问题,如下图(频谱图像):
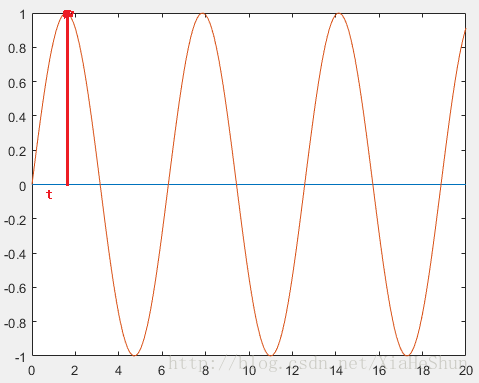
③取最近最高点到某一时间点的时间差t,如下图(此处列出正弦函数图像举例):
此时的相位谱中相位差的大小就为: (此处T为该正弦函数的周期)
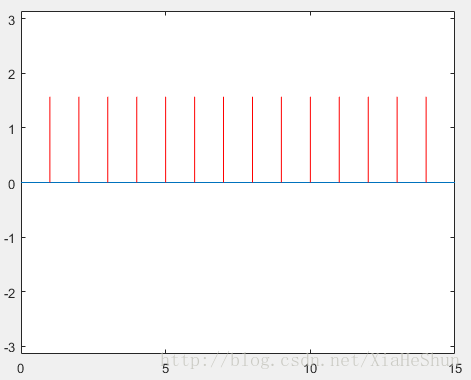
当我们从下往上看的时候,就是从相位差看待问题,如下图(相位谱图像):
上述的①②③分别说明了:时域图像、频率谱图像和相位谱图像。联系上面的实验图,想必也应该有了深刻的了解。










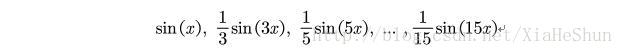
















 4691
4691

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








