Xiaojie雷达之路---TI实战笔记---速度解模糊(基于Doppler相偏补偿)

本篇文章主要讲述的是TI如何基于Doppler相偏补偿进行速度解模糊

背景

1. 为什么要进行速度解模糊呢？
   当一个物体的移动速度超过了雷达可检测的最大速度时，雷达就不能准确的测量物体的速度，因此要增大雷达可检测的最大速度来准确检测目标的速度
2. 利用什么方法进行解模糊呢？
   中国剩余定理、doppler相偏补偿

基础知识

相关速度公式

雷达速度最大检测公式：$V_{max}=\frac{\lambda }{4T_c}$（1），雷达所需要支持$V_{max}$越大，chirp的持续时间$T_c$就要越小

Doppler相偏补偿

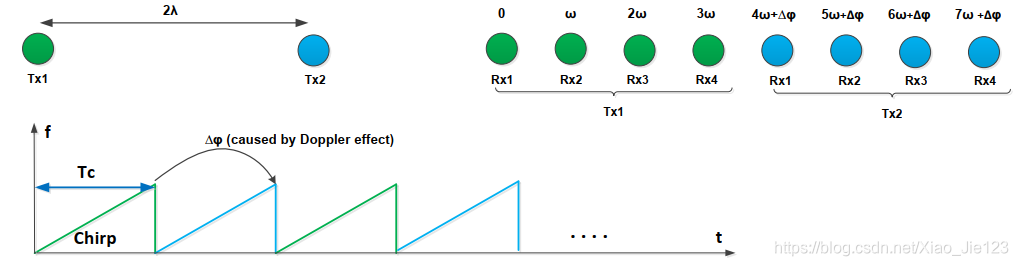
角度分辨率的提高导致最大无模糊速度下降

在上图中，雷达的工作方式是2发4收的TDM MIMO，通过Tx1和Tx2在时间上轮流发射chirp，合并四根接收天线在连续的两个chirp周期内的接收数据，虚拟出1发8收的天线阵列，可以提高角度分辨率。但是，这样就会导致等效的chirp周期($T_c$)相对于1发4收的方式延长了一倍，导致雷达的最大检测速度($V_{max}$)也下降一半

雷达信号处理中对于目标距离和速度的检测是根据2D-FFT结果的幅值进行的，而对于目标角度的检测是根据所有天线(TDM MIMO)上2D FFT对应目标点的相位进行的。在上图中，2发4收 TDM MIMO的工作方式下由于运动目标的多普勒效应，Tx2形成的4根虚拟天线相对于Tx1形成的4根虚拟天线将会产生一个多普勒相偏$\Delta \varphi$。在角度估计前要对多普勒相偏进行矫正，才能保证角度估计的正确性

公式推导：

假设雷达发射的chirp信号为：$s_T(t)=cos(2\pi f_{c}t+{\varphi }_0)$（2）

雷达检测到前方距离为R运动速度为$V_r$的目标的回波信号为：$s_R(t)=cos(2\pi f_c(t-\frac{2(R-V_r{T}_c)}{c})+{\varphi }_0)$（3），$T_c$为发射chirp的周期。

则多普勒相偏为：$\Delta \varphi =2\pi f_c{T}_c=\frac{4\pi V_r{f}_c{T}_c}{c}$（4）

对于发射天线数$N_{Tx}=2$，接收天线数$N_{Rx}=4$的情况，假设在8根虚拟天线($N_{Tx}\ast N_{Rx}=8$)上对应目标的2D-FFT结果序列为$X(m,n)$，其中m表示这个2D-FFT结果对应的发射天线编号($0<m\le N_{Tx}$)，n表示这个2D-FFT结果对应的接收天线编号($0<m\le N_{Rx}$)，那么相偏补偿为下面公式：
$X^{{}^{\prime }}(m,n)=X(m,n)\ast e^{-jm\Delta \varphi }，(0<m\le N_{Tx}，0<m\le N_{Rx})$（5）

由公式(3)可知，只有首先知道目标的实际$V_r$才能知道实际的相偏$\Delta \varphi$，假设雷达的估计的目标速度为$V_{est}$，相偏为$\Delta {\varphi }_{est}$。
$\Delta {\varphi }_{est}=2\pi \Delta f{T}_c=\frac{4\pi V_{est}{f}_c{T}_c}{c}$（6）

目标的实际速度$V_r$和雷达估计出的速度$V_{est}$之间满足公式：
$V_r=V_{est}+k\ast V_{max}，k=\dots ，-1，0，1，\dots$（7）

情况1：$V_r<V_{max}$
当目标的实际速度$V_r$小于雷达最大检测速度$V_{max}$时(k=0)，目标实际速度$V_r$等于雷达估计出的速度$V_{est}$，$V_r=V_{est}$，此时的多普勒相偏$\Delta {\varphi }_{est}$可由$V_{est}$代入公式(4)得到，将$\Delta {\varphi }_{est}$代入公式(5)，可以通过$V_{est}$完全纠正多普勒相偏$\Delta \varphi$，后续的角度FFT可以获得目标角度对应的FFT峰值
情况2：$V_r>V_{max}$
当目标的实际速度$V_r$大于雷达最大检测速度$V_{max}$时($k\ne 0$)，雷达计算的速度是一个模糊值。
$V_r=V_{est}+k\ast V_{max}，k=\dots ，-1，1，\dots$（8）
结合公式(1)，(4)，(6)，(7)，可以得到：$\Delta \varphi =\Delta {\varphi }_{est}+k\ast \pi ，k=\dots ,-1,1,\dots$（9）
从公式(9)可知，目标实际产生的相偏$\Delta \varphi$等于雷达估计出的相偏值$\Delta {\varphi }_{est}$，将修正后的相偏值代入到公式(5)，才能完全纠正多普勒相偏$\Delta \varphi$，后续的角度FFT才可以获得目标角度对应的FFT峰值

TI算法

基于Doppler相偏补偿的速度扩展算法描述

1. 根据公式(6)由雷达估计的目标速度$V_{est}$计算多普勒相偏$\Delta {\varphi }_{est}$
2. 将$\Delta {\varphi }_{est}$代入公式(5)对虚拟天线(m,n)上的目标2D-FFT的结果$X(m,n)$进行多普勒相偏矫正，得到$X^{\prime }(m,n)$
3. 对序列$X^{\prime }(m,n)$进行角度FFT，并计算FFT结果的幅度平方，保存结果到set0，“uncorrected set”
4. 对序列$X^{\prime }(m,n)$按照下面的公式进行符号调整$X^{\prime \prime }(m,n)=conj[X^{\prime }(m,n)]，if(m=1)$
5. 对序列$X^{\prime \prime }(m,n)$进行角度FFT，并计算FFT结果的幅度平方，保存结果到set1，“conrrected set”
6. 在set0和set1中搜索最大值，并记录下最大值所在的set
7. 如果最大值在set1中出现，按照下面的公式进行速度扩展
   $\{\begin{array}{c}{V}_{corr}=V_{est}+2V_{max},if(V_{est}<0)\\ V_{corr}=V_{est}-2V_{max},if(V_{est}>0)\end{array}$
8. 如果最大值在set0中出现，不进行速度扩展
   $V_{corr}=V_{est}$

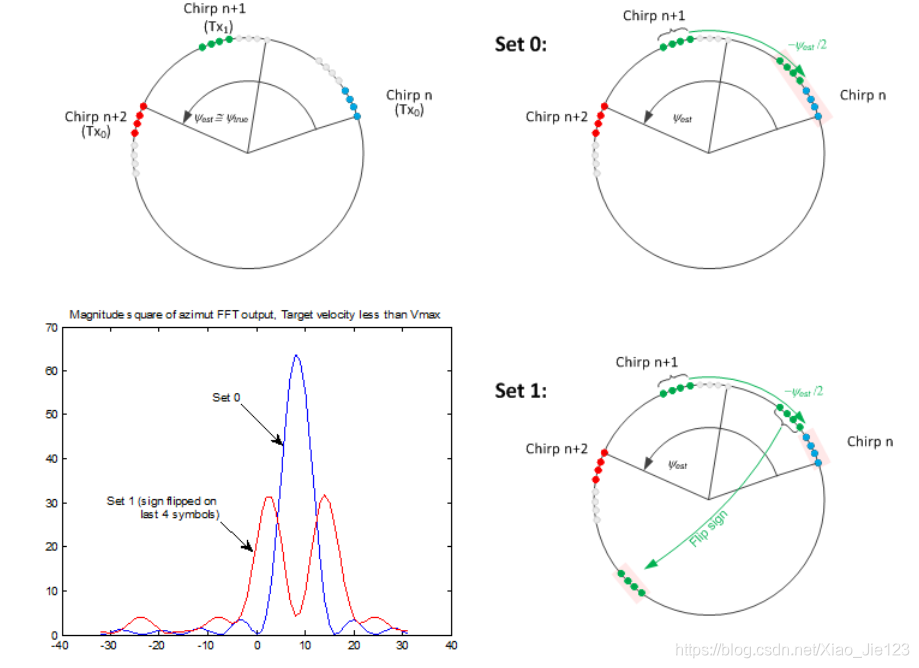
下面两个图分别是在$V_r<V_{max}$和$V_r>V_{max}$情况下，set0和set1中FFT峰值的情况

• $V<V_{max}$
  
• $V>V_{max}$
  
  参考文献：

1. 《AWR1642汽车雷达的速度扩展算法研究》