生成对抗网络——原理解释和数学推导

首先我们有两个关键组件：生成器（G）和判别器（D），一开始我们的G-V1生成了一些手写体的图片，然后丢给D-V1，同时我们也需要把真实图片也送给D-V1，然后D-V1根据自己的“经验”（其实就是当前的网络参数）结合真实图片数据，来判断G-V1生成的图片是不是符合要求。（D是一个二元分类器）
很明显，第一代的G铁定是无法骗过D的，那怎么办？那G-V1就“进化”为G-V2，以此生成更加高质量的图片来骗过D-V1。然后为了识别进化后生成更高质量图的图片的G-V2，D-V1也升级为D-V2……
就这样一直迭代下去，直到生成网络G-Vn生成的假样本进去了判别网络D-Vn以后，判别网络给出的结果是一个接近0.5的值，极限情况就是0.5，也就是说判别不出来了，这就是纳什平衡了，这时候回过头去看生成的图片，发现它们真的很逼真了。
那具体它们是如何互相学习的呢？

首先是判别器（D）的学习：
首先我们随机初始化生成器 G，并输入一组随机向量(Randomly sample a vactor)，以此产生一些图片，并把这些图片标注成 0（假图片）。同时把来自真实分布中的图片标注成 1（真图片）。两者同时丢进判别器 D 中，以此来训练判别器 D 。实现当输入是真图片的时候，判别器给出接近于 1 的分数，而输入假图片的时候，判别器给出接近于 0 的低分。
然后是生成器（G）的学习：
对于生成网络，目的是生成尽可能逼真的样本。所以在训练生成网络的时候，我们需要联合判别网络一起才能达到训练的目的。也就是说，通过将两者串接的方式来产生误差从而得以训练生成网络。步骤是：我们通过随机向量（噪声数据）经由生成网络产生一组假数据，并将这些假数据都标记为 1 。然后将这些假数据输入到判别网路里边，火眼金睛的判别器肯定会发现这些标榜为真实数据（标记为1）的输入都是假数据（给出低分），这样就产生了误差。在训练这个串接的网络的时候，一个很重要的操作就是不要让判别网络的参数发生变化，只是把误差一直传，传到生成网络那块后更新生成网络的参数。这样就完成了生成网络的训练了。
在完成了生成网络的训练之后，我们又可以产生新的假数据去训练判别网络了。我们把这个过程称作为单独交替训练。同时要定义一个迭代次数，交替迭代到一定次数后停止即可。

GAN推导的数学知识

最大似然估计
最大似然估计(Maximum Likelihood Estimation, MLE)，就是利用已知的样本结果信息，反推最具有可能（最大概率）导致这些样本结果出现的模型参数值！样本从某一个客观存在的模型中抽样得来，然后根据样本来计算该模型的数学参数，即：模型已定，参数未知！
考虑一组含有 m 个样本的的数据集 X = { x ( 1 ) , x ( 2 ) , x ( 3 ) , … , x ( m ) } X = \lbrace x^{(1)},x^{(2)},x^{(3)},…,x^{(m)} \rbrace X={x(1),x(2),x(3),…,x(m)} ，独立的由未知参数的现实数据生成分布 $p_{data}(x)$ 生成。
令$p_{model}(x;\theta )$是一个由参数$\theta$(未知)确定在相同空间上的概率分布，也就是说，我们的目的就是找到一个合适的$\theta$使得$p_{data}(x)$尽可能的去接近$p_{data}(x)$
怎么做呢？我们利用真实分布$p_{data}(x)$中生成出来的数据集$X$去估算总体概率为：
$L={\prod }_{i=1}^m{p}_{model}(x^{(i)};\theta )$（1）
然后我们算出使得 $L$最大的这个参数${\theta }_{ML}$,也就是说：对$\theta$ 的最大似然估计被定义为：
${\theta }_{ML}=\underset{\theta }{argmax}{p}_{model}(X;\theta )=\underset{\theta }{argmax}{\prod }_{i=1}^m{p}_{model}(x^{(i)};\theta )$(2)
$p_{model}(X;\theta )\to f(x^{(1)},x^{(2)},x^{(3)},...,x^{(m)}|\theta )$(3)
${\prod }_{i=1}^m{p}_{model}(x^{(i)};\theta )\to f(x^{(1)}|\theta )\cdot f(x^{(2)}|\theta )\cdot f(x^{(3)}|\theta )...f(x^{(m)}|\theta )$(4)
为什么要让$L$最大？我们可以这样想：我们从真实的分布中取得了这些数据
X = { x ( 1 ) , x ( 2 ) , x ( 3 ) , … , x ( m ) } X = \lbrace x^{(1)},x^{(2)},x^{(3)},…,x^{(m)} \rbrace X={x(1),x(2),x(3),…,x(m)}，那为什么我们会偏偏在无穷的真实分布中取得这些数据呢？是因为取得的这些数据的概率更大一点。而此时我们做的就是人工的设计一个由参数 $\theta$控制的分布
$p_{model}(x;\theta )$来去拟合真实分布$p_{data}(x)$ ，换句话说：我们通过一组数据$X$去估算一个参数$\theta$使得这组数据$X$在人工设计的分布中$p_{model}(x;\theta )$被抽样出来的可能性最大，所以让$L$最大就感觉合乎情理了。
多个概率的乘积会因为很多原因不便于计算。例如，计算中很可能会出现数值下溢。为了得到一个便于计算的等价优化问题，我们观察到似然对数不会改变其$argmax$，于是将成绩转换为了便于计算的求和形式：
θ_{ML} = \underset{θ}{arg\ max} \sum_{i=1}^{{m} log p_{model}(x}{(i)};θ)（5）
因为当重新缩放代价函数的时候$argmax$不会改变，我们可以除以$m$得到和训练数据 $X$的经验分布${\hat{p}}_{data}$（当$m\to \infty$,${\hat{p}}_{data}\to p_{data}(x)$）相关期望作为准则：
${\theta }_{ML}=\underset{\theta }{argmax}{E}_{x\sim {\hat{p}}_{data}}log{p}_{model}(x;\theta )$(6)

KL散度
一种解释最大似然估计的观点就是将它看作是最小化训练集上的经验分布${\hat{p}}_{data}$和模型分布 $p_{model}(x;\theta )$之间的差异，两者之间的差异程度就可用KL散度来度量。KL散度(Kullback–Leibler divergence)被定义为：
$D_{KL}({\hat{p}}_{data}||p_{model})=E_{x\sim {\hat{p}}_{data}}[log{\hat{p}}_{data}(x)-log{p}_{model}(x)]$(7)
左边一项仅涉及到数据的原始分布，和模型无关。这意味着当训练模型最小化KL散度的时候，我们只需要最小化：
$-E_{x\sim {\hat{p}}_{data}}[log{p}_{model}(x)]$(8)
额外提一下，它是非对称的，也就是说:
$D_{KL}({\hat{p}}_{data}||p_{model})\ne D_{KL}(p_{model}||{\hat{p}}_{data})$(9)
结合上边对最大似然的解释，开始推导${\theta }_{ML}$：

简述上边的推导：

• 第1行照抄，不赘述；
• 第2行就是直接加上 $log$用来方便后边的运算，连乘变成连加；
• 第3行就是除以$m$得到和训练数据$X$的经验分布${\hat{p}}_{data}$相关的期望；
• 第4行就是把期望展开，后边减去的那一项是为了后边变形为KL散度做准备，这一项不会影响到${\theta }_{ML}$的取值；
• 后边的就是简单的变形而已。

最小化KL散度其实就是在最小化分布之间的交叉熵，任何一个由负对数似然组成的损失都是定义在训练集 $X$的经验分布${\hat{p}}_{data}$和定义在模型上的概率分布 $p_{model}$之间的交叉熵。例如，均方误差就是定义在经验分布和高斯模型之间的交叉熵。

我们可以将最大似然看作是使模型分布$p_{model}$尽可能地与经验分布${\hat{p}}_{data}$相匹配的尝试。理想情况下，我们希望模型分布能够匹配真实地数据生成分布$p_{data}$，但我们无法直接指导这个分布（无穷）。

虽然最优$\theta$在最大化似然和最小化KL散度的时候是相同的，在编程中，我们通常将两者都成为最小化代价函数。因此最大化似然变成了最小化负对数似然(NLL)，或者等价的是最小化交叉熵。

说了这么多数学上的东西，那么要怎么找到一个比较好的$p_{model}(x;\theta )$呢？ 传统的不管是高斯混合模型还是其他的基本模型，都显得过于简单，所以$p_{model}(x;\theta )$在生成对抗网络里是一个神经网络产生的分布，具体的往下看。

假设$z$ 从高斯分布$p_{prior}(z)$中采样而来，然后通过一个神经网络（具体到技术就是：生成模型（G））得到$x$,这个$x$满足另一个分布，然后我们要找到这个分布的参数$\theta$使得它和真实分布越相近越好，在这里$p_{model}(x;\theta )$可以写作：

$p_{model}(x;\theta )={\int }_z{p}_{prior}(z)I_{(G(z)=x)}dx$(17)
其中$I(G(z)=x)$是指示函数。其实就是我们之前学的$log$

这个难点就在于，现实中因为$G(z)$的复杂性，基本上很难找到$x$的经验分布$p_{model}(x;\theta )$ ，而GAN的作用就是在不知道分布的情况下，通过调整参数$\theta$,让生成模型（G）产生的分布尽量接近真实分布。

JS散度
JS散度(Jensen-Shannon divergence)度量了两个概率分布的相似度，基于KL散度的变体，解决了KL散度非对称的问题。一般地，JS散度是对称的，其取值是 0 到 1 之间。定义如下：
$JS(P||Q)=\frac{1}{2}KL(P||\frac{P+Q}{2})+\frac{1}{2}KL(Q||\frac{P+Q}{2})$（18）
在后边推导GAN代价函数的时候会用到，现摆在这里。

KL散度和JS散度度量的时候有一个问题：如果两个分布离得很远，完全没有重叠的时候，那么KL散度值是没有意义的，而JS散度值是一个常数。这在学习算法中是比较致命的，这就意味这这一点的梯度为 0。梯度消失了。

GAN算法推导
首先，重申以下一些重要参数和名词：

1. 生成器(Generator,G)：
   Generator是一个函数，输入是 $z$,输出是$x$;
   给定一个先验分布$p_{prior}(z)$ 和反映生成器G的分布 $P_G(x)$，$P_G(x)$对应的就是上一节的$p_{model}(x;\theta )$;

2. 判别器(Discriminator,D)
   Discriminator也是一个函数，输入是$x$，输出是一个标量；
   主要是评估$P_G(x)$和$P_{data}(x)$之间到底有多不同，也就是求他们之间的交叉熵，$P_{data}(x)$对应的是上一节的$p_{data}(x)$

引入目标公式：$V(G,D)$
$V=E_{x\sim P_{data}}\left[logD(x)\right]+E_{x\sim P_G}\left[log(1-D(x))\right]$（19）
这条公式就是来衡量$P_G(x)$和$P_{data}(x)$之间的不同程度。对于GAN，我们的做法就是：给定 G ，找到一个$D^{\ast }$使得$V(G,D)$最大，即$\underset{D}{\max }V(G,D)$，直觉上很好理解：在生成器固定的时候，就是通过判别器尽可能地将生成图片和真实图片区别开来，也就是要最大化两者之间的交叉熵。

$D^{\ast }=arg\underset{D}{\max }V(G,D)$（20）
然后，要是固定D ，使得$\underset{D}{\max }V(G,D)$最小的这个 G 代表的就是最好的生成器。所以 G 终极目标就是找到 $G^{\ast }$， 找到了$G^{\ast }$我们就找到了分布$P_G(x)$对应参数的${\theta }_G$:
$G^{\ast }=arg\underset{G}{\min }\underset{D}{\max }V(G,D)$(21)
上边的步骤已经给出了常用的组件和一个我们期望的优化目标，现在我们按照步骤来对目标进行推导：

寻找最好的$D^{\ast }$

首先是第一步，给定 G ，找到一个$D^{\ast }$使得$V(G,D)$最大，即求$\underset{D}{\max }V(G,D)$:

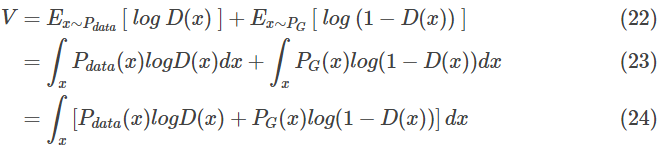
这里假定$D(x)$可以去代表任何函数。然后对每一个固定的 $x$而言，我们只要让 $P_{data}(x)logD(x)+P_G(x)log(1-D(x))$最大，那么积分后的值 $V$也是最大的。
于是，我们设：
$f(D)=P_{data}(x)logD+P_G(x)log(1-D)$（25）

其中$D=D(x)$ ，而$P_{data}(x)$ 是给定的，因为真实分布是客观存在的，而因为 G 也是给定的，所以$P_G(x)$也是固定的。

那么，对$f(D)$求导，然后令$f’(D)=0$，发现：
$D^{\ast }=\frac{P_{data}(x)}{P_{data}(x)+P_G(x)}$（26）
于是我们就找出了在给定的 G 的条件下，最好的 D 要满足的条件。

下图表示了，给定三个不同的 G1，G3，G3 分别求得的令$V(G,D)$最大的那个 $D^{\ast }$，横轴代表了$P_{data}$,蓝色曲线代表了可能的$P_G$，绿色的距离代表了$V(G,D)$：
此时，我们求$\underset{D}{\max }V(G,D)$就非常简单了，直接把前边的$D^{\ast }$代进去。

这部分跟我在ipad上面推导是一样的，当$P_{data}=P_G$时，取到最小值0。也就是说$V(G,D)$存在最小值，且此时$P_{data}=P_G$

寻找最好的$G^{\ast }$
这是第二步，给定$D$,找到一个$G^{\ast }$使得$\underset{D}{\max }V(G,D)$最小，即求$\underset{G}{\min }\underset{D}{\max }V(G,D)$：

根据求得的$D^{\ast }$我们有：

$G^{\ast }=arg\underset{G}{\min }\underset{D}{\max }V(G,D)$
$=arg\underset{G}{\min }\underset{D}{\max }(-2log2+2JSD\left(P_{data}(x)||P_G(x)\right))$

那么根据上式，使得最小化$G$需要满足的条件是：

$P_{data}(x)=P_G(x)$（43）

直观上我们也可以知道，当生成器的分布和真实数据的分布一样的时候，就能让$\underset{D}{\max }V(G,D)$最小。至于如何让生成器的分布不断拟合真实数据的分布，在训练的过程中我们就可以使用梯度下降来计算：

${\theta }_G:={\theta }_G-\eta \frac{\partial \underset{D}{\max }V(G,D)}{\partial {\theta }_G}$(44)

算法总结

1. 给定一个初始的$G_0$；