交叉分类表,是以两个不同时期的地理实体类型为横纵坐标的表格。
①用于参照的时期的类型位于表格的上方,按照横方向排列
②用以比较的时期的类型位于表格的左方,垂直排列
③在横纵坐标上类型的排列顺序一致
④位于对角线上的方格中记录的是两个时期的数据集中没有发生类型变化的单元格数量,非对角线上记录的是从参考时期的类型到比较时期的类型变化的单元格的数量
⑤最后一行和最后一列是分别对行和列的单元格数量的合计
⑥最右下角是研究区域的单元格的总数
根据所得到的交叉表就可以分析从参考时期到比较时期某一种类型的变化情况。例如类型A中没有变化的单元格数量为AA,从A类型变化为B类型的单元格数量为AB••••••,下面通过具体的例子说明交叉表的应用。
为了研究某地区1995~2000年土地利用的变化,取得两个时期土地利用的栅格数据集,并构造交叉表分析两个时期的土地利用变化,交叉表见图2。
(1) 对角线上的数值是没有发生变化的土地利用类型
(2) 对角线外的数值是类型变化的单元格数量。从时期1(1995年)到时期2(2000年)的变化。
(3) 列总数是时期1(1995年)每一种土地利用类型的单元格的总数,行总数是时期2(2000年)的每一种土地利用类型的单元格的总数。
(4) 右下角的总数是研究区域的单元格的总数。
KAPPA指数——KIA:交叉表虽然比较粗糙,却是描述栅格数据随时间的变化以及变化方向的很好的方法。但是交叉表却不能从统计意义上描述变化的程度,需要一种能够测度名义变量变化的统计方法及KAPPA指数法。
KIA主要应用于比较分析两幅地图或图像的差异性是“偶然”因素还是“必然”因素所引起的,还经常用于检查卫星影像分类对于真实地物判断的正确性程度。KIA是能够计算整体一致性和分类一致性的指数。KIA的计算式的一般性表示为:
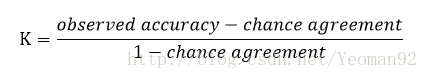
KIA既能够描述总体的一致性,也能够描述分类的一致性。总体KAPPA指数的计算式为:

式中,r为交叉表的行的数量;xii为沿着对角线上的类型组合的数量;xi+为行i的总的观测数;x+i为列的总的观测数量;N为单元格的总数量。
对上式进行适当的变换得到式:
式中,
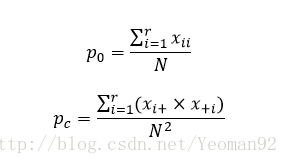
式中的p0和pc都有着明确的含义:p0被称为观测精确性或一致性单元的比例,在土地利用变化分析的例子中表示没有变化的单元的百分比,在遥感图像解释中反映的是解释正确的单元格的比例;pc被称为偶然性一致或期望的偶然一致的单元的比例,在土地利用变化的例子中表示偶然性因素引起的变化的单元格的比例,对于遥感图像解释则表示偶然性因素导致的错误解释的比例。
计算实例:应用前面的交叉表计算总体KAPPA指数。
p0=一致性单元的比例=对角线上元素的和
=(2+4+4+1)/20=0.55
pc=期望的偶然一致的单元的比例
=(2x4)/(20x20)+(9x7)/(20x20)+(8x4)/(20x20)+(1x5)/(20x20)=0.27于是,
KIA=(p0-pc)/(1-pc)=(0.55-0.27)/(1-0.27)=0.3835 对于每一类KAPPA指数的计算方法为:
式中pii为行i,列i上一致性的单元的比例;pi+为行i上期望偶然性一致的单元的比例;p+i为列i上期望偶然性一致的单元的比例。
计算实例:以2000年的土地利用数据作为参考,计算类2中的KIA。
pii=(4/20)=0.2
pi+=(9/20)=0.45
p+i=(7/20)=0.35
KIA=(0.2-0.45x0.35)/(0.45-0.45x0.35)=0.1453 kappa计算结果为-1—1,但通常kappa是落在 0—1 间,可分为五组来表示不同级别的一致性:0.0—0.20极低的一致性、0.21—0.40一般的一致性、0.41—0.60 中等的一致性、0.61—0.80 高度的一致性和0.81—1几乎完全一致。
同样对于评价机器学习模型效果可用kappa指标,把参考时期的数据替换为训练的结果,把比较时期的数据替换为实际的结果。就可以评价训练结果和实际结果的一致性程度了。










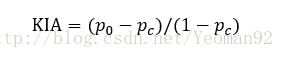















 536
536

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








