[图形学] 《Real-Time Rendering》四元数

 最近四元数用得比较多，虽然对运算和转换已经比较熟悉了，但还是知其然而不知其所以然，所以就再把这本经典之作里的四元数章节好好读了一下，来加深自己的理解

 

       四元数是1843年Sir William Rowan Hamilton作为复数扩展发明的，但是直到1985年，Shoemake才将它们引入计算机图形学领域。四元数是构造变换的非常好的一个工具，在某些方面，四元数要比欧拉角和矩阵更加好，特别是在旋转和方向方面。

       在给定轴&角表示时，将其转换到四元数或者从四元数转换回来都是非常直接的。而将欧拉角转换到任一方向则比较困难。四元数可以用于方向比较平稳的插值，而这是欧拉角无法做到的事情。

       复数具有实部和虚部，每个复数由两个实数来表示，第二个实数要乘以√−1。同样的，四元数有四个部分。前三个值和旋转轴密切相关，而旋转角度影响所有四个部分。每个四元数由四个实数表示，每个实数与不同的部分相关联。由于四元数有四个分量，我们选择将其表示为一个响亮，但是为了区分它们，我们给它带上一个帽子：。我们从四元数的一些数学背景开始，然后用它来构造有趣和有用的变换。

4.3.1 数学背景

        我们从四元数的定义开始:

        定义。一个四元数可以用如下方式定义，所有的都是等价的。

        

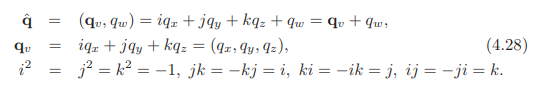
        变量qw称作四元数的实部，。虚部为qv，其中i,j,k称作虚单元。

        对于虚部qv,我们可以使用所有常用的向量运算，如加法、缩放、点积、叉积等。使用四元数的定义，在乘法运算时，下面给出了两个四元数和的计算方式。需要注意的是，虚数单元的乘法是不可交换的。

        

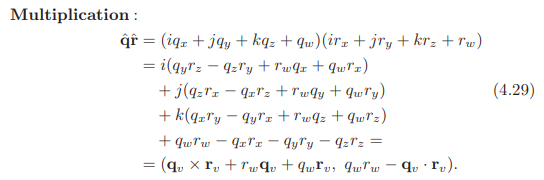
       正如这个方程式中可以看到的，我们使用叉积和点积计算两个四元数的乘法。在四元数定义的基础上，我们还定义了加法、共轭、归一化以及单位四元数。

        

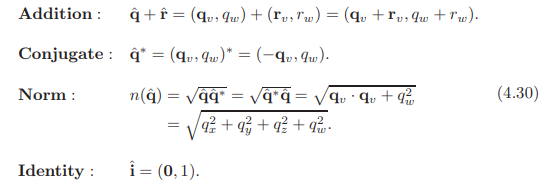
        当被简化（如上所示），虚部被抵消，只剩下实部。归一化有时写作。上述的结果是，我们可以推导出乘法的逆，记作。四元数的逆必须满足等式（这对于乘法的逆运算是通用的）。我们根据归一化的公式推导：

        

       因此，四元数的逆表达为：

        

        四元数逆的公式使用标量乘法，它是从方程式4.29中所示的乘法推导出的这意味着标量乘法是可交换的：

        以下规则也是简单地从定义推导出来的：

        共轭规则：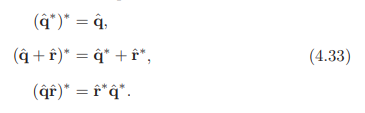

        归一化规则：

        乘法规则：

        线性：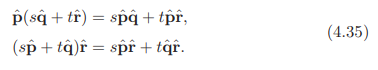

        结合：

       一个单位四元数，即。由此可以看出，q^可以写成：

       

        对于一些三维矢量，可使得，因为

        

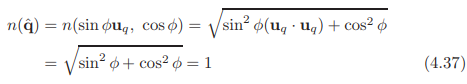
        当且仅当。正如将在下一节中看到的，单位四元数非常适用于以最有效的方式创建旋转以及朝向。但在此之前，我们需要引入单位四元数的一些额外操作。

        对于复数而言，一个二维的单位向量可以写作。四元数的方程可以写作：

        

        单位四元数的对数和幂函数遵循方程4.38:

        对数：

        幂：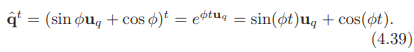

       

4.3.2 四元数变换

        现在我们将研究四元数组的一个子类，即单位长度的子类，称为单位四元数。关于单位四元数的最重要事实是，它们可以表示任何三维旋转，并且非常简洁明了。

        现在我们讲述一下是什么使得四元数在旋转和定向上非常有用。首先，将一个点的四个坐标或者向量p = 作为四元数p的分量，假设我们有一个单位四元数，那么：

        

        将（即点p）绕着轴旋转角度。因为是单位四元数，因此。图4-8显示了这种旋转，它显然可以用来绕任何轴旋转。

        的任何非零实倍数也能表示相同的变换，这意味着和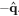表示相同的旋转。也就是说，将轴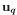和实部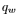反转，将产生一个和原来一样的旋转。这也意味着，从一个矩阵求出的四元数可能是或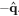

        给定两个单位四元数和，对于一个四元数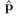（可以看作点p)，首先应用之后再应用的式子如下：

        

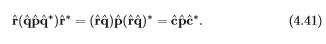
        其中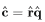，是一个单位四元数，代表了单位四元数和的结合。

  矩阵变换

        由于一些系统有硬件实现的矩阵乘法，而且矩阵乘法比等式4.40更加科学，因此我们需要将四元数转换为矩阵的方法，反之亦然。四元数可以转换为矩阵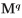，如下式所示：

        

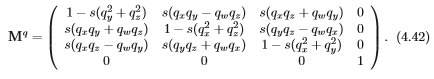
        其中，标量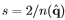，对于单位四元数，这等价于：

        

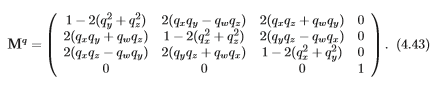
        一旦构造了四元数，就不需要再计算三角函数。因此在实际中转换过程是等同高效的。

        相反的转换，即从正交矩阵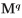到单位四元数会稍微复杂一点。这一过程的关键是由方程4.43中的矩阵的差进行推导：

         

        这些式子的含义是，如果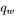是已知的，那么就能求出向量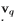的值，进而可求出。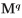的推导计算方式：

        

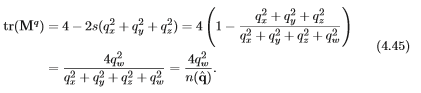
        这个结果产生了单位四元数的下列转换：

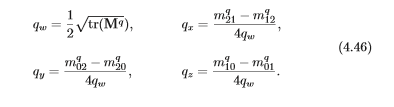
        为了保证例程数字稳定，应该避免小数除法。因此，使得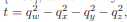，可推出：

        

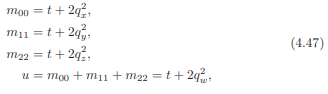
        这意味着m00,m11,m22的最大值决定了qx,qy,qz中的哪个最大。如果qw最大，则使用4.46中的等式推导四元数。否则，我们注意如下：

        

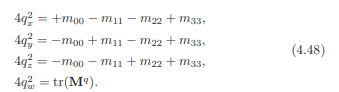
        然后，使用上述方程的适当方程来计算qx,qy,qz的最大值，接着使用方程4.44来计算q的其余分量。幸运的是，已经有了相关源码——请参阅本章末尾的扩展阅读和资源。

  球面线性插值

        球面线性插值是这样的一种操作，给定两个单位四元数和，以及一个参数t 范围(0,1)，计算出插值的四元数。这对于动画物体非常有用。它对于插值相机的方向不是那么有用，因为相机的向上矢量在插值过程中可能变得倾斜，这通常是一种干扰效果。

        这个运算的代数形式由以下复合四元数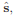表示：

         

       但是，对于软件实现而言，以下形式（slerp代表球面线性插值）更加合适：

       

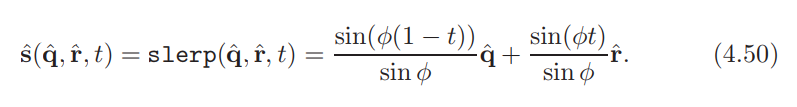
       为了计算该等式中所需的φ，可以使用以下事实：

        

        对于t ∈ [0, 1],slerp函数计算（当且仅当和不相反时）插值四元数，它们一起勾成从(t = 0 )到r（t = 1）的四维单位球上的最短弧。弧位于由，和原点给出的平面与四维单位球面之间的交点形成的圆上。如图4.9所示。计算出的旋转四元数以恒定速度绕固定轴旋转。这样的曲线具有恒定速度并因此加速度为0，被称为测地曲线（geodesic curve）

        

        slerp函数非常适合在两个方向之间进行插值，并且表现良好（固定轴，恒定速度）。当使用几个欧拉角进行插值时，情况则非如此。实际上，直接计算slerp是一项涉及到调用三角函数的昂贵操作。Li提供了更快的增量方法来计算不牺牲任何精度的slerps。

        当两个以上的方向，比如可用时，我们想要从q0到q1到q2进行插值，以此类推直到q(n-1),可以直接使用slerp函数。现在，当我们接近qi的时候，我们会使用qi-1和qi作为slerp的参数。在通过qi之后，我们将使用qi和qi+1作为slerp的参数。这将导致在方向插值中出现突然的抖动，如图4.9所示。这类似于线性插值点时发生的情况，请参阅图13.2的右上角部分。在阅读第13章中的样条曲线，有些读者可能希望重新阅读以下段落。

        插值的更好方法是使用某种样条曲线。我们在qi和qi+1之间引入了四元数ai和ai+1，可以在四元数qi,ai,ai+1和qi+1的集合内定义球面三次插值。惊讶的是，这些额外的四元数计算如下所示：

        其中，qi和ai将用于使用平滑三次样条曲面对四元数进行球面插值，如公式4.52所示：

        

        如上所示，squad函数是使用slerp通过重复的球面插值构建的（请参见13.1.1节对点的重复线性插值信息）。插值将通过初始方向qi, i ∈ [0,...,n − 1]，而不通过ai这些指示初始方向的切线方向来完成。

  从一个向量到另一个的旋转

        通常的操作是通过可能的最短路径从一个方向s转换到另一个方向t。四元数的数学极大地简化了这个过程，并且还显示了四元数与这种表现的紧密关系。首先，归一化s和t，然后计算单位旋转轴，称为u，计算为。接下来，，其中2φ是s和t之间的角度。表示从s到t的旋转四元数则为qˆ = (sin φu, cos φ)。实际上，使用半角关系和三角恒等式可以简化式子

        

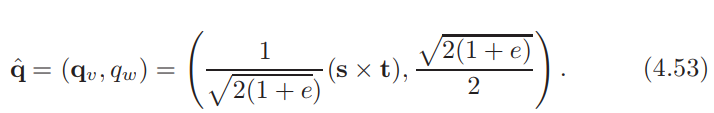
        以这种方式直接生成四元数（相对于对乘积进行归一化）避免了当s和t指向几乎相同方向时数值的不稳定性。当s和t指向相反方向时，两种方法都会出现稳定性问题，因为可能除以0，当检测到这种特殊情况时,任何垂直于s的旋转轴都可以用来直接旋转到t。

        有时我们需要从s到t的旋转矩阵表示。在公式4.43的一些代数和三角函数简化之后，旋转矩阵变为：

        

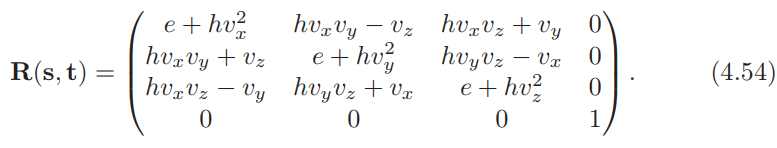
         在这个等式中，我们使用了以下中间计算：

        

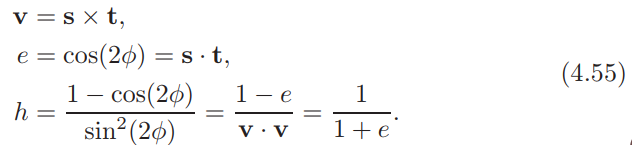
        可以看出，由于简化，所有平方根和三角函数都消失了，因此这是创建矩阵的有效方法。

        注意，当s和t平行或者接近平行时必须小心，因为那样 ||s×t|| ≈ 0，如果φ ≈ 0，那么我们可以返回单位矩阵。但是，如果2φ ≈ π，那么我们可以围绕任何轴旋转π弧度。该轴可以作为s与任何其他与s不平行的向量之间的叉积（参见4.2.4节）。M¨oller 和Hughes使用Householder矩阵以不同的方式处理这种特殊的情况。

        示例：定位和定向相机。假设虚拟相机（或者视点）的默认位置是并且默认视线方向v是沿负z轴的，即。现在，我们的目标是创建一个转换，把相机移动到新的位置p，朝向新的方向。首先定向相机，可以将默认视线方向移动到目标视线方向来完成。R(v, w)将实现这一操作，通过转换为p可以简单地完成定位。这产生了得到的变换。实际上，在第一次旋转之后，很可能需要另一个矢量旋转以将视图的向上方向旋转到某个期望的方向。