【图形学】四元数（二）

4、四元数的推导

  对于轴 $\vec{u}$ 旋转，我们从 $\vec{v}$ 旋转到 $\overrightarrow{v^{\prime }}$，将 $\vec{v}$ 分解为平行于旋转轴 $\text{u}$ 以及正交于 $\text{u}$ 的两个分量，即：
$$v=v_{||}+v_{\perp }$$
  旋转后的分量：
$$v^{\prime }=v_{||}^{\prime }+v_{\perp }^{\prime }$$

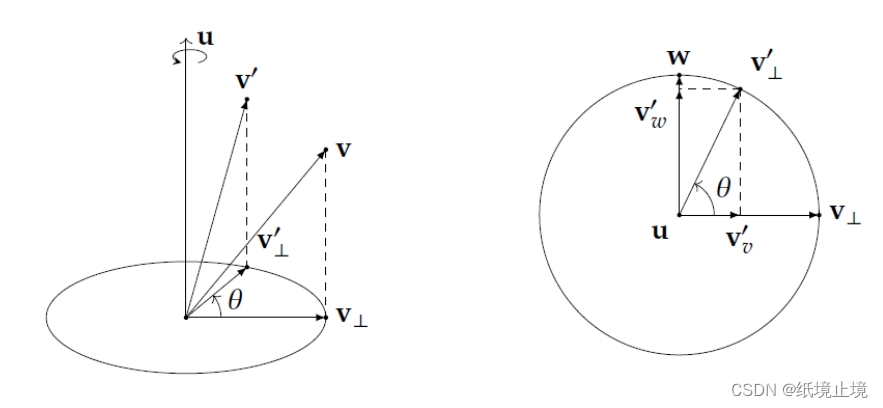
  如图所示，我们可以看到 $v_{||}^{\prime }$ 其实就是 $\vec{v}$ 在 $\vec{u}$ 上的正交投影（Orthogonal Projection）。我们易得：
$$\begin{array}{rlr}{\mathbf{v}}_{\Vert }& ={\mathrm{proj}}_{\mathbf{u}}(\mathbf{v})& \\ & =\frac{\mathbf{u}\cdot \mathbf{v}}{\mathbf{u}\cdot \mathbf{u}}\mathbf{u}& \\ & =\frac{\mathbf{u}\cdot \mathbf{v}}{\Vert \mathbf{u}{\Vert }^2}\mathbf{u}& \left(\Vert \mathbf{u}{\Vert }^2=\mathbf{u}\cdot \mathbf{u}\right)\\ & =(\mathbf{u}\cdot \mathbf{v})\mathbf{u}.& (\Vert \mathbf{u}\Vert =1)\end{array}$$
  又因为 $\mathbf{v}={\mathbf{v}}_{||}+{\mathbf{v}}_{\perp }$，我们可以得到：
$$\begin{gathered} {\mathbf{v}}_{\perp }=\mathbf{v}-{\mathbf{v}}_{||} \\ =\mathbf{v}-(\mathbf{u}\cdot \mathbf{v})\mathbf{u}) \end{gathered}$$
  至此，我们知道了${\mathbf{v}}_{||}$ 和 ${\mathbf{v}}_{\perp }$ 的表达式了。我们对此进行旋转：
  ${\mathbf{v}}_{||}$ 不旋转，而${\mathbf{v}}_{\perp }$ 我们从俯视图看，通过 $\mathbf{u}$ 和 ${\mathbf{v}}_{\perp }$ 能够计算得到一个辅助计算的向量 $\mathbf{w}$。将${{\mathbf{v}}^{\prime }}_{\perp }$ 投影到 $\mathbf{w}$ 和${\mathbf{v}}_{\perp }$上，易得：
$$\begin{array}{rl}{\mathbf{v}}_{\perp }^{\prime }& ={\mathbf{v}}_v^{\prime }+{\mathbf{v}}_w^{\prime }\\ & =\cos (\theta ){\mathbf{v}}_{\perp }+\sin (\theta )\mathbf{w}\\ & =\cos (\theta ){\mathbf{v}}_{\perp }+\sin (\theta )\left(\mathbf{u}\times {\mathbf{v}}_{\perp }\right)\end{array}$$

  又有

  将上面的两个结果组合就可以获得：
$$\begin{array}{rl}{\mathbf{v}}^{\prime }& ={\mathbf{v}}_{\Vert }^{\prime }+{\mathbf{v}}_{\perp }^{\prime }\\ & ={\mathbf{v}}_{\Vert }+\cos (\theta ){\mathbf{v}}_{\perp }+\sin (\theta )\left(\mathbf{u}\times {\mathbf{v}}_{\perp }\right).\\ & =(\mathbf{u}\cdot \mathbf{v})\mathbf{u}+\cos (\theta )(\mathbf{v}-(\mathbf{u}\cdot \mathbf{v})\mathbf{u})+\sin (\theta )(\mathbf{u}\times \mathbf{v})\\ & =\cos (\theta )\mathbf{v}+(1-\cos (\theta ))(\mathbf{u}\cdot \mathbf{v})\mathbf{u}+\sin (\theta )(\mathbf{u}\times \mathbf{v}).\end{array}$$
  这样，我们就得到了一般形式的旋转公式：

5、四元数

  四元数：$q=a+bi+cj+dk,(a,b,c,d\in \mathbb{R})$ ，其中$i^2=j^2=k^2=ijk=-1$ 。我们通常把四元数的 实部 和 虚部 分开，并用一个三维向量来表示虚部，记作：
$$q=[s,\mathbf{v}].(\mathbf{v}=\left[\begin{array}{c}x\\ y\\ z\end{array}\right],s,x,y,z\in \mathbb{R})$$

①模长：

$$||q||=\sqrt{a^2+b^2+c^2+d^2}$$
用标量和向量的方式表示的话，则为：
$$\begin{gathered} ||q||=\sqrt{s^2+||\mathbf{v}|{|}^2} \\ =\sqrt{s^2+v\cdot v} \end{gathered}$$
  显然，四元数的模长很难用几何的方法来进行理解，因为它代表的是一个四维的长度。但是，和高维向量的模长一样，这只是类比复数模长进行衍生定义的结果，你只需要将它理解为一个定义就可以了。

②四元数基本运算

  其实就和普通的向量加法、减法、标量乘法一样了，没有区别。

③BraBmann积

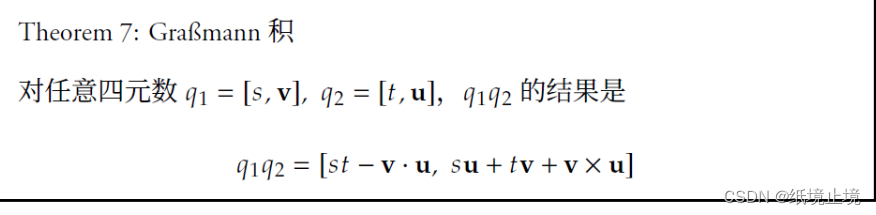
④共轭和逆

  我们规定：$q{q}^{-1}=q^{-1}q=1(q\ne 1)$，其中$q^{-1}$ 为 $q$ 的逆。
  显然，要在无数的四元数中寻找一个满足 $q$的逆 是非常困难的，但是实际上我们可以使用四元数共轭的一些性质来获得 $q^{-1}$。
  我们定义，一个四元数 $q=a+bi+ci+dk$ 的共轭为$q^{\ast }=a-bi-cj-dk$
。如果用标量向量有序对的形式来定义的话，$q=[s,\mathbf{v}]$的共轭为 $g^{\ast }=[s，-\mathbf{v}]$ 。

  共轭四元数的一个非常有用的性质就是：
$$\begin{gathered} q{q}^{\ast }=[s,\mathbf{v}]\cdot [s,-\mathbf{v}] \\ =[s^2-\mathbf{v}\cdot (-\mathbf{v}),s(-\mathbf{v})+s\mathbf{v}+\mathbf{v}\times (-\mathbf{v})] \\ =[s^2+\mathbf{v}\cdot \mathbf{v},0] \\ (\mathbf{v}平行于-\mathbf{v}，所以\mathbf{v}\times (-\mathbf{v})=0) \\ =s^2+x^2+y^2+z^2 \\ =||q|{|}^2 \end{gathered}$$
  根据四元数逆的定义，有：
$$\begin{gathered} q{q}^{-}1=1 \\ {q}^{\ast }q{q}^{-}1=q^{\ast } \\ \left(q^{\ast }q\right)q^{-}1=q^{\ast } \\ ||q|{|}^2\cdot q^{-}1=q^{\ast } \\ {q}^{-}1=\frac{q^{\ast }}{||q|{|}^2} \end{gathered}$$
  最终，如果，$||q||=1$ ，那么 q 就是一个单位四元数（Unit Quaternion），那么：
$$q^{-}1=\frac{q^{\ast }}{1^2}=q^{\ast }$$

⑤纯四元数

  如果一个四元数能写成这样的形式： $ v= [0, \mathbf{v}]$，那么我们称之为一个纯四元数（Pure Quaternion），也就是说，它的实部为 0 。对于两个纯四元数 $v=[0,\mathbf{v}],u=[0,\mathbf{u}]$，则有：
$$\begin{gathered} vu=\left[0-\mathbf{v}\cdot \mathbf{u},0+\mathbf{v}\times \mathbf{u}\right] \\ =\left[-\mathbf{v}\cdot \mathbf{u},\mathbf{v}\times \mathbf{u}\right] \end{gathered}$$

⑥3D旋转公式（四元数型，正交情况）

  我们用 向量 $\mathbf{v}$ 沿着一个用单位向量定义的旋转轴 $\mathbf{u}$ 旋转 $\theta$ 度，成为 ${\mathbf{v}}^{\prime }$ ，我们依然按照平行和垂直的方向拆解这个向量。我们将这些向量定义为纯四元数：
$$\begin{gathered} v=\left[0,\mathbf{v}\right]v^{\prime }=\left[0,{\mathbf{v}}^{\prime }\right] \\ {v}_{\perp }=\left[0,{\mathbf{v}}_{\perp }\right]v_{\perp }^{\prime }=\left[0,{\mathbf{v}}_{\perp }^{\prime }\right] \\ {v}_{||}=\left[0,{\mathbf{v}}_{||}\right]v_{||}^{\prime }=\left[0,{\mathbf{v}}_{||}^{\prime }\right] \\ u=\left[0,\mathbf{u}\right] \end{gathered}$$

  能得到：

  通过这两个分量，我们可以获得一般情况下 $v^{\prime }$ 的结果：
$$\begin{gathered} v^{\prime }=v_{||}^{\prime }+v_{\perp }^{\prime } \\ =v_{||}+q{v}_{\perp } \\ （其中q=cos(\theta ,sin(\theta )\mathbf{u}) \end{gathered}$$

5、3D旋转的矩阵形式

  在实际的应用中，我们可能会需要将旋转与平移和缩放进行复合，所以需要用到四元数的旋转的矩阵形式。比如，我们熟悉的结论：

左乘一个四元数 $q=a+bi+cj+dk$ 等同于下面这个矩阵：
$$\left[\begin{array}{cccc}a& -b& -c& -d\\ b& a& -d& c\\ c& d& a& -b\\ d& -c& b& a\end{array}\right]$$
右乘 $q$ ，等同于这个矩阵：
$$\left[\begin{array}{cccc}a& -b& -c& -d\\ b& a& d& -c\\ c& -d& a& b\\ d& c& -b& a\end{array}\right]$$
  那么我们的结论可以写成：
$$\begin{gathered} qv{q}^{\ast }=L(q)R(q^{-1})v \\ =L(q)R(q^{\ast })v \\ =\left[\begin{array}{cccc}a& -b& -c& -d\\ b& a& -d& c\\ c& d& a& -b\\ d& -c& b& a\end{array}\right]\left[\begin{array}{cccc}a& b& c& d\\ -b& a& -d& c\\ -c& d& a& -b\\ -d& -c& b& a\end{array}\right] \end{gathered}$$
  又因为：$a^2+b^w+c^2+d^2=1$，这个式子能化简为：
$$qv{q}^{\ast }=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1-2c^2-2d^2& 2bs-2ad& 2ac+2bd\\ 0& 2bc-2ad& 1-2b^2-2d^2& 2cd-2ab\\ 0& 2bd-2ac& 2ab+2cd& 1-2b^2-2c^2\end{array}\right]$$
  所以，我们有结论：

（对于目前的状态，四元数学习到这里已经十分够用了_{暂时不拓展了}）