一元线性回归

线性回归也被称为最小二乘法回归(Linear Regression,also called Ordinary LeastSquares(OLS)Regression).它的数学模型是这样的：y=a+b*x+e,其中，a被称位常熟项或截距、b被称为模型的回归系数或斜率、e为误差项。

a和b是模型的参数，当然，，模型的参数只能从样本中估计出来：y’=a’+b’*x，我们的目标是选择合适的参数，让这一线性模型最好地拟合观测值，拟合程度越高，模型越好。我们可以通过用二维平面上的一条直线来表示，被称为回归线，模型的拟合程度越高，也即意味着样本点围绕回归线越紧密。

通常我们通过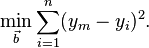来计算样本点与回归线的紧密程度，即：被选择的参数，应该是算出来的回归线与观测值之差的平方和最小。这被称为最小二乘法，其原理为：当预测值和实际值距离的品后方和最小时，就选定模型中的连个参数（a和b）这一模型并不一定反应解是变量和反应变量的真实的关系，但它的计算成本低，相比复杂模型更容易解释。

Stardmodels是python中一个强大的统计分析包，包含了回归分析、时间序列分析、假设检验等等的功能。可以与python的其他任务（如numpy、pandas）有效结合，提高工作效率。

1.读取数据

2.数据可视化

1. 执行最小二乘回归

1. 训练具体模型及其统计量

（使用OLS对象的fit()方法进行模型拟合）

1. 查看模型拟合结果

Result.summary()

 

说明：初学者只关注summary结果中的判定系数，各自变量对应的系数及P值即可。

.R-squared再统计学里脚判定系数，或决定系数，也称拟合优度，值在0到1之间，值越大，表示这个模型拟合的越好，在这里0.991就拟合的很好

.coef:截距

.std err:是标准误差

.t和p：这里对每个系数做了个统计推断，统计推断的原假设是系数为0，表示该系数在模型里不用存在，不用丽姐原理和具体过程，可以直接看p值，P值如果很小，就推腹案原假设，即其实系数不为0，该变量值在模型里都是有意义十的，都应该存在模型里。有些回归问题中，p值比较大，那么对应的变量就可以扔掉。

1. 理论上残差应该服从正态分布，可以检验下

p值很小，拒绝原假设，即残差不服从正态分布

1. 查看残差Durbin-Watson

德宾-沃森检验，简称D-W检验，是目前检验自相关性的最常用方法，但它只使用于检验一阶自相关性。因为自相关系数ρ的值介于-1和1之间，所以0≤DW≤4。并且DW＝O＝＞ρ＝１　　 即存在正自相关性

DW＝４＜＝＞ρ＝－１　即存在负自相关性

DW＝２＜＝＞ρ＝０　　即不存在（一阶）自相关性

因此，当DW值显著接近与0或4时，则存在自相关性，而接近2时，则不存在（一阶）自相关性。这样只要知道DW统计量的概率分布，在给定的显著水平下，更具临界值的位置就可以对原假设H0进行检验。

结果=0.31538，所以残差存在自相关性。

1. 模型预测

9 模型评价（画出预测模型图）

10 模型优化与重新选择

Numpy.column_stack(tup)[source]: Stack 1-D arrays as columns into a 2-D array.

Numpy.power(x1, n): 对数组x1的元素分别求n次方

11.对模型进行预测

12.对优化后的模型作图