数据结构第六章（图）【上】

Zevalin爱灰灰

已于 2024-04-05 15:16:54 修改

阅读量1.5k

点赞数 28

分类专栏：数据结构笔记文章标签：数据结构

于 2024-04-04 15:05:34 首次发布

本文链接：https://blog.csdn.net/Zevalin/article/details/137374979

版权

数据结构笔记专栏收录该内容

12 篇文章 3 订阅

订阅专栏

写在前面：

本系列笔记主要以《数据结构（C语言版）》为参考（本章部分图片来源于王道），结合下方视频教程对数据结构的相关知识点进行梳理。所有代码块使用的都是C语言，如有错误欢迎指出。
视频链接：第01周a--前言_哔哩哔哩_bilibili

一、图的定义和基本术语

1、图的定义

（1）图（Graph）G由两个集合V和E组成，记为G=(V, E)，其中V是顶点的有穷非空集合，E是V中顶点偶对的有穷集合。V(G)和E(G)通常分别表示图G的顶点集合和边集合，E(G)可以为空集，若E(G)为空，则图G只有顶点而没有边。

（2）对于图G，若边集E(G)为有向边的集合，则称该图为有向图；若边集(G)为无向边的集合，则称该图为无向图。

2、图的基本术语

（1）子图：假设有两个图G=(v, E)和G'=(v', E')，如果v'⊆v且E'⊆E，则称G'为G的子图。

（2）无向完全图和有向完全图：

①对于无向图，若具有n(n-1)/2条边（n表示图中顶点数目），则称为无向完全图。

②对于有向图，若具有n(n-1)条弧，则称为有向完全图。

（3）稀疏图和稠密图：有很少条边或弧的图称为稀疏图，反之称为稠密图。

（4）权和网：在实际应用中，每条边可以标上具有某种含义的数值，该数值称为该边上的权值，这些权值可以表示从一个顶点到另一个顶点的距离或耗费，这种带权的图通常称为网。

（5）邻接点：对于无向图G，如果图的边(v, v')∈E，则称顶点v和v'互为邻接点，即v和v'相邻接，边(v, v')依附于顶点v和v'，或者说边(v, v')与顶点v和v'相关联。

（6）度、入度和出度：

①顶点v的度是指和v相关联的边的数目，记为TD(v)；对于有向图，顶点v的度分为入度和出度，入度是以顶点v为头的弧的数目，记为ID(v)，出度是以顶点v为尾的弧的数目，记为OD(v)，顶点v的度为TD(v)= ID(v)+ OD(v)。

②一般地，如果顶点 $v_{i}$ 的度记为TD( $v_{i}$ ），那么一个有n个顶点、e条边的图，满足关系 $e=\frac{1}{2}\sum_{i=1}^{n}TD\left ( v_{i} \right )$ 。

（7）路径、路径长度和带权路径长度：

①在无向图G中，从顶点v到顶点v'的路径是一个顶点序列（ $v=v_{i,0},v_{i,1},\cdots ,v_{i,m}=v'$ ），其中 $(v_{i,j-1},v_{i,j})\epsilon E,1\leq j\leq m$ ；如果G是有向图，则路径也是有向的，顶点序列应满足 $<v_{i,j-1},v_{i,j}>\epsilon E,1\leq j\leq m$ 。

②路径长度是一条路径上经过的边或弧的数目。

③当图是带权图时，一条路径上所有边的权值之和，称为该路径的带权路径长度。

（8）回路或环：第一个顶点和最后一个顶点相同的路径称为回路或环。

（9）简单路径、简单回路或简单环：

①序列中顶点不重复出现的路径称为简单路径。

②除了第一个顶点和最后一个顶点之外，其余顶点不重复出现的回路，称为简单回路或简单环。

（10）连通、连通图和连通分量：

①在无向图G中，如果从顶点v到顶点v'有路径，则称v和v'是连通的。

②如果对于图中任意两个顶点 $v_{i},v_{j}\epsilon V$ ， $v_{i}$ 和 $v_{j}$ 都是连通的，则称G是连通图，连通图最少有n-1条边。

③所谓连通分量，指的是无向图中的极大连通子图，极大连通子图的意思是，该子图是图G的连通子图，且将G的任何不在该子图中的顶点加入后该子图不再连通。

（11）强连通图和强连通分量：

①在有向图G中，如果对于每一对 $v_{i},v_{j}\epsilon V$ ，从 $v_{i}$ 到 $v_{j}$ 和从 $v_{j}$ 到 $v_{i}$ 都存在路径，则称G是强连通图，强连通图最少有n条边。

②有向图中的极大强连通子图称作有向图的强连通分量。

（12）连通图的生成树：一个极小连通子图（极小连通子图是图G的连通子图，在该子图中删除任何一条边，子图不再连通），它含有图中全部顶点，但只有足以构成一棵树的n-1条边，这样的连通子图称为连通图的生成树。

①简单说，生成树是所有顶点均由边连接在一起但不存在回路的图，如果在一棵生成树上添加一条边，必定构成一个环，因为这条边使得它依附的那两个顶点之间有了第二条路径。

②一个图可以有多棵不同的生成树。

（13）有向树和生成森林：

①有一个顶点的入度为0，其余顶点的入度均为1的有向图称为有向树。

②一个有向图的生成森林是由若干棵有向树组成，含有图中全部顶点，但只有足以构成若干棵不相交的有向树的弧。

③对非连通图，由各个连通分量的生成树构成的集合即为生成森林。

（14）简单图和多重图：

①简单图不存在重复边，不存在顶点到自身的边。

②图G中某两个结点之间的边数多于一条，又允许顶点通过同一条边和自己关联，则G为多重图。（下面基本都只讨论简单图）

（15）完全图：任意两个顶点都有一条边相连的图即为完全图，无向完全图共有 $C_{n}^{2}$ 条边，有向完全图共有 $2C_{n}^{2}$ 条边。

二、图的存储结构

1、邻接矩阵

（1）邻接矩阵是表示顶点之间相邻关系的矩阵。设G(V, E)是具有n个顶点的图，则G的邻接矩阵是具有如下性质的n阶方阵：

①无向图的邻接矩阵：

[1]第i个结点的度 = 第i行（或第i列）的非零元素个数。

[2]无向图的邻接矩阵是对称的，在完全图的邻接矩阵中，对角元素为0，其余均为1。

②有向图的邻接矩阵：

[1]第i个结点的出度 = 第i行的非零元素个数，第i个结点的入度 = 第i列的非零元素个数，第i个结点的度 = 第i行、第i列的非零元素个数之和。

[2]有向图的邻接矩阵中，第i行表示以结点 $v_{i}$ 为尾的弧（即出度边），第j列表示以结点 $v_{j}$ 为头的弧（即入度边）。

（2）若G是网，则邻接矩阵可以定义为（边不存在用无穷表示，边存在则用其权值表示）：

（3）用邻接矩阵表示法表示图，除了一个用于存储邻接矩阵的二维数组外，还需要用一个一维数组来存储顶点信息，其形式说明如下：

#define MaxInt 32767  //表示极大值，即无穷
#define MVNum 100     //最大顶点数

typedef char VerTexType;  //假设顶点的数据类型为字符型
typedef int ArcType;      //假设边的权值类型为整型

typedef struct AMGraph
{
	VerTexType vexs[MVNum];      //顶点表
	ArcType arcs[MVNum][MVNum];  //邻接矩阵
	int vexnum, arcnum;          //图的当前点数和边数
}AMGraph;

enum Status
{
	OVERFLOW,
	ERROR,
	OK
};

（4）算法具体实现：

①采用邻接矩阵表示法创建无向图：

Status CreateUDG(AMGraph *G)  //创建无向图G
{
	scanf("%d %d", &G->vexnum, &G->arcnum);  //输入总顶点数和总边数
	for (int i = 0; i < G->vexnum; i++)      //依次输入点的信息
	{
		scanf("%c", &G->vexs[i]);
	}
	for (int i = 0; i < G->vexnum; i++)      //初始化邻接矩阵，此时所有顶点均未连接
	{
		for (int j = 0; j < G->vexnum; j++)
		{
			G->arcs[i][j] = 0;
		}
	}
	for (int k = 0; k < G->arcnum; k++)      //构造邻接矩阵
	{
		VerTexType v1, v2;
		scanf("%c %c", &v1, &v2);     //输入一条边依附的顶点
		int i, j;
		for (i = 0; i < G->vexnum; i++)      //确定v1和v2在G中的位置，即顶点数组的下标
		{
			if (v1 == G->vexs[i])
				break;
		}
		for (j = 0; i < G->vexnum; j++)
		{
			if (v2 == G->vexs[j])
				break;
		}
		G->arcs[i][j] = 1;                  //连接两个顶点
		G->arcs[j][i] = G->arcs[i][j];      //如果建立有向图，删掉该行语句即可
	}
	return OK;
}

②采用邻接矩阵表示法创建无向网：

Status CreateUDN(AMGraph *G)  //创建无向网G
{
	scanf("%d %d", &G->vexnum, &G->arcnum);  //输入总顶点数和总边数
	for (int i = 0; i < G->vexnum; i++)      //依次输入点的信息
	{
		scanf("%c", &G->vexs[i]);
	}
	for (int i = 0; i < G->vexnum; i++)      //初始化邻接矩阵，边的权值均置为无穷大
	{
		for (int j = 0; j < G->vexnum; j++)
		{
			G->arcs[i][j] = MaxInt;
		}
	}
	for (int k = 0; k < G->arcnum; k++)      //构造邻接矩阵
	{
		VerTexType v1, v2;
		ArcType w;
		scanf("%c %c %d", &v1, &v2, &w);     //输入一条边依附的顶点及权值
		int i, j;
		for (i = 0; i < G->vexnum; i++)      //确定v1和v2在G中的位置，即顶点数组的下标
		{
			if (v1 == G->vexs[i])
				break;
		}
		for (j = 0; i < G->vexnum; j++)
		{
			if (v2 == G->vexs[j])
				break;
		}
		G->arcs[i][j] = w;
		G->arcs[j][i] = G->arcs[i][j];      //如果建立有向网，删掉该行语句即可
	}
	return OK;
}

（5）邻接矩阵表示法的优缺点：

①优点：便于判断两个顶点之间是否有边；便于计算各个顶点的度。

②缺点：不便于增加和删除顶点；不便于统计边的数目，需要査找邻接矩阵所有元素才能统计完毕，时间复杂度为O(n2)；空间复杂度高，每次创建图的结构变量时都按最大顶点数申请二维数组，对于稀疏图而言往往用不到那么多空间。

2、邻接表

（1）在邻接表中，对图中每个顶点 $v_{i}$ 建立个单链表，把与 $v_{i}$ 相邻接的顶点放在这个链表中。

（2）邻接表中每个单链表的第一个结点存放有关顶点的信息，把这一结点看成链表的表头，其余结点存放有关边的信息，这样邻接表便由两部分组成：表头结点表和边表。

①表头结点表：由所有表头结点以顺序结构的形式存储，以便可以随机访问任一顶点的边链表；表头结点包括数据域和链域两部分，其中数据域用于存储顶点 $v_{i}$ 的名称或其它有关信息，链域用于指向链表中第一个结点（与顶点 $v_{i}$ 邻接的第一个邻接点）。

②边表：由表示图中顶点间关系的2n个边链表组成；边链表中边结点包括邻接点域、数据域和链域3个部分，其中邻接点域指示与顶点 $v_{i}$ 邻接的点在图中的位置，数据域存储和边相关的信息（如权值等，如果没有要记录的信息则不需要数据域），链域指示与顶点 $v_{i}$ 邻接的下一条边的结点。

③下图的示例中左图是有向图的邻接表，右图是无向图的邻接表。

（3）在无向图的邻接表中，顶点 $v_{i}$ 的度恰为第i个链表中的结点个数；而在有向图中，第i个链表中的结点个数只是顶点 $v_{i}$ 的出度，为求入度，必须遍历整个邻接表。

（4）有时为了便于确定顶点的入度，可以建立一个有向图的逆邻接表，即对每个顶点 $v_{i}$ 建立一个链接所有进入 $v_{i}$ 的边的表。

（5）邻接表的一些性质：

①一个图的邻接矩阵表示是唯一的，但其邻接表表示不唯一，这是因为邻接表表示中，各边表结点的链接次序取决于建立邻接表的算法以及边的输入次序。

②若无向图中有n个顶点、e条边，则其邻接表需n个头结点和2e个表结点，很明显邻接表空间效率高，适合存储稀疏图

③邻接表中每个链表对应于邻接矩阵中的一行，链表中结点个数等于一行中非零元的个数。

（6）要定义一个邻接表，需要先定义其存放顶点的头结点和表示边的边结点，邻接表存储结构说明如下：

#define MaxInt 32767  //表示极大值，即无穷
#define MVNum 100     //最大顶点数

typedef char VerTexType;  //假设顶点的数据类型为字符型
typedef int ArcType;      //假设边的权值类型为整型

typedef struct ArcNode   //边结点
{
	int adjvex;                 //该边所指向的顶点的位置
	struct ArcNode* nextarc;    //指向下一条边的指针
	ArcType info;               //和边相关的信息（比如权值）
}ArcNode;
typedef struct VNode     //顶点信息
{
	VerTexType data;        //和顶点相关的信息（顶点名称）
	ArcNode* firstarc;      //指向第一条依附该顶点的边的指针
}VNode, AdjList[MVNum];      //AdjList表示邻接表类型
typedef struct ALGraph    //邻接表
{
	AdjList vertices;
	int vexnum, arcnum;   //图的当前顶点数和边数
}ALGraph;

enum Status
{
	OVERFLOW,
	ERROR,
	OK
};

（7）算法具体实现：

①采用邻接表表示法创建无向图：

Status CreateUDG(ALGraph *G)  //创建无向图G
{
	scanf("%d %d", &G->vexnum, &G->arcnum);  //输入总顶点数和总边数
	for (int i = 0; i < G->vexnum; i++)      //输入各点，构造表头结点表
	{
		scanf("%c", &G->vertices[i].data);   //输入顶点值（顶点名称）
		G->vertices[i].firstarc = NULL;      //初始化表头结点的指针域为NULL
	}
	for (int k = 0; k < G->arcnum; k++)      //输入各边，构造边表
	{
		VerTexType v1, v2;
		scanf("%c %c", &v1, &v2);            //输入一条边依附的两个顶点
		int i, j;
		for (i = 0; i < G->vexnum; i++)      //确定v1和v2在G中的位置，即顶点在G.vertices中的序号
		{
			if (v1 == G->vertices[i].data)
				break;
		}
		for (j = 0; i < G->vexnum; j++)
		{
			if (v2 == G->vertices[j].data)
				break;
		}
		ArcNode* p1 = (ArcNode*)malloc(sizeof(ArcNode));  //生成一个新的边结点
		p1->adjvex = j;                                   //邻接点序号为j，将新结点*p1插入顶点vi的边表头部
		p1->nextarc = G->vertices[i].firstarc;
		G->vertices[i].firstarc = p1;
		//若生成的是有向图，下面4行代码移除
		ArcNode* p2 = (ArcNode*)malloc(sizeof(ArcNode));  //生成一个新的边结点
		p2->adjvex = i;                                   //邻接点序号为i，将新结点*p2插入顶点vj的边表头部
		p2->nextarc = G->vertices[j].firstarc;
		G->vertices[j].firstarc = p2;
	}
	return OK;
}

②采用邻接表表示法创建无向网：

Status CreateUDG(ALGraph *G)  //创建无向网G
{
	scanf("%d %d", &G->vexnum, &G->arcnum);  //输入总顶点数和总边数
	for (int i = 0; i < G->vexnum; i++)      //输入各点，构造表头结点表
	{
		scanf("%c", &G->vertices[i].data);   //输入顶点值（顶点名称）
		G->vertices[i].firstarc = NULL;      //初始化表头结点的指针域为NULL
	}
	for (int k = 0; k < G->arcnum; k++)      //输入各边，构造边表
	{
		VerTexType v1, v2;
		ArcType w;
		scanf("%c %c %d", &v1, &v2, &w);     //输入一条边依附的两个顶点及其权值
		int i, j;
		for (i = 0; i < G->vexnum; i++)      //确定v1和v2在G中的位置，即顶点在G.vertices中的序号
		{
			if (v1 == G->vertices[i].data)
				break;
		}
		for (j = 0; i < G->vexnum; j++)
		{
			if (v2 == G->vertices[j].data)
				break;
		}
		ArcNode* p1 = (ArcNode*)malloc(sizeof(ArcNode));  //生成一个新的边结点
		p1->adjvex = j;                                   //邻接点序号为j，将新结点*p1插入顶点vi的边表头部
		p1->nextarc = G->vertices[i].firstarc;
		p1->info = w;
		G->vertices[i].firstarc = p1;
		//若生成的是有向网，下面5行代码移除
		ArcNode* p2 = (ArcNode*)malloc(sizeof(ArcNode));  //生成一个新的边结点
		p2->adjvex = i;                                   //邻接点序号为i，将新结点*p2插入顶点vj的边表头部
		p2->nextarc = G->vertices[j].firstarc;
		p2->info = w;
		G->vertices[j].firstarc = p2;
	}
	return OK;
}

（8）邻接表表示法的优缺点：

①优点：便于增加和删除顶点；便于统计边的数目，按顶点表顺序查找所有边表可得到边的数目，时间复杂度为O(n+e)；空间效率高，邻接表或逆邻接表表示的空间复杂度为O(n+e)，适合表示稀疏图。

②缺点：不便于判断顶点之间是否有边；不便于计算有向图各个顶点的度。

3、十字链表

（1）十字链表是有向图的另一种链式存储结构，可以看成将有向图的邻接表和逆邻接表结合起来得到的一种链表。

（2）在十字链表中，对应于有向图中每一条弧有一个结点，对应于每个顶点也有一个结点。

①在弧结点中有5个域，其中尾域和头域分别指示弧尾和弧头这两个顶点在图中的位置，链域hlink指向弧头相同的下一条弧，而链域tlink指向弧尾相同的下一条弧，info域指向该弧的相关信息。

②弧头相同的弧在同一链表上，弧尾相同的弧也在同一链表上，它们的头结点即顶点结点，由3个域组成，其中data存储和顶点相关的信息，如顶点的名称等，firstin和firstout为两个链域，分别指向以该顶点为弧头或弧尾的第一个弧结点。

（3）有向图的十字链表存储表示形式说明如下：

#define MaxInt 32767  //表示极大值，即无穷
#define MVNum 100     //最大顶点数
#define MAX_VERTEX_NUM 20

typedef char VerTexType;  //假设顶点的数据类型为字符型
typedef int ArcType;      //假设边的权值类型为整型

typedef struct ArcBox
{
	int tailvex, headvex;           //该弧的尾和头顶点的位置
	struct ArcBox *hlink, *tlink;   //分别为弧头相同和弧尾相同的弧的链域
	ArcType info;                   //该弧的相关信息（比如权值）
}ArcBox;
typedef struct VexNode
{
	VerTexType data;
	ArcBox *firstin, *firstout;   //分别指向该顶点第一条入弧和出弧
}VexNode;
typedef struct OLGraph
{
	VexNode xList[MAX_VERTEX_NUM];   //表头向量
	int vexnum, arcnum;              //有向图的当前顶点数和弧数
}OLGraph;

4、邻接多重表

（1）邻接多重表是无向图的另一种链式存储结构。

（2）在邻接多重表中：

①每一条边用一个结点表示，它由6个域组成：其中mark为标志域，用以标记该条边是否被搜索过；ivex和jvex为该边依附的两个顶点在图中的位置；ilink指向下一条依附于顶点ivex的边；jlink指向下一条依附于顶点ivex的边；info为指向和边相关的各种信息的指针域。

②每一个顶点也用一个结点表示，它由两个域组成，其中data存储和该顶点相关的信息，firstedge指示第一条依附于该顶点的边。

（3）无向图的邻接多重表存储表示形式说明如下：

#define MaxInt 32767  //表示极大值，即无穷
#define MVNum 100     //最大顶点数
#define MAX_VERTEX_NUM 20

typedef char VerTexType;  //假设顶点的数据类型为字符型
typedef int ArcType;      //假设边的权值类型为整型

typedef enum
{
	unvisited,
	visited
}VisitIf;
typedef struct EBox
{
	VisitIf mark;                    //访问标记
	int ivex, jvex;                  //该边依附的两个顶点的位置
	struct EBox *ilink, *jlink;      //分别指向依附这两个顶点的下一条边
	ArcType info;                    //该边的信息（比如权）
}EBox;
typedef struct VexBox
{
	VerTexType data;
	EBox *firstedge;                 //指向第一条依附该顶点的边
}VexBox;
typedef struct AMLGraph
{
	VexBox adjmulist[MAX_VERTEX_NUM];
	int vexnum, edgenum;               //无向图的当前顶点数和边数
}AMLGraph;

三、图的遍历

1、深度优先搜索

（1）深度优先搜索（Depth First Search，DFS）遍历类似于树的先序遍历，是树的先序遍历的推广。

（2）对于一个连通图，深度优先搜索遍历的过程如下：

①从图中某个顶点v出发，访问v。

②找出刚访问过的顶点的第一个未被访问的邻接点，访问该顶点。以该顶点为新顶点重复此步骤，直至刚访问过的顶点没有未被访问的邻接点为止。

③返回前一个访问过的且仍有未被访问的邻接点的顶点，找出该顶点的下一个未被访问的邻接点，访问该顶点。

④重复步骤2和步骤3，直至图中所有顶点都被访问过，搜索结束。

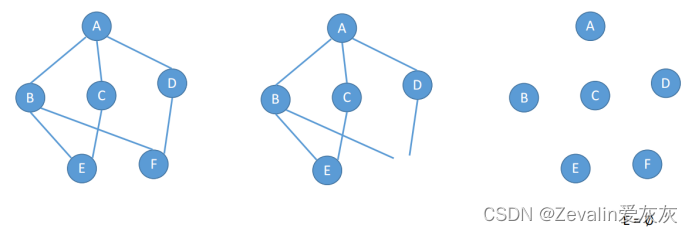
（3）下一图(b)中所示的所有顶点加上标有实箭头的边，构成一棵以v为根的树，称之为深度优先生成树，如下二图(a)所示。

（4）算法具体实现：

①采用邻接矩阵表示连通图的深度优先搜索遍历：

bool visited_AM[MVNum];
void DFS_AM(AMGraph G, int v)  //深度优先搜索遍历连通图
{
	printf("%c", G.vexs[v]);
	visited_AM[v] = true;    //访问第v个顶点，并置访问标志数组相应分量值为true
	for (int w = 0; w < G.vexnum; w++)                //依次检查邻接矩阵v所在行
	{
		if ((G.arcs[v][w] != 0) && (!visited_AM[w]))  //如果w未被访问，则递归调用该函数
			DFS_AM(G, w);
	}
}

②采用邻接表表示连通图的深度优先搜索遍历：

bool visited_AM[MVNum];
void DFS_AMTraverse(AMGraph G)  //对非连通图进行深度优先遍历
{
	for (int v = 0; v < G.vexnum; v++)   //访问标志数组初始化
		visited_AM[v] = false;
	for (int v = 0; v < G.vexnum; v++)
		if (!visited_AM[v])
			DFS_AM(G, v);
}

③采用邻接矩阵表示非连通图的深度优先搜索遍历：

bool visited_AL[MVNum];
void DFS_AL(ALGraph G, int v)  //深度优先搜索遍历连通图
{
	printf("%c", G.vertices[v].data);
	visited_AL[v] = true;    //访问第v个顶点，并置访问标志数组相应分量值为true
	ArcNode* p = G.vertices[v].firstarc;   //p指向v的边链表的第一个边节点
	while (p != NULL)         //边节点非空
	{
		int w = p->adjvex;    //w是v的邻接点
		if (!visited_AL[w])   //如果w未访问，则递归调用该函数
			DFS_AL(G, w);
		p = p->nextarc;       //p指向下一个边节点
	}
}

④采用邻接表表示非连通图的深度优先搜索遍历：

bool visited_AL[MVNum];
void DFS_ALTraverse(ALGraph G)  //对非连通图进行深度优先遍历
{
	for (int v = 0; v < G.vexnum; v++)   //访问标志数组初始化
		visited_AL[v] = false;
	for (int v = 0; v < G.vexnum; v++)
		if (!visited_AL[v])
			DFS_AL(G, v);
}

（5）当用邻接矩阵表示图时，查找每个顶点的邻接点的时间复杂度为O( $n^{2}$ )，其中n为图中顶点数；当以邻接表作为存储结构时，深度优先搜索遍历图的时间复杂度为O(n+e)。由此可得，稠密图适合在邻接矩阵上进行深度遍历，稀疏图适合在邻接表上进行深度遍历。

（6）同一个图的邻接矩阵表示方式唯一，因此深度优先遍历序列唯一；同一个图邻接表表示方式不唯一，因此深度优先遍历序列不唯一。

2、广度优先搜索

（1）广度优先搜索（Breadth First Search，BFS）遍历类似于树的按层次遍历，是树的层次遍历的推广。

（2）广度优先搜索遍历的过程如下：

①从图中某个顶点v出发，访问v。

②依次访问v的各个未曾访问过的邻接点。

③分别从这些邻接点出发依次访问它们的邻接点，并使“先被访问的顶点的邻接点”先于“后被访问的顶点的邻接点”被访问。

④重复步骤3，直至图中所有已被访问的顶点的邻接点都被访问到。

（3）下一图(c)中所示的所有顶点加上标有实箭头的边，构成一棵以v为根的树，称之为广度优先生成树，如下二图(b)所示。

（4）算法具体实现：

①采用邻接矩阵表示连通图的广度优先搜索遍历：

bool visited_AM[MVNum];
void BFS_AM(AMGraph G, int v)  //广度优先搜索遍历连通图
{
	printf("%c", G.vexs[v]);
	visited_AM[v] = true;      //访问第v个顶点，并置访问标志数组相应分量值为true
	SqQueue Q;
	InitQueue(&Q);
	EnQueue(&Q, v);
	while (Q.front != Q.rear)
	{
		int u;
		DeQueue(&Q, &u);
		int w;
		for (w = 0; w < G.vexnum; w++)                  //依次检查邻接矩阵u所在行
		{
			if ((G.arcs[u][w] != 0) && (!visited_AM[w]))  //如果w未被访问
				break;
		}
		while (w < G.vexnum)
		{
			if (!visited_AM[w])
			{
				printf("%c", G.vexs[w]);
				visited_AM[w] = true;
				EnQueue(&Q, w);
			}
			for (w = w + 1; w < G.vexnum; w++)           //依次检查邻接矩阵u所在行
			{
				if ((G.arcs[u][w] != 0) && (!visited_AM[w]))  //如果w未被访问
					break;
			}
		}
	}
}

②采用邻接表表示连通图的广度优先搜索遍历：

bool visited_AL[MVNum];
void BFS_AL(ALGraph G, int v)  //广度优先搜索遍历连通图
{
	printf("%c", G.vertices[v]);
	visited_AL[v] = true;      //访问第v个顶点，并置访问标志数组相应分量值为true
	SqQueue Q;
	InitQueue(&Q);
	EnQueue(&Q, v);
	while (Q.front != Q.rear)
	{
		int u;
		DeQueue(&Q, &u);
		int w;
		ArcNode* p = G.vertices[u].firstarc;   //p指向u的边链表的第一个边节点
		if (p != NULL)
			w = p->adjvex;
		while (w < G.vexnum)
		{
			if (!visited_AL[w])
			{
				printf("%c", G.vertices[w]);
				visited_AL[w] = true;
				EnQueue(&Q, w);
			}
			if (p != NULL)
			{
				w = p->adjvex;
				p = p->nextarc;
			}
			else
				break;
		}
	}
}

③采用邻接矩阵表示非连通图的广度优先搜索遍历：

bool visited_AM[MVNum];
void BFS_AMTraverse(AMGraph G)  //对非连通图进行广度优先遍历
{
	for (int v = 0; v < G.vexnum; v++)   //访问标志数组初始化
		visited_AM[v] = false;
	for (int v = 0; v < G.vexnum; v++)
		if (!visited_AM[v])
			BFS_AM(G, v);
}

④采用邻接表表示非连通图的广度优先搜索遍历：

bool visited_AL[MVNum];
void BFS_ALTraverse(ALGraph G)  //对非连通图进行广度优先遍历
{
	for (int v = 0; v < G.vexnum; v++)   //访问标志数组初始化
		visited_AL[v] = false;
	for (int v = 0; v < G.vexnum; v++)
		if (!visited_AL[v])
			BFS_AL(G, v);
}

（5）当用邻接矩阵存储时，该算法的时间复杂度为O( $n^{2}$ )；用邻接表存储时，该算法的时间复杂度为O(n+e)。

（6）同一个图的邻接矩阵表示方式唯一，因此广度优先遍历序列唯一；同一个图邻接表表示方式不唯一，因此广度优先遍历序列不唯一。

Zevalin爱灰灰

关注

28
点赞
踩
19

收藏

觉得还不错? 一键收藏
打赏
0
评论
数据结构第六章（图）【上】

（1）图（Graph）G由两个集合V和E组成，记为G=(V, E)，其中V是顶点的有穷非空集合，E是V中顶点偶对的有穷集合。V(G)和E(G)通常分别表示图G的顶点集合和边集合，E(G)可以为空集，若E(G)为空，则图G只有顶点而没有边。（2）对于图G，若边集E(G)为有向边的集合，则称该图为有向图；若边集(G)为无向边的集合，则称该图为无向图。
复制链接

扫一扫