个人专栏—塑性力学
1.1 塑性力学基本概念 塑性力学基本概念
1.2 弹塑性材料的三杆桁架分析 弹塑性材料的三杆桁架分析
1.3 加载路径对桁架的影响 加载路径对桁架的影响
2.1 塑性力学——应力分析基本概念 应力分析基本概念
2.2 塑性力学——主应力、主方向、不变量 主应力、主方向、不变量
目录
理想弹塑性加载模型 \color{green}理想弹塑性加载模型 理想弹塑性加载模型
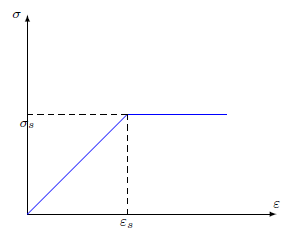
σ
=
{
E
ε
(
ε
≤
ε
s
)
σ
s
(
ε
≥
ε
s
)
\sigma=\begin{cases} E\varepsilon & (\varepsilon\leq \varepsilon_s) \\ \sigma_s & (\varepsilon\geq \varepsilon_s) \end{cases}
σ={Eεσs(ε≤εs)(ε≥εs)
应用示例: \color{green}应用示例: 应用示例:
如图所示,设各杆的初始横截面积均为 $A_0 $,相邻杆间夹角为 $45^{\circ} $,第2根杆的初始长度为 $l_0 $,则第1根和第3根杆的长度均为 $\sqrt{2}l_0 $,用 $F_{N1},F_{N2},F_{N3} $表示1,2和3杆的内力。
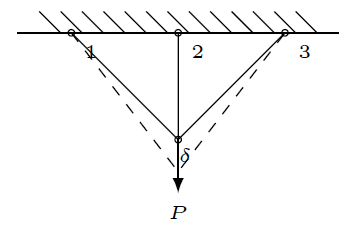
解:
平衡方程
{
F
N
1
=
F
N
2
(
F
N
1
+
F
N
2
)
/
2
+
F
N
2
=
P
→
2
σ
1
+
σ
2
=
P
/
A
0
σ
1
=
F
N
1
/
A
0
σ
2
=
F
N
2
/
A
0
由变形协调关系求得节点的竖向位移
δ
=
ε
2
l
0
=
ε
1
l
1
2
=
2
ε
1
l
0
1杆和2杆应变满足
ε
2
=
2
ε
1
\begin{gather*} \text{平衡方程} \begin{cases} F_{N1}=F_{N2}\\ (F_{N1}+F_{N2})/\sqrt{2}+F_{N2}=P \end{cases}\\ \rightarrow \sqrt{2}\sigma_1+\sigma_2=P/A_0\\ \sigma_1=F_{N1}/A_0\quad \sigma_2=F_{N2}/A_0\\ \text{由变形协调关系求得节点的竖向位移} \\ \delta=\varepsilon_2l_0=\varepsilon_1l_1\sqrt{2}=2\varepsilon_1l_0\\ \text{1杆和2杆应变满足}\quad \varepsilon_2=2\varepsilon_1 \end{gather*}
平衡方程{FN1=FN2(FN1+FN2)/2+FN2=P→2σ1+σ2=P/A0σ1=FN1/A0σ2=FN2/A0由变形协调关系求得节点的竖向位移δ=ε2l0=ε1l12=2ε1l01杆和2杆应变满足ε2=2ε1
弹性阶段 \color{green}弹性阶段 弹性阶段
σ 1 = E ε 1 , σ 2 = E ε 2 → σ 2 = 2 σ 1 { σ 1 = σ 3 = 1 2 + 2 ⋅ P A 0 σ 2 = 2 2 + 2 ⋅ P A 0 当 P 增加时,第2杆首先屈服, σ 2 = σ 2 对应的外载 P e = σ s A 0 ( 1 + 1 2 ) δ e = ε 2 l 0 = σ 2 E l 0 = σ s l 0 / E \begin{gather*} \sigma_1=E\varepsilon_1, \sigma_2=E\varepsilon_2\rightarrow \sigma_2=2\sigma_1\\ \begin{cases} \sigma_1=\sigma_3=\frac{1}{2+\sqrt{2}}\cdot\frac{P}{A_0}\\ \sigma_2=\frac{2}{2+\sqrt{2}}\cdot\frac{P}{A_0} \end{cases}\\ \text{ 当$P $增加时,第2杆首先屈服, $\sigma_2=\sigma_2 $对应的外载}\\ P_e=\sigma_sA_0(1+\frac{1}{\sqrt{2}})\\ \delta_e=\varepsilon_2l_0=\frac{\sigma_2}{E}l_0=\sigma_sl_0/E \end{gather*} σ1=Eε1,σ2=Eε2→σ2=2σ1{σ1=σ3=2+21⋅A0Pσ2=2+22⋅A0P 当P增加时,第2杆首先屈服, σ2=σ2对应的外载Pe=σsA0(1+21)δe=ε2l0=Eσ2l0=σsl0/E
弹塑性阶段 \color{green}弹塑性阶段 弹塑性阶段
当 $P\ge P_e $时,第2杆产生塑性变形,但第1杆和第3杆处于弹性范围,由于材料是理想弹塑性的,进入塑性状态的第2杆应力不再增加
σ
2
=
σ
s
由平衡方程得:
σ
1
=
(
P
A
0
−
σ
s
)
/
2
\begin{gather*} \sigma_2=\sigma_s\\ \text{由平衡方程得:}\quad \sigma_1=(\frac{P}{A_0}-\sigma_s)/\sqrt{2} \end{gather*}
σ2=σs由平衡方程得:σ1=(A0P−σs)/2
继续增加载荷 $P $,使1杆和3杆达到屈服,令 $\sigma_1=\sigma_s $得到外载
塑性极限载荷 P s = σ s A 0 ( 1 + 2 ) δ s = ε 2 l 0 = 2 ε 1 l 0 = 2 σ 1 l 0 / E = 2 σ s l 0 / E = 2 δ e \begin{gather*} \text{塑性极限载荷} \quad P_s=\sigma_sA_0(1+\sqrt{2})\\ \delta_s=\varepsilon_2l_0=2\varepsilon_1l_0=2\sigma_1l_0/E=2\sigma_sl_0/E=2\delta_e \end{gather*} 塑性极限载荷Ps=σsA0(1+2)δs=ε2l0=2ε1l0=2σ1l0/E=2σsl0/E=2δe
卸载 \color{green}卸载 卸载
当 $(P_e\le P\le P_s) $时卸载,卸载服从弹性规律,荷载变化 $\Delta P $时卸载
{ Δ σ 2 = 2 2 + 2 Δ P A 0 = Δ P P e σ s , Δ 1 = Δ 3 = 1 2 + 2 ⋅ Δ P A 0 = Δ P 2 P e σ s Δ ε 2 = Δ σ 2 E , Δ ε 1 = Δ ε 2 = Δ σ 1 E \begin{gather*} \begin{cases} \Delta \sigma_2=\frac{2}{2+\sqrt{2}}\frac{\Delta P}{A_0}=\frac{\Delta P}{P_e}\sigma_s, & \Delta_1=\Delta_3=\frac{1}{2+\sqrt{2}}\cdot\frac{\Delta P}{A_0}=\frac{\Delta P}{2P_e}\sigma_s\\ \Delta\varepsilon_2=\frac{\Delta \sigma_2}{E}, & \Delta \varepsilon_1= \Delta \varepsilon_2=\frac{\Delta\sigma_1}{E} \end{cases} \end{gather*} {Δσ2=2+22A0ΔP=PeΔPσs,Δε2=EΔσ2,Δ1=Δ3=2+21⋅A0ΔP=2PeΔPσsΔε1=Δε2=EΔσ1
若将 $P $全部卸载,即 $\Delta P=P $,则残余应力为
σ
~
2
=
σ
2
−
Δ
σ
2
=
(
1
−
P
P
e
)
σ
s
≤
0
σ
~
1
=
σ
1
−
Δ
σ
1
=
(
P
P
e
−
1
)
σ
s
/
2
≥
0
\begin{gather*} \tilde{\sigma}_2=\sigma_2-\Delta \sigma_2=(1-\frac{P}{P_e})\sigma_s\le 0\\ \tilde{\sigma}_1=\sigma_1-\Delta \sigma_1=(\frac{P}{P_e}-1)\sigma_s/\sqrt{2}\ge 0 \end{gather*}
σ~2=σ2−Δσ2=(1−PeP)σs≤0σ~1=σ1−Δσ1=(PeP−1)σs/2≥0
残余位移和残余应变 \color{green}残余位移和残余应变 残余位移和残余应变
δ ~ = 2 ε ~ 1 l 0 = 2 σ ~ 1 l 0 E = 2 ( P P e − 1 ) δ e ≥ 0 { ε 1 ~ = δ ~ / 2 l 0 = 1 2 σ s E ( P P e − 1 ) = σ 1 ~ / E ε 2 ~ = 2 ε 1 ~ ≥ 0 \begin{gather*} \tilde{\delta}=2\tilde{\varepsilon}_1l_0=2\frac{\tilde{\sigma}_1l_0}{E}=\sqrt{2}(\frac{P}{P_e}-1)\delta_e\ge 0\\ \begin{cases} \tilde{\varepsilon_1}=\tilde{\delta}/2l_0=\frac{1}{\sqrt{2}}\frac{\sigma_s}{E}(\frac{P}{P_e}-1)=\tilde{\sigma_1}/E\\ \tilde{\varepsilon_2}=2\tilde{\varepsilon_1}\ge 0 \end{cases} \end{gather*} δ~=2ε~1l0=2Eσ~1l0=2(PeP−1)δe≥0{ε1~=δ~/2l0=21Eσs(PeP−1)=σ1~/Eε2~=2ε1~≥0
线性强化弹塑性加载模型 \color{green}线性强化弹塑性加载模型 线性强化弹塑性加载模型
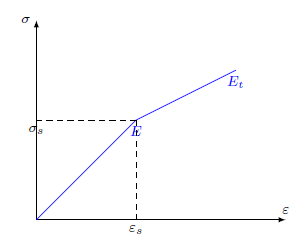
σ = E ε ε ≤ ε s σ = E ε s + E t ( ε − ε s ) ε ≥ ε s = σ s + E t ( ε − ε s ) = σ s + E t E E ( ε − ε s ) = σ s ( 1 − E t E ) + E t ε \begin{align*} \sigma&=E\varepsilon \quad \varepsilon\leq\varepsilon_s\\ \sigma&=E\varepsilon_s+E_t(\varepsilon-\varepsilon_s) \quad \varepsilon\ge\varepsilon_s\\ &=\sigma_s+E_t(\varepsilon-\varepsilon_s)=\sigma_s+\frac{E_t}{E}E(\varepsilon-\varepsilon_s)\\ &=\sigma_s(1-\frac{E_t}{E})+E_t\varepsilon \end{align*} σσ=Eεε≤εs=Eεs+Et(ε−εs)ε≥εs=σs+Et(ε−εs)=σs+EEtE(ε−εs)=σs(1−EEt)+Etε
应用示例: \color{green}应用示例: 应用示例:
各杆的初始横截面积均为 $A_0 $,相邻杆间夹角为 $45^{\circ} $,第2根杆的初始长度为 $l_0 $,则第1根和第3根杆的长度均为 $\sqrt{2}l_0 $,用 $F_{N1},F_{N2},F_{N3} $表示1,2和3杆的内力。
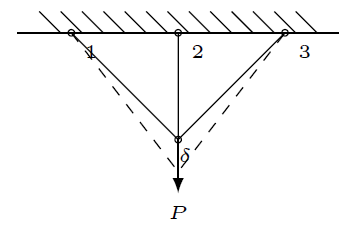
解:设材料是线性强化,应力应变关系为
σ
=
{
E
ε
σ
≤
σ
s
σ
s
+
E
1
(
ε
−
σ
s
E
)
σ
≥
σ
s
\sigma=\begin{cases} E\varepsilon & \sigma\leq \sigma_s\\ \sigma_s+E_1(\varepsilon-\frac{\sigma_s}{E}) & \sigma\ge \sigma_s \end{cases}
σ={Eεσs+E1(ε−Eσs)σ≤σsσ≥σs
当 $P\leq P_e $时,桁架处于弹性阶段,与理想弹塑性材料的三杆桁架弹性阶段分析相同。
当 $P\ge P_e $,第2杆进入塑性强化状态
σ 2 = σ s + E 1 ( ε 2 − σ s E ) { σ 1 = P A 0 − σ s ( 1 − E 1 E ) 2 ( E 1 E + 2 2 ) σ 2 = E 1 E ⋅ P A 0 + σ s ( 1 − E 1 E ) / 2 E 1 E + 2 2 σ 1 = σ 时,1杆进入塑性状态 P 1 = σ s A 0 ( 2 + 1 + E 1 E ) \begin{gather*} \sigma_2=\sigma_s+E_1(\varepsilon_2-\frac{\sigma_s}{E})\\ \begin{cases} \sigma_1=\frac{\frac{P}{A_0}-\sigma_s(1-\frac{E_1}{E})}{2(\frac{E_1}{E}+\frac{\sqrt{2}}{2})}\\ \sigma_2=\frac{\frac{E_1}{E}\cdot\frac{P}{A_0}+\sigma_s(1-\frac{E_1}{E})/\sqrt{2}}{\frac{E_1}{E}+\frac{\sqrt{2}}{2}} \end{cases}\\ \text{$\sigma_1=\sigma$时,1杆进入塑性状态}\\ \quad P_1=\sigma_sA_0(\sqrt{2}+1+\frac{E_1}{E}) \end{gather*} σ2=σs+E1(ε2−Eσs)⎩ ⎨ ⎧σ1=2(EE1+22)A0P−σs(1−EE1)σ2=EE1+22EE1⋅A0P+σs(1−EE1)/2σ1=σ时,1杆进入塑性状态P1=σsA0(2+1+EE1)
如果你喜欢以上内容,或者对塑性力学感兴趣,欢迎一键三连,博主将持续更新,如果有任何问题,可以咨询博主,非常乐意为大家解答。








 本文详细介绍了塑性力学的基本概念,探讨了理想弹塑性加载模型和线性强化弹塑性模型在三杆桁架中的应用,包括应力分析、平衡方程的求解以及不同阶段的材料行为,如弹性阶段、塑性阶段和卸载过程中的应力与位移计算。
本文详细介绍了塑性力学的基本概念,探讨了理想弹塑性加载模型和线性强化弹塑性模型在三杆桁架中的应用,包括应力分析、平衡方程的求解以及不同阶段的材料行为,如弹性阶段、塑性阶段和卸载过程中的应力与位移计算。















 1118
1118

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










