1.3 加载路径对桁架的影响

个人专栏—塑性力学

1.1 塑性力学基本概念 塑性力学基本概念
1.2 弹塑性材料的三杆桁架分析 弹塑性材料的三杆桁架分析
1.3 加载路径对桁架的影响 加载路径对桁架的影响
2.1 塑性力学——应力分析基本概念 应力分析基本概念
2.2 塑性力学——主应力、主方向、不变量 主应力、主方向、不变量

---

---

$加载路径：$ 材料在受力时所经历的应力和应变变化路径。在塑性力学中，加载路径对材料的变形行为和力学性能有着重要影响。

$案例分析$

如图所示，理想弹塑性材料的三杆桁架受竖向力 $P$ 和水平力 $Q$的作用

由弹塑性力学分析可知：

$$\begin{array}{c}\text{平衡方程}\{\begin{array}{l}{\sigma }_2+\frac{\sqrt{2}({\sigma }_1+{\sigma }_3)}{2}=\frac{P}{A_0}\\ \frac{\sqrt{2}({\sigma }_1-{\sigma }_3)}{2}=\frac{Q}{A_0}\end{array}\\ \text{几何方程}\{\begin{array}{l}{\epsilon }_1=\frac{{\delta }_x}{2l_0}+\frac{{\delta }_y}{2l_0}\\ {\epsilon }_2=\frac{{\delta }_y}{l_0}\\ {\epsilon }_3=\frac{{\delta }_y}{2l_0}-\frac{{\delta }_x}{2l_0}\\ {\epsilon }_2={\epsilon }_1+{\epsilon }_3\end{array}\\ \text{理想弹塑性模型应力应变关系：}\\ \sigma =\{\begin{array}{ll}E\epsilon & (\epsilon \le {\epsilon }_s)\\ {\sigma }_s& (\epsilon \ge {\epsilon }_s)\end{array}\end{array}$$

$加载路径1$

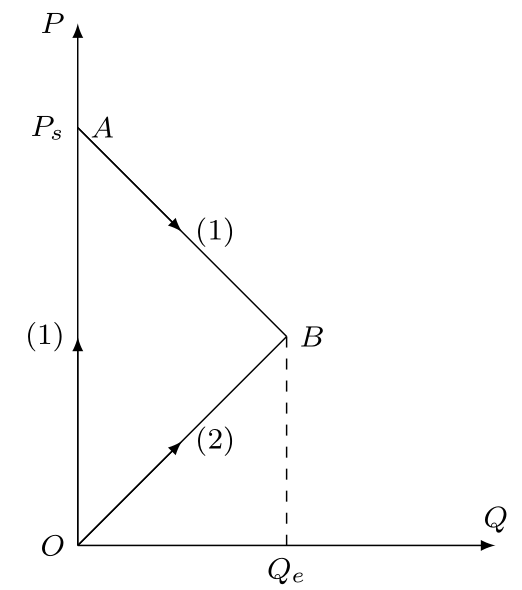
如图 $OA $所示，保持 $Q=0 $，加载 $P\rightarrow P_s(\sigma_sA_0(1+\sqrt{2})) $

$$\begin{array}{c}\text{可知杆内应力和节点位移}\\ \{\begin{array}{l}{\sigma }_1={\sigma }_2={\sigma }_3={\sigma }_s\\ {\delta }_y=2{\delta }_e={\delta }_s=\frac{2{\sigma }_s{l}_0}{E}\\ {\delta }_x=0\end{array}\\ \text{保持竖直位移 δy不变，增加 Q→Qs,由几何方程得}\\ \{\begin{array}{l}\Delta {\delta }_y=0,\Delta {\delta }_x={\delta }_x\ge 0\\ \Delta {\epsilon }_2=0\\ \Delta {\epsilon }_1=-\Delta {\epsilon }_3=\frac{\Delta {\delta }_x}{2l_0}\ge 0\end{array}\\ \text{由应变增量可知，当1杆继续伸长，2杆不变，3杆卸载}\\ \{\begin{array}{l}\Delta {\sigma }_1=\Delta {\sigma }_2=0\\ \Delta {\sigma }_3=E\Delta {\epsilon }_3=-E{\delta }_x/2l_0\le 0\end{array}\\ \text{由增量形式平衡方程可知}\\ \{\begin{array}{l}\Delta {\sigma }_2+\frac{\sqrt{2}(\Delta {\sigma }_1+\Delta {\sigma }_3)}{2}=\frac{\Delta P}{A_0}\\ \frac{\sqrt{2}(\Delta {\sigma }_1-\Delta {\sigma }_3)}{2}=\frac{\Delta Q}{A_0}\end{array}\\ \to \{\begin{array}{l}\frac{\Delta P}{A_0}=\frac{\Delta {\sigma }_3}{\sqrt{2}}\le 0\\ \frac{\Delta Q}{A_0}=-\frac{\Delta {\sigma }_3}{\sqrt{2}}\ge 0\end{array}\to \Delta P=-\Delta Q\end{array}$$

为保持 $\delta_y $不变， $Q $增加时 $P $必须减小，如图 $AB $段所示。

当 $\Delta \sigma_3=-2\sigma_s, \sigma_3=-\sigma_s $，3杆进入反向屈服,整个桁架进入塑性流动状态，此时 $Q $不再增加

$$\begin{array}{c}\{\begin{array}{l}Q=Q_s=\Delta Q=\sqrt{2}{\sigma }_s{A}_0\\ P=\Delta P+P_s=-\sqrt{2}{\sigma }_s{A}_0+{\sigma }_s{A}_0(1+\sqrt{2})={\sigma }_s{A}_0\end{array}\\ \text{桁架应力}{\sigma }_1={\sigma }_2={\sigma }_s,{\sigma }_3=-{\sigma }_s\\ \text{结合}\Delta {\sigma }_3=-2{\sigma }_s\text{可得节点位移:}\\ {\delta }_y={\delta }_s,{\delta }_x=\Delta {\delta }_x=\frac{4{\sigma }_s{l}_0}{E}=2{\delta }_s\\ \text{由几何方程可求得应变:}\\ {\epsilon }_1=3{\epsilon }_s,{\epsilon }_2=2{\epsilon }_s,{\epsilon }_3=-{\epsilon }_s\end{array}$$

$加载路径2$

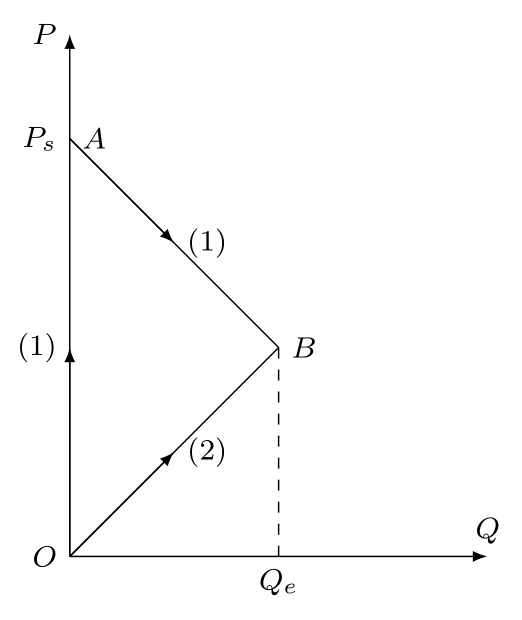
比例加载 $P:Q=1:\sqrt{2} $,直到桁架达到塑性极限状态，即 $P=\sigma_sA_0,Q=\sqrt{2}\sigma_sA_0 $,如图中路径 $OB $段所示。

弹性阶段由几何方程和平衡方程可知

$$\begin{array}{c}{\epsilon }_2={\epsilon }_1+{\epsilon }_3\\ {\sigma }_2={\sigma }_1+{\sigma }_3\\ \text{将 Q=2 P代入平衡方程可得3个杆的应力}\\ \{\begin{array}{l}{\sigma }_1=\frac{P}{2A_0}(\frac{\sqrt{2}}{1+\sqrt{2}}+2)\ge 0\\ {\sigma }_2=\frac{P}{A_0}\frac{\sqrt{2}}{1+\sqrt{2}}\ge 0\\ {\sigma }_3=\frac{P}{2A_0}(\frac{\sqrt{2}}{1+\sqrt{2}}-2)\le 0\end{array}\end{array}$$

三者中 $\sigma_1 $最大，当 $\sigma_1=\sigma_s $时，桁架达到弹性极限状态

$$\begin{array}{c}\{\begin{array}{l}{P}_e={\sigma }_s{A}_0\frac{2(1+\sqrt{2})}{2+3\sqrt{2}}\\ {\sigma }_1^e={\sigma }_s,{\epsilon }_1^e=\frac{{\sigma }_1^e}{E}={\epsilon }_s\\ {\sigma }_2^e=\frac{2\sqrt{2}}{2+3\sqrt{2}}{\sigma }_s,{\epsilon }_2^e=\frac{{\sigma }_2^e}{E}\\ {\sigma }_3^e=-\frac{2+2\sqrt{2}}{2+3\sqrt{2}}{\sigma }_s,{\epsilon }_3^e=\frac{{\sigma }_3^e}{E}\end{array}\{\begin{array}{l}{\delta }_x^e=\frac{2+2\sqrt{2}}{2+3\sqrt{2}}{\delta }_e\\ {\delta }_y^e=\frac{2\sqrt{2}}{2+3\sqrt{2}}{\delta }_e\end{array}\\ \text{继续加载，1杆屈服}\Delta {\sigma }_1=0,\Delta Q=\sqrt{2}\Delta P\\ \text{由增量式平衡方程可知}\\ \{\begin{array}{l}\Delta {\sigma }_2+\frac{\sqrt{2}(\Delta {\sigma }_1+\Delta {\sigma }_3)}{2}=\frac{\Delta P}{A_0}\\ \frac{\sqrt{2}(\Delta {\sigma }_1-\Delta {\sigma }_3)}{2}=\frac{\Delta Q}{A_0}\end{array}\to \{\begin{array}{l}\Delta {\sigma }_3=-\frac{2\Delta P}{A_0}\le 0\\ \Delta {\sigma }_2=\frac{(1+\sqrt{2})\Delta P}{A_0}\ge 0\end{array}\\ {\sigma }_1={\sigma }_s,{\sigma }_2={\sigma }_2^e+\Delta {\sigma }_2,{\sigma }_3={\sigma }_3^e+\Delta {\sigma }_3\\ \text{当 σ2=σs时，}\Delta {\sigma }_2={\sigma }_s-{\sigma }_2^e\\ \Delta P={\sigma }_s{A}_0\frac{\sqrt{2}}{2+3\sqrt{2}}\to \Delta {\sigma }_3=-\frac{2\sqrt{2}{\sigma }_s}{2+3\sqrt{2}}\\ {\sigma }_3={\sigma }_3^e+\delta {\sigma }_3=-{\sigma }_s\text{即桁架进入塑性状态}\\ \text{极限荷载为}P=P_e+\Delta P={\sigma }_s{A}_{0}Q=\sqrt{2}{\sigma }_s{A}_0=Q_s\\ \to \text{极限荷载不因加载路径的不同而改变}\\ \Delta {\epsilon }_2=\frac{\Delta {\sigma }_2}{E}=(1+\sqrt{2})\frac{\Delta P}{A_{0}E},\Delta {\epsilon }_3=\frac{\Delta {\sigma }_3}{E}=-\frac{2\Delta P}{A_{0}E}\\ \Delta {\delta }_x=(\Delta {\epsilon }_2-2\Delta {\epsilon }_3)l_0,\Delta {\delta }_y=\Delta {\epsilon }_2{l}_0\\ \to {\delta }_x=3{\delta }_e,{\delta }_y={\delta }_e,{\epsilon }_1=2{\epsilon }_s,{\epsilon }_2=-{\epsilon }_3={\epsilon }_s\end{array}$$

比较两种不同加载路径达到统一塑性极限载荷时，所得杆件中应力相同，但应变和位移不同。对于更复杂的静不定结构，更复杂的加载路径，结构内的应力分布也可能不同。

塑性问题不同于弹性问题的一个重要特点是: 当物体和结构发生塑性变形时，其应力、应变和位移依赖于外载的终值和加载历史。

如果你喜欢以上内容，或者对此感兴趣，欢迎一键三连，博主将持续更新，如果有任何问题，可以咨询博主，非常乐意为大家解答。