个人专栏—塑性力学
1.1 塑性力学基本概念 塑性力学基本概念
1.2 弹塑性材料的三杆桁架分析 弹塑性材料的三杆桁架分析
1.3 加载路径对桁架的影响 加载路径对桁架的影响
2.1 塑性力学——应力分析基本概念 应力分析基本概念
2.2 塑性力学——主应力、主方向、不变量 主应力、主方向、不变量
L o d e 参数简介 \color{blue}Lode参数简介 Lode参数简介
-
Lode参数是一种用于描述材料在多轴状态下的塑性行为的参数,可以准确描述材料的塑性变形特性。
-
Lode参数不能表示一点的应力状态,因为它不表示应力球张量
-
Lode参数$\mu_{\sigma} $ 反映受力状态的形式,即主应力之间的比例关系。
-
Lode参数的理论推导
在 σ − τ \sigma-\tau σ−τ平面上以 P 1 ( σ 1 , 0 ) , P 2 ( σ 2 , 0 ) , P 3 ( σ 3 , 0 ) P_1(\sigma_1,0),P_2(\sigma_2,0),P_3(\sigma_3,0) P1(σ1,0),P2(σ2,0),P3(σ3,0)三点中任意两点为直径作出三个摩尔圆
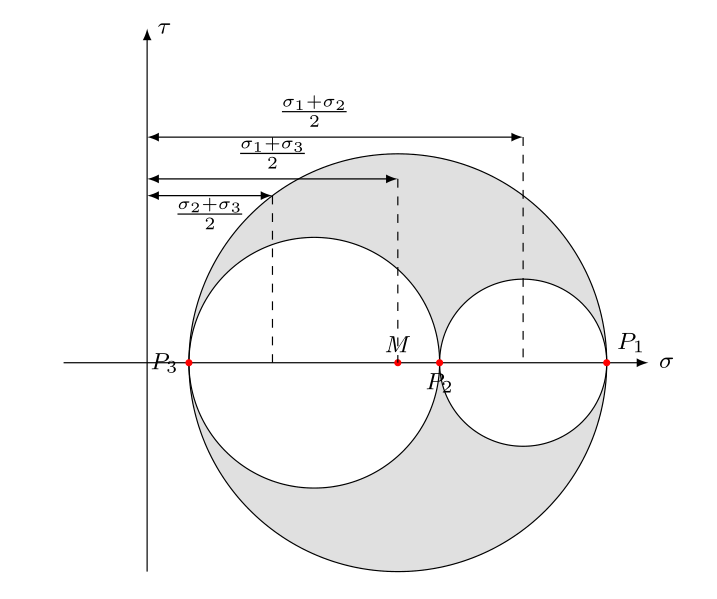
根据摩尔圆可得
1
2
P
1
P
3
=
1
2
(
σ
1
−
σ
3
)
=
τ
1
1
2
P
1
P
2
=
1
2
(
σ
1
−
σ
2
)
=
τ
2
2
3
P
1
P
3
=
1
2
(
σ
2
−
σ
3
)
=
τ
3
\begin{gather*} \frac{1}{2}P_1P_3=\frac{1}{2}(\sigma_1-\sigma_3)=\tau_1\\ \frac{1}{2}P_1P_2=\frac{1}{2}(\sigma_1-\sigma_2)=\tau_2\\ \frac{2}{3}P_1P_3=\frac{1}{2}(\sigma_2-\sigma_3)=\tau_3 \end{gather*}
21P1P3=21(σ1−σ3)=τ121P1P2=21(σ1−σ2)=τ232P1P3=21(σ2−σ3)=τ3
为考察中间应力
σ
2
\sigma_2
σ2对屈服的影响,可用
M
P
2
MP_2
MP2与
M
P
1
MP_1
MP1之比确定
P
2
P_2
P2在
P
1
P_1
P1与
P
3
P_3
P3之间的相对位置
μ
σ
=
M
P
2
M
P
1
=
P
2
P
3
−
M
P
3
M
P
1
=
2
σ
2
−
σ
3
σ
1
−
σ
3
−
1
\begin{align*} \mu_{\sigma}&=\frac{MP_2}{MP_1}\\ &=\frac{P_2P_3-MP_3}{MP_1}=2\frac{\sigma_2-\sigma_3}{\sigma_1-\sigma_3}-1 \end{align*}
μσ=MP1MP2=MP1P2P3−MP3=2σ1−σ3σ2−σ3−1
-
设主次序为 $\sigma_1\geq \sigma_2 \geq \sigma_3 $
-
单轴拉伸: $\sigma_1>0,\sigma_2=\sigma_3=0,\mu_{\sigma}=-1 $
-
纯剪切:$\sigma_1=-\sigma_3>0,\sigma_2=0,\mu_{\sigma}=0 $
-
单向压缩:$\sigma_1=\sigma_2=0,\sigma_3<0,\mu_{\sigma}=-1 $
-
-
偏张量三个不变量的比值:
S 1 : S 2 : S 3 = − 3 + μ σ : − 2 μ σ : 3 + μ σ S_1:S_2:S_3=-3+\mu_{\sigma}:-2\mu_{\sigma}:3+\mu_{\sigma} S1:S2:S3=−3+μσ:−2μσ:3+μσ -
如图,将坐标原点 $O $移到新的位置 $O^{'} $,则
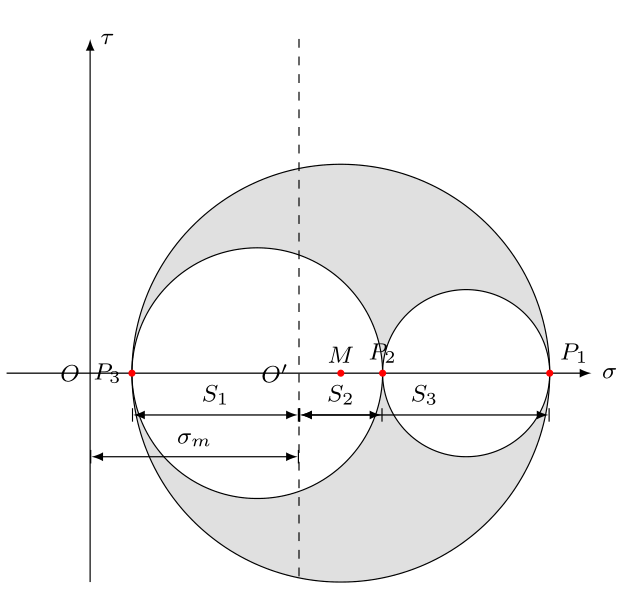
O O ′ = σ 1 + σ 2 + σ 3 3 = σ m O ′ P 1 = σ 1 − σ m = S 1 O ′ P 2 = σ 2 − σ m = S 2 O ′ P 3 = σ 3 − σ m = S 3 \begin{align*} OO^{'}&=\frac{\sigma_1+\sigma_2+\sigma_3}{3}=\sigma_m\\ O^{'}P_1&=\sigma_1-\sigma_m=S_1\\ O^{'}P_2&=\sigma_2-\sigma_m=S_2\\ O^{'}P_3&=\sigma_3-\sigma_m=S_3 \end{align*} OO′O′P1O′P2O′P3=3σ1+σ2+σ3=σm=σ1−σm=S1=σ2−σm=S2=σ3−σm=S3
-
由此所得轴平移后应力圆即是描述应力偏量的应力圆。
-
原点任意平移一个距离,相当于在原有应力状态下叠加一个静水压力,这个叠加不影响屈服函数和塑性变形。
-
可见 $\mu_{\sigma} $是描述应力偏量的特征值,它与应力偏量不变量 $J_2,J_3 $有关,而与应力球张量无关。
应力空间 \color{blue}应力空间 应力空间
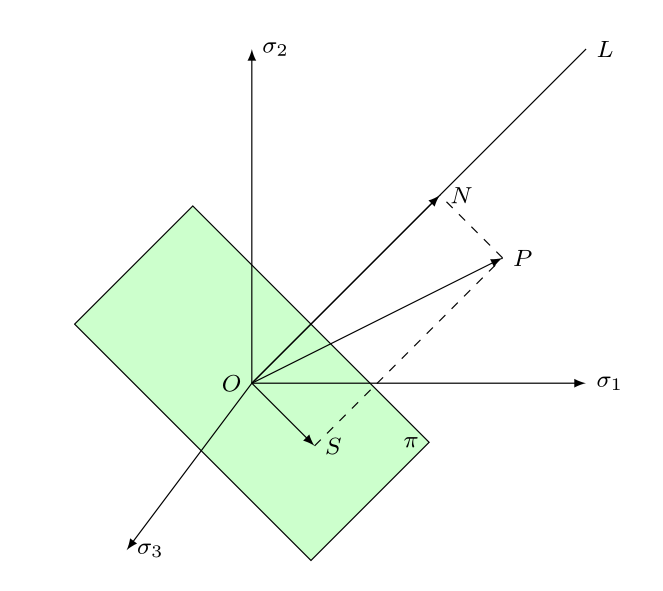
如图所示
-
L直线:主应力空间中过原点并与坐标轴成等角的直线
l 1 = l 2 = l 3 = 3 3 σ 1 = σ 2 = σ 3 l_1=l_2=l_3=\frac{\sqrt{3}}{3}\quad \sigma_1=\sigma_2=\sigma_3 l1=l2=l3=33σ1=σ2=σ3
L直线上的点代表应力球张量点的状态,偏张量为0,不产生塑性变形。 -
π \pi π平面:通过主应力空间原点,与L直线垂直的平面,其控制方程为:
σ
1
+
σ
2
+
σ
3
=
0
\sigma_1+\sigma_2+\sigma_3=0
σ1+σ2+σ3=0
$\pi $平面上点的平均应力为0,该平面上的点只有应力偏张量,不引起体积变形。
-
O P ⃗ = O S ⃗ + O N ⃗ \vec{OP}=\vec{OS}+\vec{ON} OP=OS+ON $ON $沿L直线, $OS $在 $\pi $平面
-
以三个相互垂直的单位向量 $i_1,i_2,i_3 $作为主应力空间中的基向量,构建与 $\pi $平面重合的斜面,基向量 $(i_1,i_2,i_3) $在 斜平面上的投影记为 $(i_1{'},i_2{‘},i_3^{’}) $
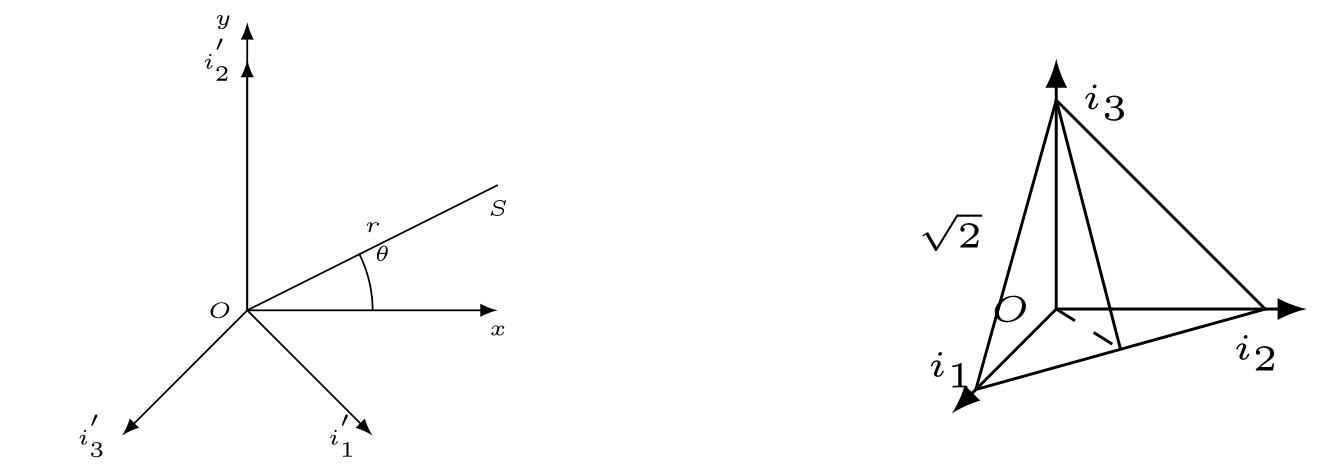
由几何关系可知 $i_{\alpha}^{'} $与 $i_{\alpha} $之间夹角满足 $ \cos\beta=\sqrt{\frac{2}{3}}$
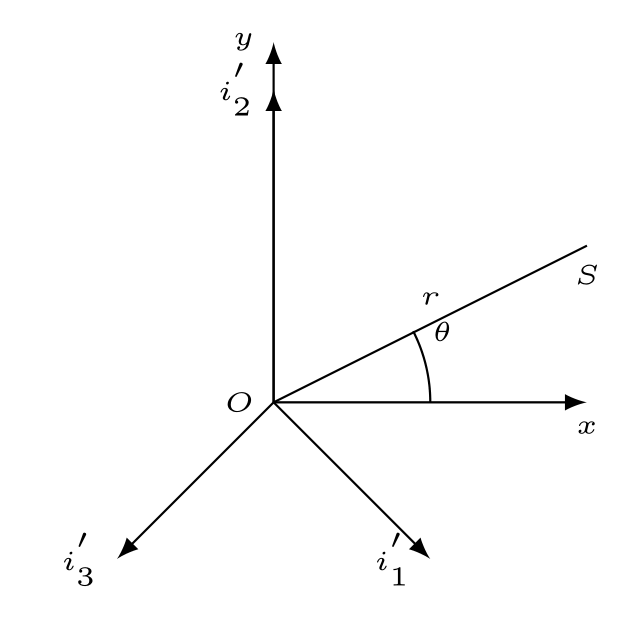
$S_1i_1,S_2i_2,S_3i_3 $投影到 $\pi $平面上时,可得到它们的 $(x,y) $坐标
( 3 2 S 1 cos β , − 1 2 S 1 cos β ) ( 0 , S 2 cos β ) ( − 3 2 S 3 cos β , − 1 2 S 3 cos β ) (\frac{\sqrt{3}}{2}S_1\cos\beta,-\frac{1}{2}S_1\cos\beta)\quad (0,S_2\cos\beta)\quad (-\frac{\sqrt{3}}{2}S_3\cos\beta,-\frac{1}{2}S_3\cos\beta) (23S1cosβ,−21S1cosβ)(0,S2cosβ)(−23S3cosβ,−21S3cosβ)
- $OS $在 $\pi $平面上的坐标可写为
{
x
=
2
2
(
S
1
−
S
3
)
=
2
2
(
σ
1
−
σ
3
)
y
=
6
6
(
2
S
2
−
S
1
−
S
3
)
=
6
6
(
2
σ
2
−
σ
1
−
σ
3
)
\begin{cases} x=\frac{\sqrt{2}}{2}(S_1-S_3)=\frac{\sqrt{2}}{2}(\sigma_1-\sigma_3)\\ y=\frac{\sqrt{6}}{6}(2S_2-S_1-S_3)=\frac{\sqrt{6}}{6}(2\sigma_2-\sigma_1-\sigma_3) \end{cases}
{x=22(S1−S3)=22(σ1−σ3)y=66(2S2−S1−S3)=66(2σ2−σ1−σ3)
采用极坐标表示为
{
r
=
1
2
(
σ
1
−
σ
3
)
2
+
1
6
(
2
σ
2
−
σ
1
−
σ
3
)
2
=
2
J
2
′
tan
θ
=
3
3
2
σ
2
−
σ
1
−
σ
3
σ
1
−
σ
3
=
3
3
μ
σ
\begin{cases} r=\sqrt{\frac{1}{2}(\sigma_1-\sigma_3)^2+\frac{1}{6}(2\sigma_2-\sigma_1-\sigma_3)^2}=\sqrt{2J_2^{'}}\\ \tan \theta=\frac{\sqrt{3}}{3}\frac{2\sigma_2-\sigma_1-\sigma_3}{\sigma_1-\sigma_3}=\frac{\sqrt{3}}{3}\mu_{\sigma} \end{cases}
{r=21(σ1−σ3)2+61(2σ2−σ1−σ3)2=2J2′tanθ=33σ1−σ32σ2−σ1−σ3=33μσ
$-30^{\circ}\leq \theta \leq 30^{\circ} $
- 偏应力不变量在
π
\pi
π平面的投影表示
S 2 = − ( S 1 + S 3 ) S 1 − S 3 = 2 x = 2 r cos θ S 1 + S 3 = − 2 3 y = − 2 3 r sin θ → { S 1 = 2 2 x − 6 6 y = 2 3 r sin ( θ + 2 π 3 ) S 2 = 2 3 y = 2 3 r sin θ S 3 = − 2 2 x − 6 6 y = 2 3 r sin ( θ − 2 π 3 ) \begin{gather*} S_2=-(S_1+S_3)\\ S_1-S_3=\sqrt{2}x=\sqrt{2}r\cos\theta\\ S_1+S_3=-\sqrt{\frac{2}{3}}y=-\sqrt{\frac{2}{3}}r\sin\theta\\ \to \begin{cases} S_1=\frac{\sqrt{2}}{2}x-\frac{\sqrt{6}}{6}y=\sqrt{\frac{2}{3}}r\sin(\theta+\frac{2\pi}{3})\\ S_2=\sqrt{\frac{2}{3}}y=\sqrt{\frac{2}{3}}r\sin\theta\\ S_3=-\frac{\sqrt{2}}{2}x-\frac{\sqrt{6}}{6}y=\sqrt{\frac{2}{3}}r\sin(\theta-\frac{2\pi}{3}) \end{cases} \end{gather*} S2=−(S1+S3)S1−S3=2x=2rcosθS1+S3=−32y=−32rsinθ→⎩ ⎨ ⎧S1=22x−66y=32rsin(θ+32π)S2=32y=32rsinθS3=−22x−66y=32rsin(θ−32π)
























 964
964

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










