数字信号处理基础：采样、混叠现象与抗混叠滤波器设计注意事项

引言

一、基础概念的建立

1. 采样过程
定义：在等间隔时间点上测量连续信号的幅度。
目的：将模拟信号转换为数字信号，便于数字系统处理。

2. 采样信号
表示：采样信号可以表示为一系列脉冲或样本点。
特性：采样信号的周期性由采样频率决定。

3. 奈奎斯特定理

• 定理：为了能够无失真地从数字信号中恢复原始地模拟信号，采样频率必须至少是信号最高频率地两倍。这个最低地采样频率为奈奎斯特频率。

4. 奈奎斯特频率（$f_N$）

• 定义奈奎斯特频率是采样频率($f_S$)的一半，用公式表示为$f_N=\frac{f_S}{2}$，它定义了一个理论上的界限，即信号中可被无失真重建信号的最高频率。如果原始模拟信号的所有频率分量都低于或等于（$f_N$），那么通过采样得到的数字信号可以被完整地重建出。

5.理解混叠现象

• 定义：当信号频率高于采样率的两倍时，信号的高频成份会在采样后出现在低频区域，导致信号失真。

• 解析：设$f_{max}$为模拟信号的最大频率，$f_S$为ADC采样率 ，则有$f_S$<$2f_{max}$，可推出$\frac{f_S}{2}=f_N<f_{max}$，即信号的最大频率或或信号的高频分量超过奈奎斯特频率$f_N$时，超出的部分在频域中的位置通过镜像方式折叠到低频部分。

• 生活示例：眼睛观察快速旋转的车轮或风扇时，如果采样率（即眼睛更新图像的速率）不够高，可能会看到车轮旋转速度减慢或反向旋转。

二、混叠信号示例讲解

当ADC输入信号一个900kHz的正弦波，且ADC的采样率为1MHz时，根据混叠现象的定义，ADC将产生混叠效应。下图为时域下图，红色为输入波形，蓝色为混叠信号，其频率为100kHz。

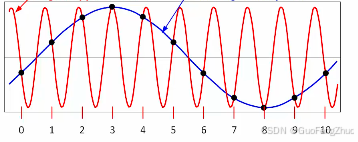
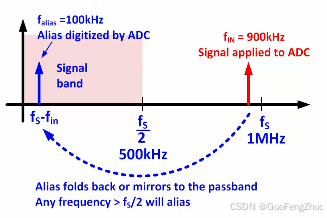
为了更好的理解混叠现象，我们需要从频域的维度来分析分析，奈奎斯特频率$\frac{f_S}{2}=f_N=500kHz$,$f_{in}=900kHz$，满足混叠条件$f_N<f_{in}$,则与$f_N$为中心轴对$f_{in}$进行镜像或折叠，镜像或折叠后的频率为$f_S-f_{in}=100kHz$,即如果对波形进行复原，你将看到的是100kHz的蓝色波形。.

从0到$f_N$区域称其为第一个奈奎斯区域，从$f_N$到$f_S$ 称其为第二个奈斯区域。实际上，根据傅里叶变换，采样信号的频谱会在采样频率$f_S$的整数倍除重复出现，形成周期性频谱，例如，采样频谱会在$f_S$，$f_{2S}$，$f_{3S}$…等频率上重复。相应地，奈奎斯区域也是周期镜像或重叠，详细见下图。

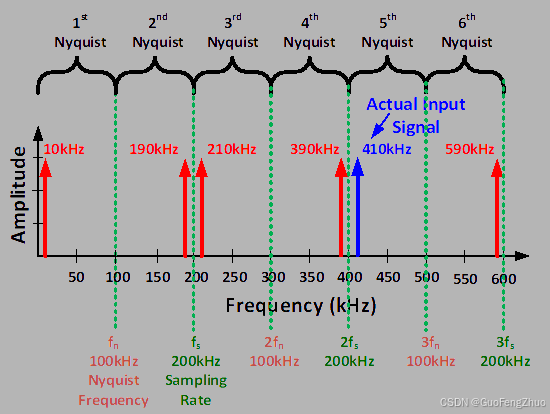
以前面的示例为例，其前六个奈奎斯区域对应的混叠频率如下表：

奈奎斯区域	混叠频率
1st Nyquist Zone	100kHZ
2nd Nyquist Zone	900kHZ
3rd Nyquist Zone	1.1MHZ
4th Nyquist Zone	1.9MHZ
5th Nyquist Zone	2.1MHZ
6th Nyquist Zone	2.9MHZ

当然，设计时，我们只关注第一个奈奎斯特区域的混叠情况。

三、抗混叠滤波器的设计

3.1.目的：

• 降低混叠效应，确保信号在采样前已经被过滤，只包含低于奈奎斯特频率的频率分量。

3.2. 设计考量点：

• 在模拟到数字的转换过程中，量化精度主要取决于模数转换器（A/D转换器）的分辨率。量化误差，表现为数字值与模拟值之间的差异，通常用最低有效位（LSB）来量化。量化误差的典型范围是每个数字位±0.5LSB。
  设计抗混叠滤波器时，核心目标是将噪声信号的振幅降至ADC的检测极限之下，即小于ADC的LSB的一半。这要求滤波器在设计时必须考虑通带宽度、截止频率和衰减率。截止频率定义了信号的通带范围，而衰减率则决定了阻带的宽度和深度，对于混叠信号的有效抑制至关重要。建议至少采用2阶滤波器设计，以确保足够的衰减性能。
  
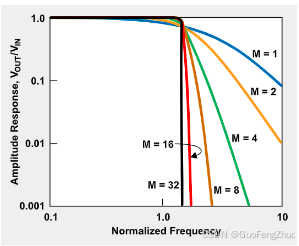
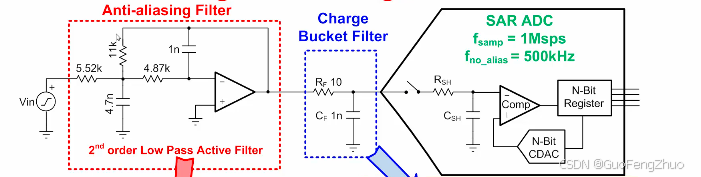
  值得注意的是，ADC前端的RC电路主要用于在ADC内部采样保持电路切换时提供瞬时能量，并非用于抗混叠。这一点在设计抗混叠滤波器时应予以明确区分，以避免对RC电路功能的误解和不当应用。

​

​