前言
本博客总结的是吴恩达深度学习全192讲哔哩哔哩
为了方便理解 和回顾写下本笔记
标题对应相应视频编号
2.1二元分类(猫)
给定一张64*64的图片
设x为 列向量 存储图片RGB数据
x = [ 255 255 ⋮ 255 255 ⋮ 255 255 ⋮ ] x=\begin{bmatrix} 255\\ 255\\ \vdots\\ 255\\ 255\\ \vdots\\ 255\\ 255\\ \vdots \end{bmatrix}\quad x= 255255⋮255255⋮255255⋮ 分别对应 红绿蓝 列向量维度nx=64*64*3
设(x,y) x ∈ R n x ( x 是 n 维向量 ) y ∈ [ 0 , 1 ] \quad x\in R^{nx} (x是n维向量)\quad y\in [0,1]\quad x∈Rnx(x是n维向量)y∈[0,1]为一个训练集样本
设m是训练集样本总数
训练集:
[
(
x
(
1
)
,
y
(
1
)
)
,
(
x
(
2
)
,
y
(
2
)
)
,
⋯
,
(
x
(
m
)
,
y
(
m
)
)
]
[(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),\cdots,(x^{(m)},y^{(m)})]
[(x(1),y(1)),(x(2),y(2)),⋯,(x(m),y(m))]
其中
(
x
(
i
)
,
y
(
i
)
)
(x^{(i)},y^{(i)})
(x(i),y(i))表示第i个样本
设
X
=
[
∣
∣
∣
x
(
1
)
⋯
x
(
m
)
∣
∣
∣
]
(
2.1.1
)
X=\begin{bmatrix} | & | &| \\ x^{(1)} &\cdots &x^{(m)} \\ | &| &| \end{bmatrix} \quad (2.1.1)
X=
∣x(1)∣∣⋯∣∣x(m)∣
(2.1.1)
因为 x为列向量 所以X为(nx,m)矩阵 nx行 m列
设
Y
=
[
∣
∣
∣
y
(
1
)
⋯
y
(
3
)
∣
∣
∣
]
(
2.1.2
)
Y = \begin{bmatrix} | & | & | & \\ y^{(1)} & \cdots & y^{(3)}\\ | & | & | \end{bmatrix} \ (2.1.2)
Y=
∣y(1)∣∣⋯∣∣y(3)∣
(2.1.2)
此处
y
(
i
)
y^{(i)}
y(i)是一个数 当然也是列向量,Y为(1,m)矩阵,Y.shape=(1,m)
tips:把数或列向量 按列排列很有用(排成行)
2.2 逻辑回归
给定x 算 y ^ = P ( y = 1 ∣ x ) 0 ≤ y ^ ≤ 1 \hat{y}=P(y=1|x) \quad 0 \leq \hat{y} \leq 1 y^=P(y=1∣x)0≤y^≤1
设
y
^
=
σ
(
w
T
x
+
b
)
\hat{y}= \sigma(w^Tx+b)
y^=σ(wTx+b)
这里
σ
\sigma
σ是sigmoid激活函数 看博客sigmoid函数
参数:
w
∈
R
(
n
x
)
w \in R^{(nx)} \quad
w∈R(nx) w是nx维向量
损失函数
对训练集 [ ( x ( 1 ) , y ( 1 ) ) , ( x ( 2 ) , y ( 2 ) ) , ⋯ , ( x ( m ) , y ( m ) ) ] [(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),\cdots,(x^{(m)},y^{(m)})] [(x(1),y(1)),(x(2),y(2)),⋯,(x(m),y(m))]
设损失函数loss fuction:
L
(
y
^
,
y
)
=
−
(
y
l
o
g
y
^
+
(
1
−
y
)
l
o
g
(
1
−
y
^
)
)
L(\hat{y},y)=-(ylog \hat{y}+(1-y)log(1-\hat{y}))
L(y^,y)=−(ylogy^+(1−y)log(1−y^))
loss fuction有意义原因:y=1 y=0
设代价函数cost function: J ( w , b ) = 1 m ∑ i = 1 m L ( y ( i ) , y ) J(w,b)=\frac{1}{m} \sum_{i=1}^m L(y^{(i)},y) J(w,b)=m1∑i=1mL(y(i),y)
2.4梯度下降
w
:
=
w
−
α
J
(
w
)
d
w
w:=w - \alpha \frac{J(w)}{dw}
w:=w−αdwJ(w)
说明为啥迭代接近最优
w
:
=
w
−
α
α
(
J
(
w
,
b
)
)
α
(
w
)
w:=w - \alpha \frac{\alpha(J(w,b))}{\alpha (w)}\quad
w:=w−αα(w)α(J(w,b))
偏导数写法不影响
2.9逻辑回归梯度下降(一个样本)
给定一个样本(x,y)
假设w,x为二维向量 nx=2
x
=
[
x
1
x
2
]
w
=
[
w
1
w
2
]
x= \begin{bmatrix} x1\\ x2 \end{bmatrix}\quad w= \begin{bmatrix} w1\\ w2 \end{bmatrix}
x=[x1x2]w=[w1w2]
x1,x2,w1,w2分别是一个数
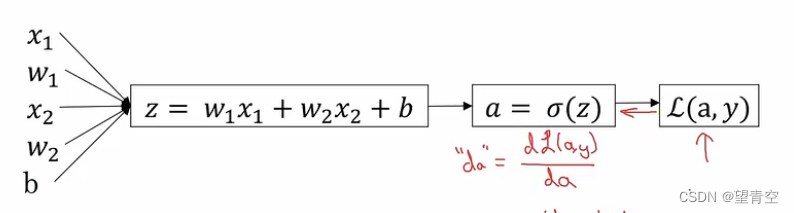
设
z
=
w
T
x
+
b
y
^
=
a
=
σ
(
z
)
]
z
=
w
1
x
1
+
w
2
x
2
+
b
L
(
a
,
y
)
d
a
=
d
L
(
a
,
y
)
d
a
d
z
=
d
L
d
z
=
d
L
(
a
,
y
)
d
a
⋅
d
a
d
z
=
a
−
y
d
w
1
=
α
L
α
w
1
=
x
1
⋅
d
z
d
w
2
=
x
2
⋅
d
z
d
b
=
d
z
(2.9.1)
\begin{aligned} &z=w^Tx+b \\ &\hat{y}=a=\sigma(z) ] \\ &z=w_1x_1+w_2x_2+b \\ &L(a,y) \\ &da=\frac{dL(a,y)}{da} \\ &dz=\frac{dL}{dz}=\frac{dL(a,y)}{da} \cdot \frac{da}{dz}=a-y \quad \\ &dw_1=\frac{\alpha L}{\alpha w_1}=x_1 \cdot dz \\ &dw_2=x_2 \cdot dz \\ &db=dz \end{aligned} \tag{2.9.1}
z=wTx+by^=a=σ(z)]z=w1x1+w2x2+bL(a,y)da=dadL(a,y)dz=dzdL=dadL(a,y)⋅dzda=a−ydw1=αw1αL=x1⋅dzdw2=x2⋅dzdb=dz(2.9.1)
链式求导,其中
d
a
d
z
=
a
(
1
−
a
)
详见
s
i
g
m
a
函数导数
)
\frac{da}{dz}=a(1-a)详见sigma函数导数)
dzda=a(1−a)详见sigma函数导数)
2.10 m个样本下的逻辑回归
设定有m个训练样本 w,x的维度仍是2维向量 参考标题2.9
样本
(
x
(
i
)
,
y
(
i
)
)
对应
z
(
i
)
a
(
i
)
x
1
(
i
)
x
2
(
i
)
d
w
1
(
i
)
d
w
2
(
i
)
(x^{(i)},y^{(i)})对应z^{(i)} \quad a^{(i)}\quad x_1^{(i)} \quad x_2^{(i)}\quad dw_1^{(i)} \quad dw_2^{(i)}
(x(i),y(i))对应z(i)a(i)x1(i)x2(i)dw1(i)dw2(i)
参数
w
1
w
2
b
在一次梯度下降中是固定的
w_1 \quad w_2 \quad b在一次梯度下降中是固定的
w1w2b在一次梯度下降中是固定的
J
(
w
,
b
)
=
1
m
∑
i
=
1
m
L
(
a
(
i
)
,
y
(
i
)
)
J(w,b)= \frac{1}{m} \sum_{i=1}^mL(a^{(i)},y^{(i)}) \\
J(w,b)=m1i=1∑mL(a(i),y(i))
设
d
w
1
=
1
m
∑
i
=
1
m
α
(
L
[
a
(
i
)
,
y
(
i
)
]
)
α
(
w
1
)
则
=
1
m
∑
i
=
1
m
d
w
1
(
i
)
=
1
m
∑
i
=
1
m
x
1
(
i
)
⋅
d
z
(
i
)
d
w
2
=
1
m
∑
i
=
1
m
α
(
L
[
a
(
i
)
,
y
(
i
)
]
)
α
(
w
2
)
则
=
1
m
∑
i
=
1
m
d
w
2
(
i
)
=
1
m
∑
i
=
1
m
x
2
(
i
)
⋅
d
z
(
i
)
(2.10.2)
\begin{aligned} dw_1 &= \frac{1}{m} \sum_{i=1}^m \frac{\alpha (L[a^{(i)},y^{(i)}])}{\alpha (w_1)}\\ 则&= \frac{1}{m} \sum_{i=1}^m dw_1^{(i)} \\ &= \frac{1}{m} \sum_{i=1}^{m}x_1^{(i)} \cdot dz^{(i)} \\ \\ dw_2 &= \frac{1}{m} \sum_{i=1}^m \frac{\alpha (L[a^{(i)},y^{(i)}])}{\alpha (w_2)}\\ 则&= \frac{1}{m} \sum_{i=1}^m dw_2^{(i)} \\ &= \frac{1}{m} \sum_{i=1}^{m}x_2^{(i)} \cdot dz^{(i)} \end{aligned} \tag{2.10.2}
dw1则dw2则=m1i=1∑mα(w1)α(L[a(i),y(i)])=m1i=1∑mdw1(i)=m1i=1∑mx1(i)⋅dz(i)=m1i=1∑mα(w2)α(L[a(i),y(i)])=m1i=1∑mdw2(i)=m1i=1∑mx2(i)⋅dz(i)(2.10.2)
推导见公式2.9.1
设
d
b
=
1
m
∑
i
=
1
m
α
(
L
[
a
(
i
)
,
y
(
i
)
]
)
α
(
b
)
则
=
1
m
∑
i
=
1
m
d
z
(
i
)
=
1
m
∑
i
=
1
m
a
(
i
)
−
y
(
i
)
(2.10.2)
\begin{aligned} db &= \frac{1}{m} \sum_{i=1}^m \frac{\alpha (L[a^{(i)},y^{(i)}])}{\alpha (b)}\\ 则&= \frac{1}{m} \sum_{i=1}^m dz^{(i)} \\ &=\frac{1}{m} \sum_{i=1}^ma^{(i)} - y^{(i)} \end{aligned} \tag{2.10.2}
db则=m1i=1∑mα(b)α(L[a(i),y(i)])=m1i=1∑mdz(i)=m1i=1∑ma(i)−y(i)(2.10.2)
推导见公式2.9.1
可以用一个for循环计算
d
w
1
d
w
2
d
b
dw_1 \quad dw_2 \quad db
dw1dw2db
然后计算出此次梯度下降得出的
w
1
w
2
b
w_1 \quad w_2 \quad b
w1w2b
w
1
=
w
1
−
α
⋅
d
w
1
w
2
=
w
2
−
α
⋅
d
w
2
b
=
b
−
α
⋅
d
b
\begin{aligned} &w_1= w_1- \alpha \cdot dw_1 \\ &w_2=w_2 - \alpha \cdot dw_2 \\ &b=b- \alpha \cdot db \end{aligned}
w1=w1−α⋅dw1w2=w2−α⋅dw2b=b−α⋅db
以上章节 w与x的维度nx=2,下一章扩展nx维度 并且采用向量化方法运算得出 d w 1 d w 2 d b dw_1 \quad dw_2 \quad db dw1dw2db
2.13向量化逻辑回归
设
z
=
w
T
x
+
b
z
,
b
∈
R
(实数)
w
=
[
w
1
⋮
w
n
x
]
x
=
[
x
1
⋮
x
n
x
]
x
,
w
∈
R
n
x
z=w^Tx+b \quad z,b\in R(实数)\\ w=\begin{bmatrix} w_1\\ \vdots \\ w_{nx} \end{bmatrix} \quad x=\begin{bmatrix} x_1\\ \vdots \\ x_{nx} \end{bmatrix} \quad x,w\in R^{nx}
z=wTx+bz,b∈R(实数)w=
w1⋮wnx
x=
x1⋮xnx
x,w∈Rnx
python中用一行代码运算
z
z
z: z=np.dot(w,x)+b
X
=
[
∣
∣
∣
x
(
1
)
⋯
x
(
2
)
∣
∣
∣
]
X=\begin{bmatrix} |&|&| \\ x^{(1)}&\cdots& x^{(2)} \\ |&|&| \end{bmatrix}
X=
∣x(1)∣∣⋯∣∣x(2)∣
X矩阵里的
x
(
i
)
x^{(i)}
x(i)为nx维列向量 详见(2.1.1)公式
设
Z
=
[
z
(
i
)
,
z
(
i
)
,
⋯
,
z
(
m
)
]
=
w
T
X
+
[
b
,
b
,
⋯
,
b
]
z
(
i
)
∈
R
Z
为
(
1
,
m
)
矩阵
\begin{aligned} &Z=\begin{bmatrix} z^{(i)},z^{(i)},\cdots,z^{(m)} \end{bmatrix}=w^TX+[b,b,\cdots,b] \\ &z^{(i)} \in R \quad Z为(1,m)矩阵 \end{aligned}
Z=[z(i),z(i),⋯,z(m)]=wTX+[b,b,⋯,b]z(i)∈RZ为(1,m)矩阵
python中用一行代码算
Z
Z
Z: Z=np.dot(w.T,X)+b
其中 b会被广播成[b,b,…,b] (1,m)矩阵
设
A
=
[
a
(
1
)
,
a
(
2
)
,
⋯
,
a
(
m
)
]
=
σ
(
Z
)
a
(
i
)
∈
R
A
是
(
1
,
m
)
矩阵
\begin{aligned} &A=\begin{bmatrix} a^{(1)},a^{(2)},\cdots,a^{(m)} \end{bmatrix}=\sigma(Z)\\ &a^{(i)} \in R \quad A是(1,m)矩阵 \end{aligned}
A=[a(1),a(2),⋯,a(m)]=σ(Z)a(i)∈RA是(1,m)矩阵
python中用一个函数就能算A
设
d
Z
=
[
d
z
(
i
)
,
d
z
(
i
)
,
⋯
,
d
z
(
m
)
]
其中
d
z
(
i
)
=
a
(
i
)
−
y
(
i
)
参考
(
2.9.1
)
\begin{aligned} &dZ=[dz^{(i)},dz^{(i)},\cdots,dz^{(m)}] \\ &其中dz^{(i)}=a^{(i)}-y^{(i)} \quad参考(2.9.1) \end{aligned}
dZ=[dz(i),dz(i),⋯,dz(m)]其中dz(i)=a(i)−y(i)参考(2.9.1)
设
Y
=
[
y
(
i
)
,
y
(
i
)
,
⋯
,
y
(
m
)
]
y
(
i
)
是一个数
\begin{aligned} &Y=[y^{(i)},y^{(i)},\cdots,y^{(m)}] \\ &y^{(i)}是一个数 \end{aligned}
Y=[y(i),y(i),⋯,y(m)]y(i)是一个数
向量化求变量
d
Z
=
A
−
Y
=
[
a
(
1
)
−
y
(
1
)
,
⋯
,
a
(
m
)
−
y
(
m
)
]
\begin{aligned} &dZ=A-Y=[a^{(1)}-y^{(1)},\cdots,a^{(m)}-y^{(m)}] \\ \end{aligned}
dZ=A−Y=[a(1)−y(1),⋯,a(m)−y(m)]
d
b
=
1
m
∑
i
=
1
m
d
z
(
i
)
=
1
m
∑
i
=
1
m
a
(
i
)
−
y
(
i
)
=
1
m
n
p
.
s
u
m
(
d
Z
)
\begin{aligned} db &= \frac{1}{m} \sum_{i=1}^m dz^{(i)} \\ &=\frac{1}{m} \sum_{i=1}^ma^{(i)} - y^{(i)} \\ &=\frac{1}{m}np.sum(dZ) \end{aligned}
db=m1i=1∑mdz(i)=m1i=1∑ma(i)−y(i)=m1np.sum(dZ)
设
d
W
=
[
d
w
1
d
w
2
⋮
d
w
n
x
]
=
[
1
m
∑
i
=
1
m
x
1
(
i
)
⋅
d
z
(
i
)
1
m
∑
i
=
1
m
x
2
(
i
)
⋅
d
z
(
i
)
⋮
1
m
∑
i
=
1
m
x
n
x
(
i
)
⋅
d
z
(
i
)
]
其中
d
w
i
∈
R
参考
(
2.10.2
)
\begin{aligned} dW=\begin{bmatrix} dw_1\\dw_2\\ \vdots \\ dw_{nx} \\ \end{bmatrix}=\begin{bmatrix} \frac{1}{m} \sum_{i=1}^{m}x_1^{(i)} \cdot dz^{(i)} \\ \frac{1}{m} \sum_{i=1}^{m}x_2^{(i)} \cdot dz^{(i)} \\ \vdots \\ \frac{1}{m} \sum_{i=1}^{m}x_{nx}^{(i)} \cdot dz^{(i)} \\ \end{bmatrix}\\ 其中dw_i \in R \quad参考(2.10.2)\\ \end{aligned}
dW=
dw1dw2⋮dwnx
=
m1∑i=1mx1(i)⋅dz(i)m1∑i=1mx2(i)⋅dz(i)⋮m1∑i=1mxnx(i)⋅dz(i)
其中dwi∈R参考(2.10.2)
d
W
=
1
m
X
⋅
d
Z
T
=
[
∣
∣
∣
x
(
1
)
⋯
x
(
2
)
∣
∣
∣
]
⋅
[
d
z
(
1
)
d
z
(
2
)
⋮
d
z
(
m
)
]
=
(
n
x
,
m
)
⋅
(
m
,
1
)
=
[
1
m
∑
i
=
1
m
x
1
(
i
)
⋅
d
z
(
i
)
1
m
∑
i
=
1
m
x
2
(
i
)
⋅
d
z
(
i
)
⋮
1
m
∑
i
=
1
m
x
n
x
(
i
)
⋅
d
z
(
i
)
]
=
[
d
w
1
d
w
2
⋮
d
w
n
x
]
\begin{aligned} dW & =\frac{1}{m}X \cdot dZ^T \\ &=\begin{bmatrix} |&|&| \\ x^{(1)}&\cdots& x^{(2)} \\ |&|&| \end{bmatrix} \cdot \begin{bmatrix} dz^{(1)}\\dz^{(2)}\\ \vdots\\ dz^{(m)} \end{bmatrix} \\ &=(nx,m) \cdot (m,1) \\ &=\begin{bmatrix} \frac{1}{m} \sum_{i=1}^{m}x_1^{(i)} \cdot dz^{(i)} \\ \frac{1}{m} \sum_{i=1}^{m}x_2^{(i)} \cdot dz^{(i)} \\ \vdots \\ \frac{1}{m} \sum_{i=1}^{m}x_{nx}^{(i)} \cdot dz^{(i)} \\ \end{bmatrix}=\begin{bmatrix} dw_1\\dw_2\\ \vdots \\ dw_{nx} \\ \end{bmatrix} \end{aligned}
dW=m1X⋅dZT=
∣x(1)∣∣⋯∣∣x(2)∣
⋅
dz(1)dz(2)⋮dz(m)
=(nx,m)⋅(m,1)=
m1∑i=1mx1(i)⋅dz(i)m1∑i=1mx2(i)⋅dz(i)⋮m1∑i=1mxnx(i)⋅dz(i)
=
dw1dw2⋮dwnx






















 53
53











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








