【线性代数公开课MIT Linear Algebra】 第二十四课 特征值与特征向量的应用——马尔科夫矩阵、傅里叶级数

本系列笔记为方便日后自己查阅而写，更多的是个人见解，也算一种学习的复习与总结，望善始善终吧~

马尔科夫矩阵Markov Matrix

马尔科夫矩阵Markov Matrix有两个性质：所有元素大于等于0，所有矩阵的列相加等于1。

这里性质导致一些有趣的特性：

• 马尔科夫矩阵Markov Matrix 的幂依然是马尔科夫矩阵Markov Matrix
• 马尔科夫矩阵Markov Matrix的其中一个特征值为1，其他所有的特征值的绝对值小于1

这二个特性导致了什么呢？看看我们之前关于矩阵的幂的公式：

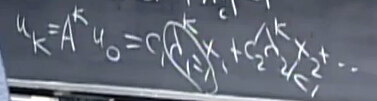
不难发现随着k的增大，特征值的绝对值小于1的项最终都趋近于0，steady state取决于特征值为1的那一项。那么特征向量呢？
一个例子：

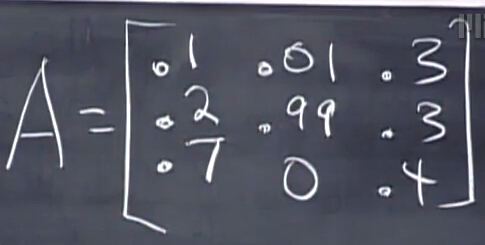
既然我们说其必定存在特征值为1，那么观察：

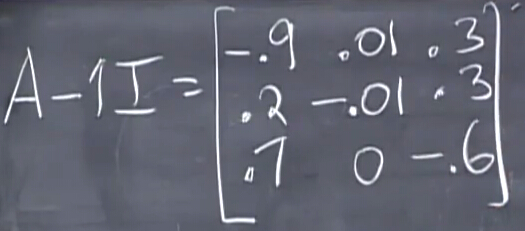
首先，很容易观察出，对于马尔科夫矩阵$A$，其减去单位矩阵$A-I$的所有行的和为0，这说明了什么？说明$A-I$的row vector线性相关，$A-I$为奇异矩阵，那么[1,1,1]在$A^T$的null space中，我们想要的特征向量在$A$的null space中。
这里老师引入一个性质：
$A$的特征值等于$A^T$的特征值，理由是
$det(A-\lambda I = 0)$
⇒det((A−λI)T=