本系列笔记为方便日后自己查阅而写,更多的是个人见解,也算一种学习的复习与总结,望善始善终吧~
马尔科夫矩阵Markov Matrix
马尔科夫矩阵Markov Matrix有两个性质:所有元素大于等于0,所有矩阵的列相加等于1。
这里性质导致一些有趣的特性:
- 马尔科夫矩阵Markov Matrix 的幂依然是马尔科夫矩阵Markov Matrix
- 马尔科夫矩阵Markov Matrix的其中一个特征值为1,其他所有的特征值的绝对值小于1
这二个特性导致了什么呢?看看我们之前关于矩阵的幂的公式:
不难发现随着k的增大,特征值的绝对值小于1的项最终都趋近于0,steady state取决于特征值为1的那一项。那么特征向量呢?
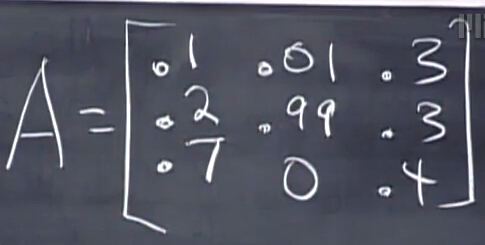
一个例子:
既然我们说其必定存在特征值为1,那么观察:
首先,很容易观察出,对于马尔科夫矩阵A,其减去单位矩阵A−I的所有行的和为0,这说明了什么?说明A−I的row vector线性相关,A−I为奇异矩阵,那么[1,1,1]在AT的null space中,我们想要的特征向量在A的null space中。
这里老师引入一个性质:
A的特征值等于AT的特征值,理由是
det(A−λI=0)
⇒det((A−λI)T=0)
⇒det(AT−λI=0)
求解A的零空间的一个向量很简单,等于求解
很容易求解特征向量,第一行取.6,第三行取.7,第二行求解即可。
马尔科夫矩阵的应用
举例子:
初始状态为[0, 1000]
U是两个城市的人口,矩阵A代表的两个城市之间人口的转化(即从城市cal到mass或反之的人数比例),明显最终的稳态取决于矩阵A,由于这里假设总人口不变,所以矩阵A是马尔科夫矩阵,于是利用上一课的内容求解通式:
得到结果后,我们可以轻松获得任意时刻的状态和稳态。
傅里叶级数
由标准正交基组成的投影矩阵
对于任意向量v都可以由标准正交基q1,q2...qn线性表示:
v=x1q1+x2q2+...+xnqn
我们想要得到x1,由于这里q1,q2...qn彼此正交,我们想到做内积inner prodect可以消去其他项:
qT1v=x1qT1q1+x2qT1q2+...+xnqT1qn
⇒qT1v=x1qT1q1+0+...+0
写为如下形式:
那么x=Q−1v=QTv
⇒xn=qTnv
傅里叶级数
我们知道某个方程:
这个方程和上面的很像,这里每一项也是正交,区别在于这里的qn为函数而非向量。
首先是何为函数的正交?正交意味着内积为0,向量的内积我们知道如何额计算:
那么两个函数之间呢?函数是一堆连续的点,很自然的想到了积分:
对于傅里叶级数,由于存在周期,所以积分从0到2π
于是可以验证傅里叶级数中每一项正交,现在,要怎么求a1,和之前一样,我们让等式两边对cos(x)做内积:
(cos(x))2的积分为π于是a1=1π∫2π0f(x)cos(x)dx
PS:另一位仁兄的笔记
http://blog.csdn.net/suqier1314520/article/details/14056485







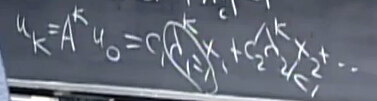
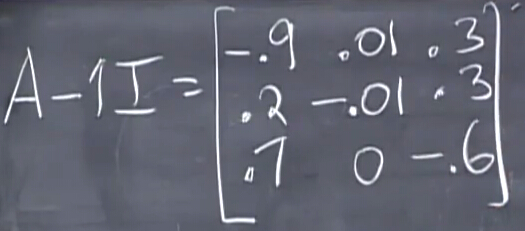
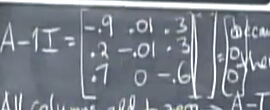

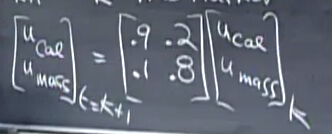
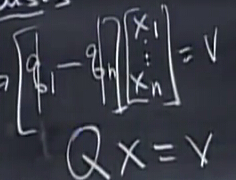

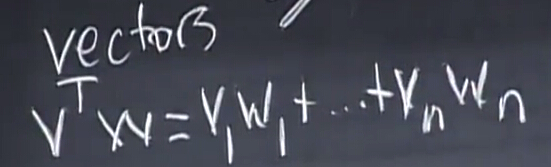
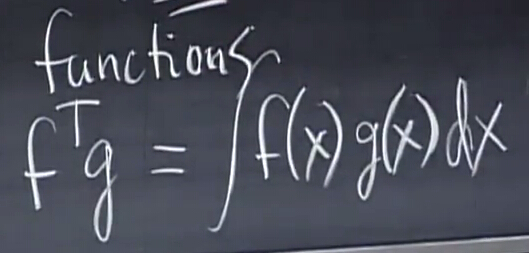















 1795
1795

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








