直观理解KKT条件

最新推荐文章于 2025-03-14 23:51:54 发布

Jie Qiao

最新推荐文章于 2025-03-14 23:51:54 发布

阅读量2.6k

点赞数 14

分类专栏：人工智能文章标签：人工智能

本文链接：https://blog.csdn.net/a358463121/article/details/110249824

版权

人工智能专栏收录该内容

51 篇文章

订阅专栏

直观理解KKT条件

等高线

从等高线讲起。如果我们要优化 $f(x,y)=x^2y$ 这个函数，给定约束为， $x^2+y^2=1$ ，我们希望在满足约束的情况下使得f最大。也就是说，我们希望找到一个最“上方”的平面z，并且该平面要在可行域范围内。这个优化函数的可视化为：
在这里插入图片描述

为了更好的演示，我们一般使用等高线，等高线就是考虑俯视图：

在这里插入图片描述

显然，随着z越来越大，他离我们的圆越来越远，而如果我们缩小z，我们就能找到一个点，恰好与圆相切，这个值就是最优值：

在这里插入图片描述

梯度总是垂直于等高线

现在我们考虑目标函数 $f (x, y) = x y$ ，其梯度为 $<\partial f/\partial x,\partial f/\partial y>=<y,x>$ 。举个例子，我们选择一个点，比如 $x = 2, y = 1$ ，此时梯度为 $< 1, 2 >$ ，将这个向量画在图上，就得到下图白色的直线：

在这里插入图片描述

我们发现梯度总是垂直于等高线的，为什么？首先梯度的直观理解应该是，在这个平面上增长最快的方向，那如果我们考虑两个很相近的平面， $z = 2, z = 2.1$ :

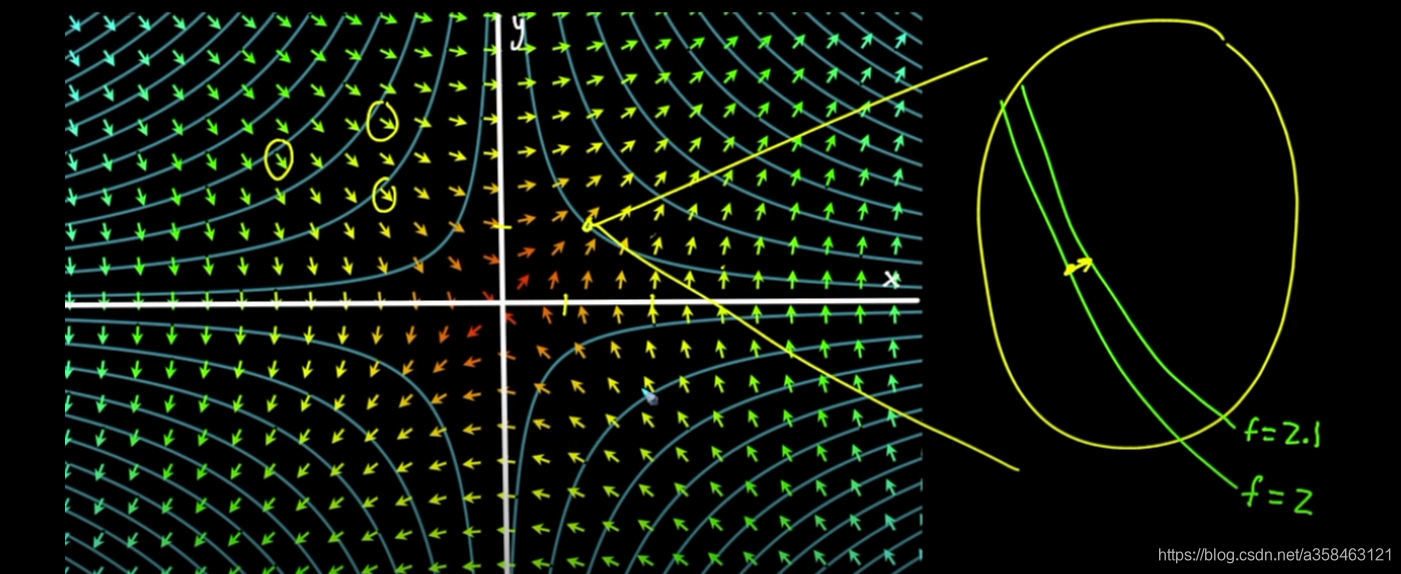
在这里插入图片描述

那么因为两个平面相隔足够小，所以它们的登高线应该几乎是是平行的，于是，这个登高线增长最快的方向，显然就是往与它垂直的方向走（从2走到2.1的方向）。

KKT条件

对于优化问题
$max_{x}f(x) \\s.t.h_j(x)=0,j=1,\dots,q \\g_i(x)\leq 0,i=1,\dots,p$
其KKT条件（必要条件）为，若 $x^*$ 是最优解则一定满足一下条件
$\nabla f(x^*)=\sum_j\lambda_j\nabla h_j(x^*)+\sum_i\mu_i \nabla g_i(x^*) \\\mu_i\geq0,if~g_i(x^*)<0~then~\mu_i=0$
这个条件，可以直接理解为拉格朗日法的推广，就是转换成无约束问题，然后那个无约束的目标函数的梯度等于0.

为了理解这个东西，我们来个简单的例子，
$maxf(x,y)=x^2y \\s.t.x^2+y^2=1$
其中 $h(x,y)=x^2+y^2-1=0$ 。回想一下，我们之前提到，等高线与约束相切的时候是可以得到最优值的。那么这个相切怎么定义呢？实际上，利用梯度总是垂直于登高线的性质，两条线相切，那么在相切点上， $f$ 的梯度，以及约束 $h$ 的梯度，应该是平行的！这意味着：
$\nabla f(x^*)=\lambda\nabla h(x^*)$
这不就是KKT条件嘛！这个垂直的状态就如下图所示：

在这里插入图片描述

那个g的梯度其实就是那个约束的梯度，对于事实上，对于约束我们也可以画出类似的等高线图：

在这里插入图片描述

最后我们来算一下，这个平行的梯度在哪个位置：
$\begin{array}{l} f( x,y) =x^{2} y\\ h( x,y) =x^{2} +y^{2} -1\\ x^{2} +y^{2} =1\\ \nabla f=< 2xy,x^{2} >\\ \nabla h=< 2x,2y > \end{array}$
我们希望找到成比例的梯度：
$\begin{aligned} & \nabla f=\lambda \nabla h\\ \Longrightarrow & \begin{cases} 2xy=2\lambda x\\ x^{2} =2\lambda y \end{cases} \end{aligned}$
联合等式：
$\begin{array}{l} 2xy=2\lambda x\\ x^{2} =2\lambda y\\ x^{2} +y^{2} =1 \end{array}$

我们可以求出 $\displaystyle y^{2} =\frac{1}{3} ,x^{2} =\frac{2}{3}$ ，将这个值带到目标函数里， $\displaystyle x^{2} y=\frac{2}{3}\sqrt{\frac{1}{3}} =\frac{2\sqrt{3}}{9}$ ，这个就是目标函数的最优解啦！到这里我们只考虑了等式约束，也就是 $h = 0$ 的情况，没有考虑 $g_j(x)\le0$ 的情况，其实，到这里已经很好理解了，如果最优值的点是落在 $g_j(x)<0$ 处的话，那么我们是没有必要让这个 $g_j$ 的梯度也跟 $f$ 的梯度垂直，因为落在里面的时候在各个方向都可以任意的移动，并不会受到约束，所以我们如果 $g_j(x)<0$ ，那么我们令其对应的 $\mu_j=0$ 。