【CFD理论】雷诺时均模型（RANS）

目录

时均化概念

时均N-S方程推导

连续性方程

动量方程

方程封闭

RSM

Boussinesq假设

时均化概念

雷诺平均纳维-斯托克斯方程（RANS 方程）是流体流动的运动时间平均方程。方程背后的思想是雷诺分解，即将瞬时量分解为其时间平均量和波动量。

将速度矢量分解如下：

同样的，对于压力和其他标量，也可进行时均化处理：

对于时均量，有以下计算规则：

首先写一些符合认知的

• 扰动的时均量为0

• 时均量为一个常数

• 对常数乘时变量的总时均量，可以分开写

然后可得

最后再推导一个重要的，后续会用

将AB的时均量展开，得到以下公式

然后分项化简

最后结果如下：

时均N-S方程推导

假设为不可压缩流体，此时得到N-S方程如下：

此处为爱因斯坦求和约定表示的格式

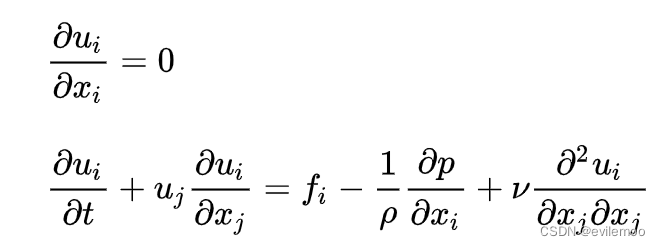
连续性方程

动量方程

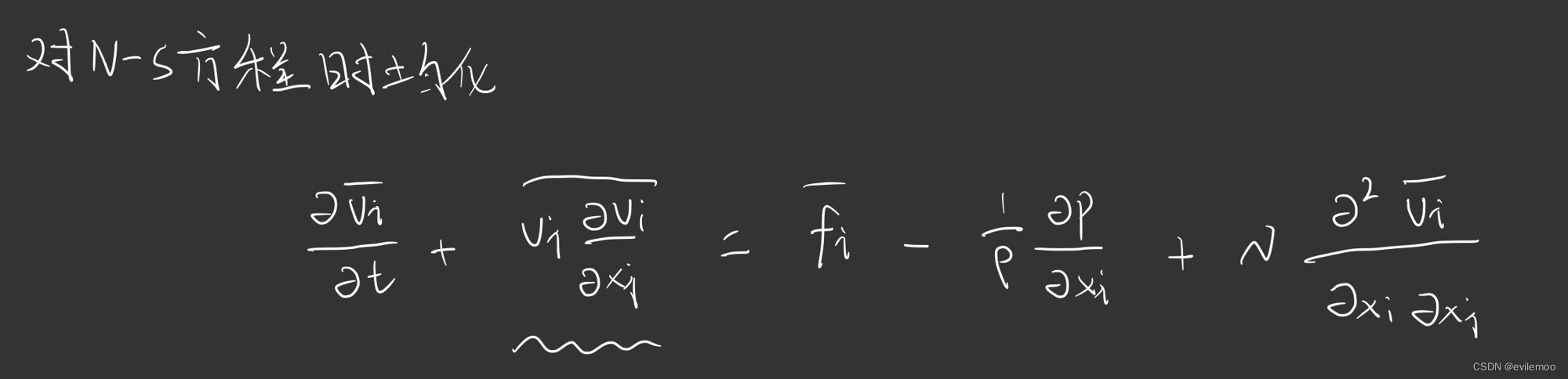
对第二项，根据上述时均计算规则展开得到

对上式的第二项继续计算如下：

最终得到N-S方程的雷诺时均方程如下：

此外，如果考虑密度，可以得到方程如下：

方程封闭

正常的N-S方程包含三个方向的动量守恒方程和一个连续性方程，正好要求解三个方向的速度与压力，方程是闭合的。然而由于高度非线性，没有什么好的办法求解N-S方程。

在对N-S方程时均化，得到RANS方程后，需要求解的变量又多了一个，即雷诺应力。

RSM

雷诺应力模型是求解雷诺应力张量中每个项的输运方程。加上一个额外的尺度确定方程。这意味着在二维流中需要五个额外的输运方程，而在三维流中必须求解七个额外的输运方程。

Boussinesq假设

Boussinesq 假设用于 Spalart-Allmaras 模型和二方程模型。这种方法的优点是与湍流粘度的计算相关的计算成本相对较低。Boussinesq 假设的缺点，它假设是一个各向同性的标量，在有些情景中并不适用。