支持向量机（SVM）关键点攻略（最大间隔，对偶问题）

　　近来学习支持向量机，杂七杂八的视频、文章看了一大堆，总算是对SVM中比较难以理解的部分有了一些心得体会，因而记录在此。一方面方便自己以后复习，另一方面也是分享给有需要的朋友查看，另外有理解错误的地方希望大家能够指出，多多讨论，共同进步。

---

1. SVM提出背景

1) 哪条线最好？

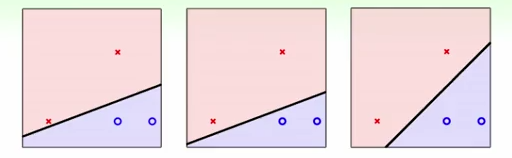
　　容易看出，第三幅图里的分割超平面看起来“更好”。
　　
2) 为什么好？

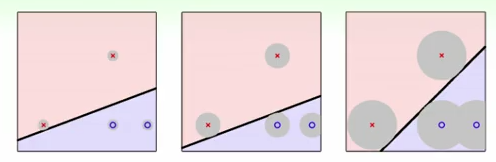
　　能够容忍更多噪声—>所有样本与分割超平面的距离尽可能远—>最差的样本（离分割超平面最近的样本）与分割超平面的距离要尽可能远

因此，SVM的目的就是从无数多个分割超平面中，找到这样最好的分割超平面。

2. SVM的优化目标

　　这个部分是我纠结了很久，被各种资料里讲解的几何间隔和函数间隔绕晕了，不知道有没有和我一样的朋友。。。因此我决定绕过函数间隔，只从几何间隔的角度来考虑这个事情，并给出推导过程。
　　接下来先简单谈谈几何间隔的定义。
　　令($x^{(i)}$,$y^{(i)}$)，$i=1,2,...,m$为训练集中的一个样本，一共有$m$个样本。$w^Tx+b=0$为超平面，$w$和$b$是我们要求的参数。则样本($x^{(i)}$,$y^{(i)}$)到超平面$w^Tx+b=0$的距离（几何间隔）定义为：

$$\gamma=\frac{|w^Tx+b|}{||w||}$$
　　因为 $w^Tx+b=0$能正确分类样本，所以有： $$y(w^Tx+b)>0$$
　　因此为了计算方便，可以去掉 $\gamma$表达式中的绝对值，写成： $$\gamma=\frac{y(w^Tx+b)}{||w||}$$
　　事实上，y取±1时，上式与最开始的定义完全等价。
　　 $\color{red}{重点来了！}$
　　上面说到，我们要找的线描述为： 离分割线最近的样本与分割线的距离尽量远
　　什么叫离分割线最近的样本？答：就是所有样本与分割线的距离，都大于等于该样本与分割线的距离。假设该样本为 $(x^{(k)},y^{(k)})$，则有： $$\frac{y^{(i)}(w^Tx^{(i)}+b)}{||w||}\ge\frac{y^{(k)}(w^Tx^{(k)}+b)}{||w||},i=1,2,...,m$$
　　此为 约束条件。
　　什么是尽量远？答： $$max_{w,b} \frac{y^{(k)}(w^Tx^{(k)}+b)}{||w||}$$
　　此为 目标。
　　为了书写方便，不妨设 $y^{(k)}(w^Tx^{(k)}+b)=K$（样本已确定，是一个常数），并约去约束条件中的分母，则上述两式联合起来可写为： $$max_{w,b} \frac{K}{||w||}$$

s.t.