支持向量机,英文为Support Vector Machine,简称SV机(论文中一般简称SVM)。它是一种監督式學習的方法,它广泛的应用于统计分类以及回归分析中。
支持向量机属于一般化线性分类器.他们也可以认为是提克洛夫规范化(Tikhonov Regularization)方法的一个特例.这族分类器的特点是他们能够同时最小化经验误差与最大化几何边缘区.因此支持向量机也被称为最大边缘区分类器。在统计计算中,最大期望(EM)算法是在概率(probabilistic)模型中寻找参数最大似然估计的算法,其中概率模型依赖于无法观测的隐藏变量(Latent Variabl)。最大期望经常用在机器学习和计算机视觉的数据集聚(Data Clustering)领域。最大期望算法经过两个步骤交替进行计算,第一步是计算期望(E),也就是将隐藏变量象能够观测到的一样包含在内从而计算最大似然的期望值;另外一步是最大化(M),也就是最大化在 E 步上找到的最大似然的期望值从而计算参数的最大似然估计。M 步上找到的参数然后用于另外一个 E 步计算,这个过程不断交替进行。
Vapnik等人在多年研究统计学习理论基础上对线性分类器提出了另一种设计最佳准则。其原理也从线性可分说起,然后扩展到线性不可分的情况。甚至扩展到 使用非线性函数中去,这种分类器被称为支持向量机(Support Vector Machine,简称SVM)。支持向量机的提出有很深的理论背景。 支持向量机方法是在近年来提出的一种新方法。
SVM的主要思想可以概括为两点: (1) 它是针对线性可分情况进行分析,对于线性不可分的情况,通过使用非线性映射算法将低维输入空间线性不可分的样本转化为高维特征空间使其线性可分,从而 使得高维特征空间采用线性算法对样本的非线性特征进行线性分析成为可能;(2) 它基于结构风险最小化理论之上在特征空间中建构最优分割超平面,使得学习器得到全局最优化,并且在整个样本空间的期望风险以某个概率满足一定上界。
在学习这种方法时,首先要弄清楚这种方法考虑问题的特点,这就要从线性可分的最简单情况讨论 起,在没有弄懂其原理之前,不要急于学习线性不可分等较复杂的情况,支持向量机在设计时,需要用到条件极值问题的求解,因此需用拉格朗日乘子理论,但对多 数人来说,以前学到的或常用的是约束条件为等式表示的方式,但在此要用到以不等式作为必须满足的条件,此时只要了解拉格朗日理论的有关结论就行。
介绍
支持向量机将向量映射到一个更高维的空间里,在这个空间里建立有一个最大间隔超平面。在分开数据的超平面的两边建有两个互相平行的超平面。分隔超平 面使两个平行超平面的距离最大化。假定平行超平面间的距离或差距越大,分类器的总误差越小。一个极好的指南是C.J.C Burges的《模式识别支持向量机指南》。van der Walt 和 Barnard 将支持向量机和其他分类器进行了比较。
动机
我们通常希望分类的过程是一个机器学习的过程。这些数据点并不需要是 中的点,而可以是任意
中的点,而可以是任意 (统计学符号)中或者
(统计学符号)中或者 (计算机科学符号) 的点。我们希望能够把这些点通过一个n-1维的超平面分开,通常这个被称为线性分类器。有很多分类器都符合这个要求,但是我们还希望找到分类最佳的平面,即使得属于两个不同类的数据点间隔最大的那个面,该面亦称为最大间隔超平面。如果我们能够找到这个面,那么这个分类器就称为最大间隔分类器。
(计算机科学符号) 的点。我们希望能够把这些点通过一个n-1维的超平面分开,通常这个被称为线性分类器。有很多分类器都符合这个要求,但是我们还希望找到分类最佳的平面,即使得属于两个不同类的数据点间隔最大的那个面,该面亦称为最大间隔超平面。如果我们能够找到这个面,那么这个分类器就称为最大间隔分类器。
问题定义
我们考虑以下形式的样本点
其中ci为1或−1 --用以表示数据点属于哪个类.  是一个p − (统计学符号), 或 n − (计算机科学符号) 维向量,其每个元素都被缩放到[0,1]或[-1,1].缩放的目的是防止方差大的随机变量主导分类过程.我们可以把这些数据称为“训练数据”,希望我们的支持向量机能够通过一个超平面正确的把他们分开。超平面的数学形式可以写作
是一个p − (统计学符号), 或 n − (计算机科学符号) 维向量,其每个元素都被缩放到[0,1]或[-1,1].缩放的目的是防止方差大的随机变量主导分类过程.我们可以把这些数据称为“训练数据”,希望我们的支持向量机能够通过一个超平面正确的把他们分开。超平面的数学形式可以写作
根据几何知识,我们知道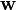 向量垂直于分类超平面。加入位移b的目的是增加间隔.如果没有b的话,那超平面将不得不通过原点,限制了这个方法的灵活性。
向量垂直于分类超平面。加入位移b的目的是增加间隔.如果没有b的话,那超平面将不得不通过原点,限制了这个方法的灵活性。
由于我们要求最大间隔,因此我们需要知道支持向量以及(与最佳超平面)平行的并且离支持向量最近的超平面。我们可以看到这些平行超平面可以由方程族:
来表示。
如果这些训练数据是线性可分的,那就可以找到这样两个超平面,在它们之间没有任何样本点并且这两个超平面之间的距离也最大.通过几何不难得到这两个超平面之间的距离是 2/|w|,因此我们需要最小化 |w|。同时为了使得样本数据点都在超平面的间隔区以外,我们需要保证对于所有的 i 满足其中的一个条件
这两个式子可以写作:
原型
现在寻找最佳超平面这个问题就变成了在(1)这个约束条件下最小化|w|.这是一个二次規劃QP(quadratic programming)最优化中的问题。
更清楚的,它可以表示如下:
-
最小化
 , 满足
, 满足
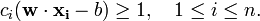 。
。
1/2 这个因子是为了数学上表达的方便加上的。
对偶型(Dual Form)
把原型的分类规则写作对偶型,可以看到分类器其实是一个关于支持向量(即那些在间隔区边缘的训练样本点)的函数。
支持向量机的对偶型如下: 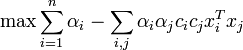 并满足αi > = 0
并满足αi > = 0
软间隔
1995年, Corinna Cortes 与Vapnik 提出了一种改进的最大间隔区方法,这种方法可以处理标记错误的样本。如果可区分正负例的超平面不存在,则“软边界”将选择一个超平面尽可能清晰地区分样 本,同时使其与分界最清晰的样本的距离最大化。这一成果使术语“支持向量机”(或“SVM”)得到推广。这种方法引入了松驰参数ξi以衡量对数据xi的误分类度。
-
 。
。
随后,将目标函数与一个针对非0ξi的惩罚函数相加,在增大间距和缩小错误惩罚两大目标之间进行权衡优化。如果惩罚函数是一个线性函数,则等式(3)变形为










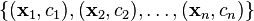

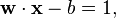

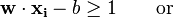
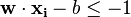

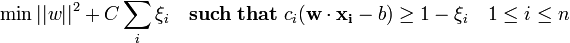














 8593
8593

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








