支持向量机（Support Vector Machines）

乔大将军

于 2023-12-26 17:47:46 发布

阅读量1.1k

点赞数 19

分类专栏：机器学习文章标签：支持向量机 leetcode 算法

本文链接：https://blog.csdn.net/JamesSwifte/article/details/134926392

版权

机器学习专栏收录该内容

24 篇文章 3 订阅

订阅专栏

一、目的：

理解支持向量机（Support Vector Machines）的一些基础理论知识，如支持向量（Support Vector）、分隔超平面（Separating hyperplane）等重要概念的求解流程，进而掌握SMO高效优化算法的优化思想，以此对现有的数据进行优化，提升分类效果。

二、实验内容

1. 基于SVM的iris数据集识别

（1）构建SVM程序，实现对iris数据集的分类。

（2）要求分别使用线性SVM和核化SVM方法实现。并对比分析两种方法的区别。

2. 基于SVM的pima-indians-diabetes（pima印地安纳糖尿病）数据集识别

（1）构建SVM程序，实现对pima-indians-diabetes数据集的分类。

三、支持向量机本质是解决分类问题

例如在二维平面区分两类样本需要找到一条直线，这条直线就称为一维决策平面

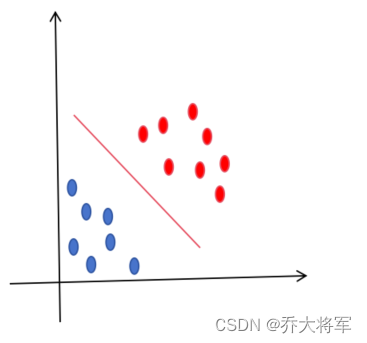
在三维就需要找到一个二维平面来分类两种类型样本，称为二维决策平面

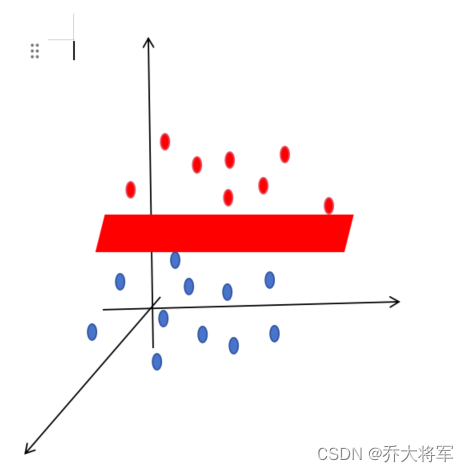
延伸到 n样本 * m维度,用一个m-1维的超平面来分类 $w_{1}x_{1}+w_{2}x_{2}+...+w_{m}x_{m}+B=0$ w为权值

$\begin{pmatrix} x_{11}, x_{12}, ... ,x_{1m}& & \\ x_{21},x_{22},...,x_{2m}& & \\ ...,...,...,...& & \\ x_{n1},x_{n2},...,x_{nm}& & \end{pmatrix}$

此时样本1，2两点决定间隔大小，因此称为支持向量

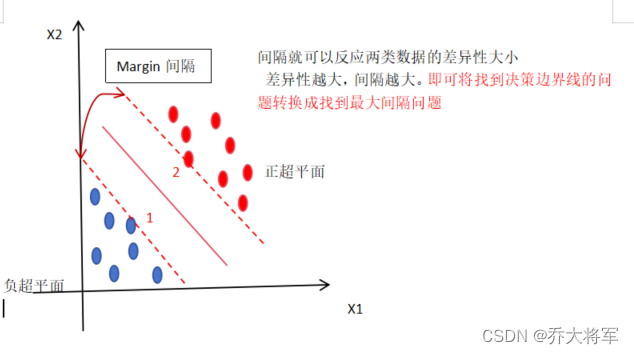
得出正超平面，决策平面，负超平面的公式为:

$w_{1}x_{1}+w_{2}x_{2}=1\\ w_{1}x_{1}+w_{2}x_{2}=0\\ w_{1}x_{1}+w_{2}x_{2}=-1$

若存在一个异常样本3如

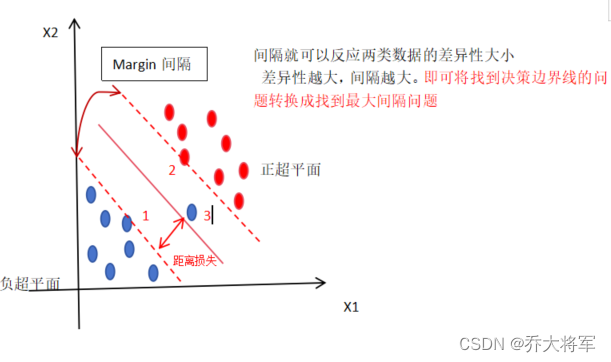
考虑到损失距离的一个最优化求解的这样一个间隔叫做软间隔（有容错率），而直接以样本3为负超平面间隔叫硬间隔。

升维转换和核技巧：面对低维无法产生超平面来区分两类数据时，可以采用升维的方法。如

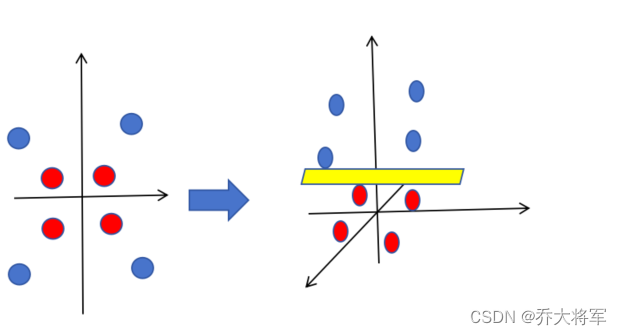
即： $\begin{pmatrix} x_{11} ,x_{12} & \\ x_{21} , x_{22}& \\ ...,...&\\ x_{n1},x_{n2} \end{pmatrix}\Rightarrow \begin{pmatrix} x_{11},x_{12},...,x_{1m} & & \\ x_{21},x_{22},...,x_{2m} & & \\ ....,...,...& & \\ x_{n1},x_{n2},...,x_{nm} \end{pmatrix}$

需要找到一个复杂的升维函数，这往往是费时费力的，引入kernel Trick(核技巧)，直接获得高维度的向量差异度。

四、如何求解SVM的决策超平面？

前面说过目标是：最大化（maximize）正负超平面间的间隔距离L。

例如：二维平面

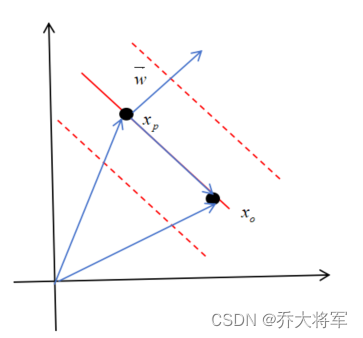
取 $x_{o}$ , $x_{p}$ 点位于决策超平面上，那么有公式

$\left\{\begin{matrix} w_{1}x_{1o}+w_{2}x_{2o}+b=0\\ w_{1}x_{1p}+w_{2}x_{2p}+b=0\\ w_{1}(x_{1o}-x_{1p})+w_{2}(x_{2o}-x_{2p})+b=0\\ \end{matrix}\right.$

表示向量 $\vec{w}$ 与向量 $\vec{x_{o}}-\vec{x_{p}}$ 的点积结果为0，即 $\vec{w}\times (\vec{x_{o}}-\vec{x_{p}})=0$ ,可知向量 $\vec{w}$ 垂直于决策超平面。

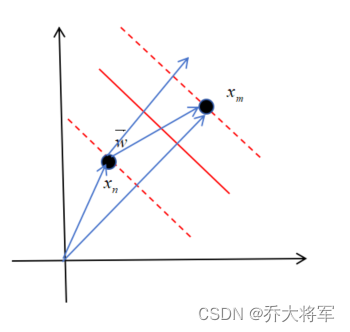
在正负超平面上取两点两点 $x_{n},x_{m}$ ,这两点都支持向量，那么有公式：

$\left\{\begin{matrix} w_{1}x_{1m}+w_{2}x_{2m}+b=1\\ w_{1}x_{1n}+w_{2}x_{2n}+b=-1\\ w_{1}(x_{1m}-x_{1n})+w_{2}(x_{2m}-x_{2n})+b=2\\ \end{matrix}\right.$

表示向量 $\vec{w}$ 与向量 $\vec{x_{m}}-\vec{x_{n}}$ 的点积结果为2，即 $\vec{w}\times (\vec{x_{m}}-\vec{x_{n}})=2$

进一步得知： $\parallel \vec{w}\parallel\bullet cos\theta \bullet \parallel \vec{x_{m}}-\vec{x_{n}}\parallel = 2$

而 $L$ (间隔距离)是向量 $\vec{x_{m}}-\vec{x_{n}}$ 在向量 $\vec{w}$ 上的投影，即 $L=cos\theta \bullet \parallel \vec{x_{m}}-\vec{x_{n}}\parallel$

得 $L\bullet \parallel \vec{w}\parallel =2\Rightarrow L=\frac{2}{\parallel \vec{w}\parallel }$

要使得 $L$ (间隔距离)最大化问题转换为即求在约束条件下的 $\parallel \vec{w}\parallel$ 最小化问题。

约束表达式均为仿射函数约束，如上图所示。约束表达式可以进一步提炼为

$y_{i}*(\vec{w} \bullet\vec{x_{i}} +b)\geqslant 1$ ,and $\parallel \vec{w}\parallel = \sqrt{w_{1}^{2} +w_{2}^2}$

subject to $y_{i}*(\vec{w} \bullet\vec{x_{i}} +b)\geqslant 1$ , $i=1,2,3,4......$

to minimize $\parallel\vec{w} \parallel$ , get function $f(w)=\frac{\parallel \vec{w}\parallel^2 }{2}$ 消除根号的影响，故平方

subject to $g_{i}(w,b) = y_{i}*(\vec{w} \bullet\vec{x_{i}} +b)-1\geqslant 0,i=1,2,3,4.....$

求多元函数的条件极值，即函数 $f(w)=\frac{\parallel \vec{w}\parallel^2 }{2}$ ，在条件 $g_{i}(w,b) = y_{i}*(\vec{w} \bullet\vec{x_{i}} +b)-1\geqslant 0,i=1,2,3,4.....$ 下求极值，必须要在条件为等式的情况下，即可转换为 $g_{i}(w,b) = y_{i}*(\vec{w} \bullet\vec{x_{i}} +b)-1= p_{i}^2,i=1,2,3,4.....$

引入拉格朗日乘子，得到公式 $L(w,b,\lambda _{i},p_{i}) =\frac{\parallel \vec{w}^2\parallel }{2} -\sum_{s}^{i}\lambda _{i}\ast (y_{i}*(\vec{w} \bullet\vec{x_{i}} +b)-1-p_{i}^2),i=1,2,3,4.....s$

求极值：求偏导 $\frac{\partial L}{\partial w}=0,\frac{\partial L}{\partial b}=0,\frac{\partial L}{\partial \lambda _{i}}=0,\frac{\partial L}{\partial p_{i}}=0$ ，

得到 $\vec{w}\bullet \sum_{i=1}^{s}\lambda _{i}y_{i}\vec{x_{i}}=0$

$-\sum_{i=1}^{s}\lambda _{i}y_{i}=0$ ,

$y_{i}\ast (\vec{w}\bullet \vec{x_{i}}+b)-1-p_{i}^2=0$ ,

$\lambda _{i}p_{i}^2=0$ ，

$\lambda _{i}\geqslant 0$ (把 $\lambda _{i}$ 当作违背约束条件的惩罚系数，IF $\lambda _{i}< 0$ ,不满足约束条件)

SVM的对偶性

假设最优解为 $w^*$ , $b^*$

构造新方程：

$q(\lambda _{i})=minimize(L(w,b,\lambda _{i}))=minimize(f(w)-\sum_{i=1}^{s}\lambda _{i}g_{i}(w,b)),i=1,2,3,4....s$

因为 $\lambda _{i}\geqslant 0$ ， $g_{i}(w,b)\geq 0$

所以 $q(\lambda _{i})\leqslant q(\lambda _{i}^*)\leqslant f(\vec{w}^*)\leqslant f(w)$

弱对偶： $q(\lambda _{i})<f(\vec{w}^*)$ ,强对偶： $q(\lambda _{i})=f(\vec{w}^*)$

根据多偶性将求最小问题转换为求最大问题。

$q(\lambda _{i}^*)=maximize(q(\lambda _{i}))$

最后变换得到：

$maximize\, q(\lambda _{i})=maximize(\sum_{i=1}^{s}\lambda _{i}-\frac{1}{2}\sum_{s}^{i=1}\sum_{s}^{j=1}\lambda _{i}\lambda _{j}y_{i}y_{j}\vec{x_{i}}\vec{x_{j}}) \; subject \, to\, \lambda _{i}\geqslant 0,i=1,2,3,4....s$

求解 $\lambda _{i}$ ,再根据 $\vec{w}=\sum_{i=1}^{s}\lambda _{i}y_{i}\vec{x_{i}}$ 求解 $\vec{w}$

再根据 $y_i*(\vec{w}\bullet \vec{x_i}+b)-1=0$ 求解b。

五、核技巧

然而对于

存在无解的情况

方法1：升维原维度向量 $\vec{x}$ --->新维度向量 $T(\vec{x})$ ,这种方法需要找到一个合适的唯独转换函数 $T$ 耗费的资源较多。

方法2：通过核函数 $k(\vec{x_{i}},\vec{x_{j}})$ 直接获得高维度的向量差异度。

常用的核函数：高斯核函数(RBF)Radial Basis Kernel

$K(\vec{x_i},\vec{x_j})=e^{-r\parallel \vec{x_i}-\vec{x_j}\parallel }$ 其直接反映了两个向量的相似度大小。

六、软间隔

以上说的都是硬间隔的决策超平面的求解方法，当出现异常点时防止过拟合引入软间隔。

原间隔的约束条件： $y_i*(\vec{w}\bullet \vec{x_{i}}+b)\geqslant 1$

点 $\partial$ 违背约束条件： $y_{\partial }*(\vec{w}\bullet \vec{x_\partial }+b)<1$

量化点 $\partial$ 误差： $\varepsilon _{\partial }=1-y_\alpha *(\vec{w}\bullet \vec{x_\partial }+b)$

对于任意一点 $\varepsilon _{i}$ ,有 $\varepsilon _{i }=max(0,1-y_i *(\vec{w}\bullet \vec{x_i }+b))$ (铰链损失函数)

得到 $minimize\, f(w)=\frac{\parallel \vec{w}\parallel^2 }{2}+C*\sum_{i=1}^{s}\varepsilon _i$ ， $C$ 为超参数。

当 $C$ 越大，表明容忍度越小，当 $C$ 趋于无穷时，为硬间隔。

七、实验代码

import pandas as pd  # 数据科学计算工具
import numpy as np  # 数值计算工具
import matplotlib.pyplot as plt  # 可视化
import seaborn as sns  # matplotlib的高级API
pima = pd.read_csv('C:\Analysis\data\download-self\PimaIndiansdiabetes.csv')
pima.head()
#pima.head()默认前5行，pima.tail()默认最后5行，查看Series或者DataFrame对象的小样本，当然我们也可以传递一个自定义数字
pima.shape,pima.keys(),type(pima)
pima.describe()
# panda的describe描述属性，展示了每一个字段的
#【count条目统计，mean平均值，std标准值，min最小值，25%，50%中位数，75%，max最大值】
pima.groupby('Outcome').size()
#按照是否发病分组，并展示每组的大小
pima.hist(figsize=(16, 14));
#查看每个字段的数据分布；figsize的参数显示的是每个子图的长和宽
sns.pairplot(pima, vars=pima.columns,hue = 'Outcome')
sns.pairplot(pima, vars=pima.columns[:-1], hue='Outcome')
plt.show()
# sns.pairplot(pima,diag_kind='hist', hue='Outcome')
sns.pairplot(pima, diag_kind='hist');
pima.plot(kind='box', subplots=True, layout=(3,3), sharex=False,sharey=False, figsize=(16,14));

# 箱线图（Boxplot）也称箱须图（Box-whisker Plot），是利用数据中的五个统计量：最小值、第一四分位数、中位数、第三四分位数与最大值
pima.plot(kind='box', subplots=True, layout=(3,3), sharex=False,sharey=False, figsize=(16,14))
c = pima.iloc[:,0:8].corr()# 选择特征列，去掉目标列
plt.subplots(figsize=(14,12)) # 可以先试用plt设置画布的大小，然后在作图，修改
sns.heatmap(corr, annot = True) # 使用热度图可视化这个相关系数矩阵
# 导入和特征选择相关的包
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
X = pima.iloc[:, 0:8]  # 特征列 0-7列，不含第8列
Y = pima.iloc[:, 8]  # 目标列为第8列

select_top_4 = SelectKBest(score_func=chi2, k=4)  # 通过卡方检验选择4个得分最高的特征
fit = select_top_4.fit(X, Y)  # 获取特征信息和目标值信息
features = fit.transform(X)  # 特征转换
#features[0:5]
#新特征列的前5行
# 因此，表现最佳的特征是：Glucose-葡萄糖、Insulin-胰岛素、BMI指数、Age-年龄
# 构造新特征DataFrame
X_features = pd.DataFrame(data = features, columns=['Glucose','Insulin','BMI','Age']) 
#标准化
# 它将属性值更改为 均值为0，标准差为1 的 高斯分布.
# 当算法期望输入特征处于高斯分布时，它非常有用
from sklearn.preprocessing import StandardScaler
rescaledX = StandardScaler().fit_transform(
    X_features)  # 通过sklearn的preprocessing数据预处理中StandardScaler特征缩放 标准化特征信息
X = pd.DataFrame(data=rescaledX, columns=X_features.columns)  # 构建新特征DataFrame
# 切分数据集为：特征训练集、特征测试集、目标训练集、目标测试集
X_train, X_test, Y_train, Y_test = train_test_split(
    X, Y, random_state=2019, test_size=0.2)
#SVM模型
from sklearn.svm import SVC
from sklearn.metrics import classification_report, confusion_matrix

classifier = SVC(kernel = 'rbf')
classifier.fit(X_train_pca, Y_train)
# 使用SVC预测生存

y_pred = classifier.predict(X_test_pca)
cm = confusion_matrix(Y_test, y_pred)
print(cm)#预测真确和错误的个数
print(classification_report(Y_test, y_pred))

乔大将军

关注

19
点赞
踩
22

收藏

觉得还不错? 一键收藏
0
评论
支持向量机（Support Vector Machines）

理解支持向量机（Support Vector Machines）的一些基础理论知识，如支持向量（Support Vector）、分隔超平面（Separating hyperplane）等重要概念的求解流程，进而掌握SMO高效优化算法的优化思想，以此对现有的数据进行优化，提升分类效果。需要找到一个复杂的升维函数，这往往是费时费力的，引入kernel Trick(核技巧)，直接获得高维度的向量差异度。以上说的都是硬间隔的决策超平面的求解方法，当出现异常点时防止过拟合引入软间隔。
复制链接

扫一扫