曲线拟合,俗称拉曲线,是一种把现有数据透过数学方法来代入一条数式的表示方式。科学和工程问题可以通过诸如采样、实验等方法获得若干离散的数据,根据这些数据,我们往往希望得到一个连续的函数(也就是曲线)或者更加密集的离散方程与已知数据相吻合,这过程就叫做拟合。
本条目讲述如何透过拉曲线的方法来进行插值法运算及递归分析的基础。
[编辑]将点结成直线或多项式曲线
首先看一看一个一次多项式例子
在笛卡儿平面上,这是一条直线,而这条直线的斜率是a,(从比较斜率-交点式y = mx + b 中知道 a 等同于 m)。而我们知道任何两点都有一条直线穿过,因此一次多项式可以串起任何两个点。
如果多次式的次数增加为2
这条多项式就串起任何3点。
如果多次式的次数再增加为3
这条多项式就串起任何4点。
对于这条多项式,更正确的描述是这条多项式附合任何4个限制。限制可以是一点(x,y)、角度或曲率(即半径的反数 1/R)。角度和曲率的限制通常在曲线的终端,因此称为终端条件 。为了样条(spline) 的交接平滑,通常会用到全等的终端条件。 也可以增加如曲率变化等高阶约束。例如,在高速公路立体交叉点cloverleaf的设计中,可以用来理解当汽车绕着交叉点运动时作用在汽车上的力,并依此设定合理的限定时速。
一次多项式也可以拟合一个单点和一个角度,三次多项式则可以拟合两点,一个角度约束以及一个曲率约束。许多其它类型的约束组合也同样可以用低阶或者高阶多项式来拟合。
如果有超过n+1个约束(n是多项式的阶次),我们仍然可以使用多项式拟合。通常一个满足所有约束的精确拟合不一定能够得到(但是有可能得到,例如,用一次多项式拟合共线的三点三点共线)。通常,我们需要使用一些方法来评价拟合的好坏。最小二乘法就是用来评价差别的一种常用的方法。
为什么不能通过提高多项式的次数来更好的拟合曲线呢?关于这点,有以下原因:
- 即使存在精确的拟合,也不意味着必须得到这样的拟合。根据使用的算法不同,我们可能遇到分歧,要么精确的拟合无法得到,要么需要太多的计算机时去得到精确的拟合。不管哪种情况,最终都会以得到近似拟合而结束。
- 我们往往宁愿得到一个近似的拟合,而不愿为了精确拟合数据而使拟合的曲线产生扭曲。
- 高次多项式往往有高度波动的特性。如果我们通过两点"A"和“B”作一条曲线,我们希望这条曲线也能通过"A"和“B”的中点。但是对于高次多项式,情况就不是这样了,高次多项式曲线往往可能有很大或者很小的幅值。对于低次多项式,曲线将没有很大波动,而能通过中点(对于一次多项式,甚至能保证肯定通过中点)。
[编辑]参考文献
- YAN Kun. Research on adaptive connection equation in discontinuous area of data curve. DOI:10.3969/j.issn.1004-2903.2011.01.018








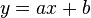
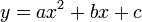
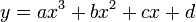














 458
458

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








