机器学习---牛顿方法

1.一维情景

• 给定一条曲线
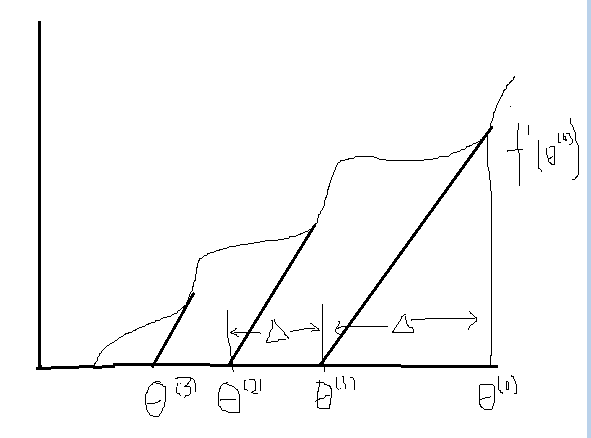
• 目的：寻找当θ为何值时,f(θ)=0

• 公式推导如下：
• $f'(θ)={f(θ^{(0)})\over△}$
• $△={f(θ^{(0)})\over{f'(0)}}$
• $θ^{(1)}=θ^{(0)}-{f(θ^{(0)})\over{f'(0)}}$
• 所以推导到t的情况，一般公式为：
• $θ^{(t+1)}=θ^{(t)}-{f(θ^{(t)})\over{f'(t)}}$
• 此上推导为牛顿的一次迭代
• 牛顿方法是一个收敛速度比较快的算法

---

2.二维情景

• $θ^{(t+1)}=θ^{(t)}-H^{-1}▽_el$
• H为Hessian为一个n*n的矩阵
• 缺点为每次迭代都需要求取一个Hessian矩阵的逆，对于一些特征量合理的算法而言，是一个比较快的算法;但是一旦特征值较多,每一次求逆都需要大量的计算

---

16:00‘提到的问题

3.广义线性模型(GLM)

1.指数分布族

• P（y|x;θ）
• ① y∈R 并且满足高斯分布（Gaussian distribution ）得到了基于最小二乘法的线性回归
• ②y∈{0,1} 0-1分布，即是伯努利分布（Bernoulli ） 得到了logistic回归

---

• sigmoid函数是一个可以引出logistic回归的最为自然的默认选择
• P（y=1;φ）=φ
• 高斯分布$N（μ，σ^2）$
• 以上两种分布都是一类分布的特例，叫做指数分布族
• $P(y,η)=b(y)exp(η^TT(y)-a(η))$
• 说明：
• η—自然参数（natural parameter）
• T(y)—充分统计量（sufficient statistic）
• a,b.T的形式，当选取不同的η，会得到不同的概率，选取特定的a,b,T会得到上述的两种模型

---

2.伯努利分布

• Ber(φ)

• P(y=1;φ) = φ

  P(y;φ)
  =$φ^y(1-φ)^{1-y}$
  =$exp(logφ^y(1-φ)^{1-y})$
  =$exp(ylogφ+(1-y)log(1-φ))$
  =$exp(ylog{φ\over{1-φ}}+log(1-φ))$

---

• $η=log{φ\over{1-φ}}$①
• 将公式颠倒过来得到
• $φ={1\over{1+e^{-η}}}$②
• 通过了公式①奇迹的得到了logistic函数

---

$a(η)=-log(1-φ)=log(1+e^η)$

$T(y)=y$

$b(y)=1$

以上得到了a,b,T,指数分布族特殊化情景

3.高斯分布

• $N（μ，σ^2）$
• 设定$σ^2=1$
  

  ${1\over{\sqrt{2π}}}exp(-{1\over2}(y-μ)^2)$
  =${1\over{\sqrt{2π}}}exp(-{{1\over2})y^2}exp(μy+{1\over2}μ^2))$

---

经过以上推导得到了a,b,T

$b(y)={1\over{\sqrt{2π}}}exp(-{{1\over2})y^2}$
$T(y)=y$
$a(η)=-{1\over2}μ^2$

---

4.其它

• ⑴泊松分布（Poisson distribution）
• 计数建模—放射性衰变的数目，网站的访客数量，商店的顾客数量…
• ⑵伽马分布（gamma）和指数分布（exponential）
• 间隔建模—车站问题
• 下一辆车可能什么时候到？
• 我的车到达还要多少时间？
• ⑶β分布和Dirichlet分布
• 小数建模
• ⑷Wishart分布—协方差矩阵的分布
  …

5.GLM

假设：
⑴y|x; θ ~ ExpFamily | η—（已η为自然参数的意思）
⑵给定x,目标为输出为E[ T( y）| x ]—T(y)为充分统计量
⑶想要达成 h(x)=E[ T( y）| x ]
⑷$η= θ^Tx$

---

伯努利：
$h_θ(x)=E(y|x;θ)=P(y=1|x;θ)=φ$
$φ={1\over{1+e^{-η}}}$
根据假设4而言，得到最终结果：
$φ={1\over{1+e^{-θ^Tx}}}$
正则响应函数：
$g(η)=E[y;η]={1\over{1+e^{-η}}}$
正则关联函数：$g^{-1}$

6.多项式分布（Multinomial）

y∈{1,…,k}

---

---

1.φ参数

$φ_1,φ_2,φ_3...φ_k$
$P(y=i)=φ_i$
因为$φ_k=1-(φ_1+φ_2...φ_{k-1})$
所以参数设定：$φ_1,φ_2,φ_3...φ_{k-1}$

2.T的定义

$$T_1={\left[\begin{matrix} 1 \\0 \\ \vdots \\0 \end{matrix} \right]}$$

$$T_2={\left[\begin{matrix} 0 \\1 \\ \vdots \\0 \end{matrix} \right]}$$

$$T_{k-1}={\left[\begin{matrix} 0 \\0 \\ \vdots \\1 \end{matrix} \right]}$$

$$T_k={\left[\begin{matrix} 0 \\0 \\ \vdots \\0 \end{matrix} \right]}$$

T∈$R^{k-1}$

I{True}=1
I{False}=0
I{2=3}=0
I{1+1=2}=1
即：$T（y）_i=I\{ y=i \}$

---

$P(y)=φ_1^{I\{y=1\}}φ_2^{I\{y=2\}}...φ_k^{I\{y=k\}}$
=$φ_1^{T(y)_1}φ_2^{T(y)_2}...φ_{k-1}^{T(y)_{k-1}}φ_k^{1-\sum_1^{k-1}T(y)_j}$
…
=$b(y)exp(η^TT(y)-a(η))$

---

η是一个向量

$$η={\left[\begin{matrix} {log{φ_1\overφ_k} } \\ \vdots \\{log{φ_{k-1}\overφ_k} } \end{matrix} \right]}∈{R^{k-1}}$$

---

$a(η)=-log(φ_k)$

---

b(y)=1

---

$φ_i={e^{η_i}\over{1+\sum_1^{k-1}e^{η_j}}}$

$η_i=θ_i^Tx$

这里就懒得代入公式了，手写的公式真烦…

---

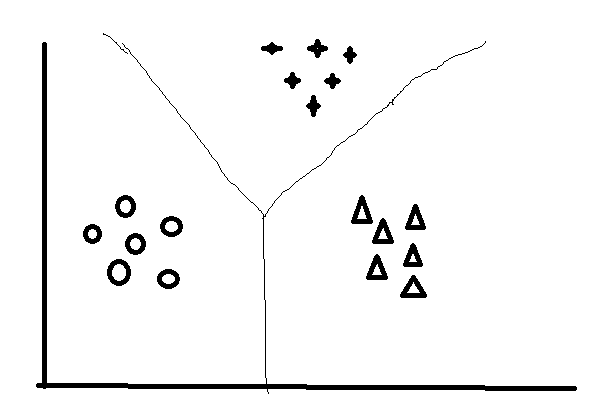
• softmax regression是logistic regression的推广