机器学习 牛顿法

参见https://blog.csdn.net/itplus/article/details/21896453

一.牛顿法

参见:https://zhuanlan.zhihu.com/p/33544363

1.概念:

"牛顿法"(Newton's method)是1种启发式的迭代算法,用于求解非线性最优化问题.其基本思想是:开始时随机选择1组参数(θ1,θ2...θn),在
该点处用多项式(下文均以2次为例)拟合目标函数,然后移动到该多项式的极值点处,并不断重复上述过程直到收敛.需要注意的是:仅当目标函数为
凸函数时梯度下降能保证找到全局最优解;其他情况下可能停留在驻点/无法收敛

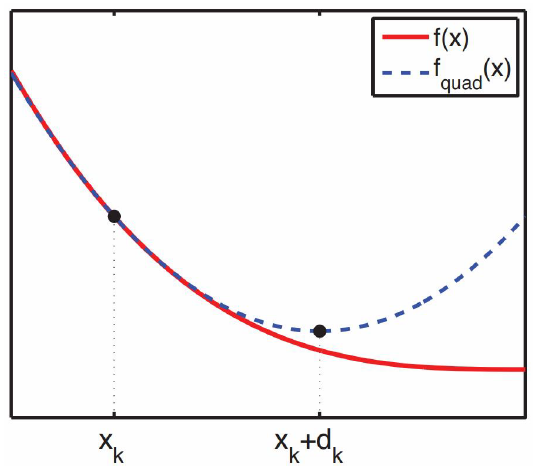
2.一般形式:

假设$H(J^{\prime }({\theta }^k;x_j))$非奇异,则将参数更新规则修正为$${\theta }^{k+1}=\theta ={\theta }^k-\alpha H^{-1}(J^{\prime }({\theta }^k;x_j))\nabla J({\theta }^k;x_j)$$其中α为学习率,后文均以$\alpha =1$为例.其搜索方向$d_k=-H^{-1}(J^{\prime }({\theta }^k;x_j))\nabla J({\theta }^k;x_j)$称为牛顿方向(Newton Direction)

3.推导:

若$J(\theta ;x_j)$二阶连续可导,将其在${\theta }^k$处泰勒展开得到$$J(\theta ;x_j)=J({\theta }^k;x_j)+\nabla {J({\theta }^k;x_j)}^T(\theta -{\theta }^k)+\frac{(\theta -{\theta }^k{)}^{T}H(J^{\prime }({\theta }^k;x_j))(\theta -{\theta }^k)}{2}+R_2(\theta )$$从而有$$\nabla J(\theta ;x_j$$