求两个数的最小公倍数方法汇总

方法一（普通方法）：

我们知道两个数的最小公倍数一定比这两个数都要大，假设我们要求的两个数为a和b，那么就可以从两个数中较大的那个数开始，用a和b除以他，直到这个数都能被a和b整除，就是我们要求的公倍数了。

如：4和6，较大的是6，4/6有余数，不符合。加一，4/7，4/6，都有余数，不符合。以此类推，加到12时，12/4，12/6，都能整除，即最小公倍数就是12。

转换成代码：

 方法二（简便法）：

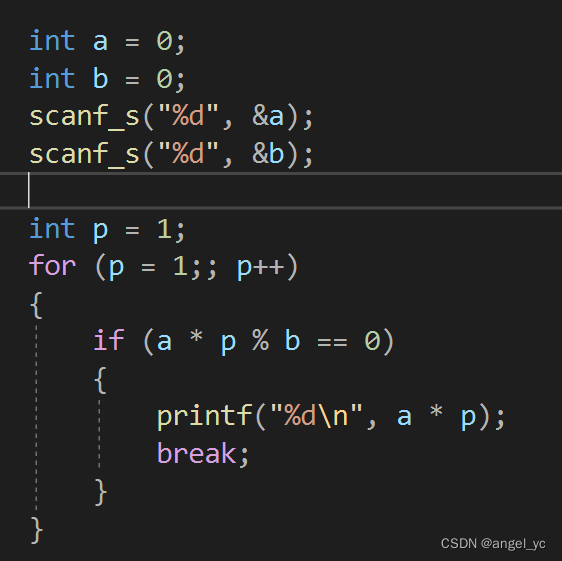
还是a和b，我们用一个由1开始的数p去乘以a的结果除以b，能整除那最小公倍数就是a*p

如：4和6，（1*4）/ 6 不能整除，（2*4）/ 6 不能整除，（3*4）/ 6 能整除，即最小公倍数是3*4=12.

转换成代码：

 方法三（借助辗转相除法）

以知a和b两个数，最小公倍数 = （a*b）/ 最大公约数

如：4和6的最大公约数是2，那最小公倍数就是（4*6） /  2 = 12。

转换成代码：

 这有几个细节需注意：

可能有人会觉得在代码中又定义M和N是多此一举，其实不然，如果不保留起始的a和b,在循环后a和b已经变了，这时再求出的结果必然是错误的。

这个辗转相除求最大公约数是有漏洞的比如12 和 24，这样两数成倍数关系的输出的是0；当然用个if()语句就能避免了

改进一下：

还有一点，我看很多帖子辗转相除还需去比较两数大小，其实没必要，如24和16，辗转相除24/16 = 1....8，16/8 = 2。最大公约数就是8，如果16和24，效果其实一样，16/24 = 0....16，24/16 = 1...8，16/8 = 2。