这篇文章 不保证你看了后一定会明白 欧拉公式,那么多数学专业的人深入浅出讲得比我好多了。但提供一种 从不明白到明白经过的一些步骤。如果你按这些步骤一步一步去做,先搞清什么,再搞清什么(可以从别的文章/知乎去弄明白),可能 最后就能看懂这个宇宙耍帅第一公式了 :)
本文不从泰勒展开角度来说明。
当x = 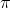 时:
时:
一:搞清sin/cos的意义 (可不只是三角形对边/斜边 邻边/斜边哦,要从单位圆旋转的角度来理解)
二:搞清弧度/角度的区别 ----这是为了理解,为什么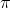 会出现在这个公式里,为什么指数中的值是
会出现在这个公式里,为什么指数中的值是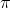 而不是其他值
而不是其他值
三:搞清e的特性 e的由来 同时对数 也绕不过的得配套弄明白 ----这是为了让你理解 ,为什么e会出现在这个公式里
四:了解指数函数 ----理解复指数的基础
五:搞清 复数的意义 ----进而理解复指数
下面分别补充一点信息吧
一:三角形sin/cos的意义 : 对边/斜边, 邻边/斜边 为什么不够? 几年前我是从自问自答这个问题开始的:钝角三角形的钝角 的sin值是哪条边 比 哪条边? 如果你得到的答案是其补角的sin,这只能说是机械记忆,还没理解透彻。
二:关键是要搞清:一度是一份,一个圆并不是只能分成360份,它还可以被分成362份。(只是大家约定俗成分成360份)这样每一度的大小是不固定的,依赖于我们把圆分成多少份。 而弧度的大小,就去除了这种量纲的影响,1弧度与数轴上的1的长度/大小相同,这样一个角有多大,就可以用数轴上的数(值为这个角的弧度)来表明了。用度数,做不到。欧拉公式如果不使用弧度来表示,则公式中,某个右上角, 会有一个小圆圈! 而只有用弧度,才能像现在这样简洁。
三:这个要说的就太多了。 先去搜那些讲得很好的文章/帖子吧。这里摘一点对我来说精华的句子:(感谢那么多前辈的分享)
"指数得到数量,对数得到时间。表示输入时间得到数量 ln(x)表示 输入数量 计算达到么多数量所需要的时间"
"如何理解对数? 一个直观的解释是:对数指的是达到某一数量 所需要的时间"
" = 增长 = e^增长数率*时间 =
" rate一般是小于等于1的,但time可以大于1
"任何一个数字,都可以 在某个时间 通过某个增长率来达到! 比如以的速度增长 9 =
这里面的ln9就是达到9这个数字的时间"
"也是这样,而且比球面更厉害 无论如何降维,
总是老样子,一点都没变,就好像你切掉孙悟空的一部分,你以为是一小片肉,睁眼一看,居然是另一个孙悟空,而且一样大!这种自相似或全息性太匪夷所思、太好玩儿了!"
四:略
五:同样 先去搜那些讲得很好的文章/帖子吧。这里摘一点对我来说精华的句子:(感谢那么多前辈的分享)
"如果数 1 表示向右移动 1 米的话,那么数 -1 就可以表示向左移动 1 米,数 i 可以表示向前移动 1 米,数 -i 可以表示向后移动 1 米,-1+i 可以表示向左前方移动 根号2 米。可见,虚数可以非常方便地描述二元事物"
"将实数a乘以i, 相当于将0 a 这个向量逆时针旋转90度, 所以乘以两个i就是旋转180度, 也就是变成了-a,所以i的平方等于-1"
将一个实数 加i 表示向实数轴垂直的方向 也就是虚数轴方向 前进1单位, 加2i表示前进两个单位。乘以i呢, 逆时针旋转90度; 乘i再乘i呢,逆时针旋转180度;i的3次方呢? 逆时针旋转270度;i的更多次方呢? 圆周旋转开始了。。 欧拉的远距离背影看到了吗? ---这句话可是我原创的 哈哈
举个栗子:=
次方 就是这个图上的A点 1就是角theta的弧度值
就是 90度角即
角
就是180度角即
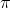 角
角
是不是能看到大神背影的轮廓了?
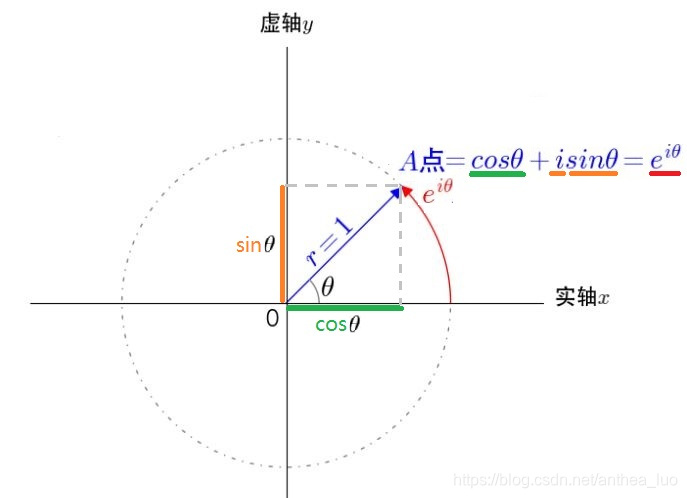
复指数: " f(z)=这个函数是可以定义在整个复数域上的,通过f(z)=f(x+iy)=
=
来定义,后面这个也叫欧拉公式。"
这个实数 我们取1, 也就是欧拉公式中的1. 1是这个单位圆的半径,是被旋转的数。旋转多少呢?旋转(无单位,弧度数值就是旋转的量),也就是半圆了。现在1有了,旋转需要的i有了,为什么指数中是
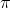 也来了。关键就差e了
也来了。关键就差e了
虽然我之前知道了e的特性,但在很长一段时间内我都不明白,欧拉公式中的e为什么一定是e,换成 2 3 5就不行? 仍然是知乎这条跟小学解释欧拉公式的回答启发了我: 怎么向小学生解释欧拉公式 e^(πi)+1=0? - 知乎
借酒老师的图: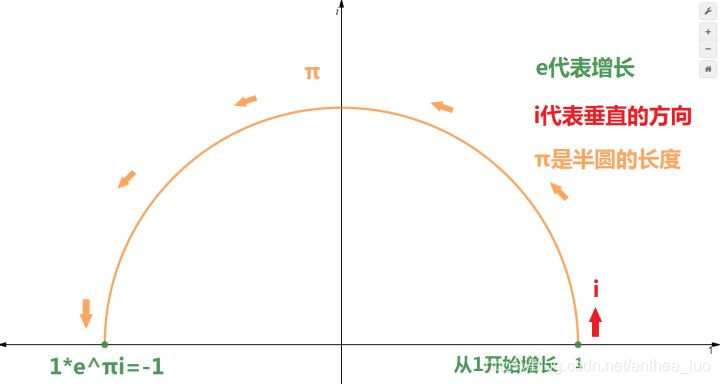
旋转,稍变通置换想一下, 也就是一种向某个方向的增长。既然是增长,就有增长的速度了。如果按全速 (单位时间增长率100%)增长/旋转 /跑路到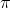 的结果,就到了起始点半圆的另一端,1的对面-1.
的结果,就到了起始点半圆的另一端,1的对面-1.
所以(再借一下图),桔色的线是以e为底 旋转的结果。如果底数换成2(或者说0.9e),可能的结果是浅蓝色的线;加和的结果>0;
如果底数换成3(或者说1.1e),可能的结果是深蓝色的线,加和的结果<0。只有以e的速度 增长,才会刚刚好落在-1点,加和结果为0! (请注意这张图可能是错的,原因见后面)(220702请注意这张图肯定是错的 加了一把红叉,正确的图在后面)

说完了,原来不明白的你,现在明白了吗? 没明白, 很好,我以前跟你一样。 没事,再多搜搜 想想,不行再晾晾再回来, 会明白的。念念不忘,可能有回响,哈哈
最近总算搞清了这个,比较开心。分享这个过程。 人一但明白了某些东西,就回不到不明白的时候。。。生活学习通用。。呵呵
"穿干净的衣 睡舒服的床 读有益的书 爱值得的人 "是我很喜欢的一句话,读来/想来都觉得温暖,分享给喜欢探索未知的你。嘿嘿
---------------------------------------------
190828补充:
最近小组分享欧拉公式,其他不熟悉欧拉公式的同学,最大的疑问是:为什么  可以代表旋转。他们可以理解 +i 以及 *i 能代表旋转;且 2 * 2 * 2 * 2 =
可以代表旋转。他们可以理解 +i 以及 *i 能代表旋转;且 2 * 2 * 2 * 2 = ok没问题,但
 为什么能代表旋转?看起来是i个e相乘 ? 不能用欧拉公式来证明,这样就是循环证明了。(
为什么能代表旋转?看起来是i个e相乘 ? 不能用欧拉公式来证明,这样就是循环证明了。( 是沿圆周运动ln2弧度,但这已经是运用了欧拉公式的结论)
好问题,我从来没这样想过...
--后来某天觉得最简单的回答可以是: 不要把指数上的i一定认为是(圆周)旋转,可以认为指数上的i 是运动.. 复数的乘法 结果还是复数,一直是在这个复平面上运动。
有两篇文章,可能可以解答:(主要还是看第二篇文章吧,更贴切这一个问题)
欧拉公式,复数域的成人礼_马同学图解数学的博客-CSDN博客 欧拉公式,复数域的成人礼
百度文库 复指数函数的定义问题 铜仁学院 孙小康徐松金
第一篇文章里:分别用极限/泰勒展开/导数的方式 来说明了。
用极限来理解 我觉得也比较好理解了,只要你愿意把x用替换,已经从普通的幂 联系到了复数乘法: 假设theta=1
=
n=3时:
n更大时,有更多个因子在相乘 乘的结果在一步步逼近 所在的点的位置。
所在的点的位置。用导数的方式来看,如果底数换成2或3 不能很好地代表旋转,甚至不能代表旋转,因为运动的速度 不像以e为底时,是垂直于的。 上面最后一张图 深蓝和浅蓝色的线 基本上也是错的,因为运动的速度和方向不是想象中那么好,可能在五度以内就跑到不知道什么方向去了,都不一定能到第二象限。。此图仅供初步理解想象
只有  才能代表圆周运动。
才能代表圆周运动。
第二篇文章 从解析函数 柯西黎曼条件的角度说明了 为什么复指数能与三角函数来。且文章的最后提到:欧拉公式 左边的e 只是一个符号,并不特指2.718..那个无理数。 也就是说 貌似可以写成这样:(这个加了删除线的,还是有问题,正确的请继续往下看)

但是当x = 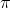 时:这个e肯定不能是其他值的。
时:这个e肯定不能是其他值的。
---------------------------------------
220702补充:
非常惭愧,对这些存留的疑问,有一天突然想到可以画图验证呀! 但是由于各种主观客观优化级的问题,拖到现在才来更新,十分对不住来学习的同学!
对于 代码及画出来的图如下:
分别使用 第5 第6 第7行中的一行 注释掉其他两行,画出来的三张图 如下:
import math
import matplotlib.pyplot as plt
# thetas = [0, 1, 2, 3 ...]
thetas = [int(x/10) for x in range(0, 201, 10)]
# thetas = [int(x/10) for x in range(0, 11, 10)]
# thetas = [int(x/10) for x in range(0, 21, 10)]
reals_images_e = []
reals_images_2 = []
reals_images_3 = []
for theta in thetas:
exponent_e = pow(math.e, complex(0, theta))
exponent_2 = pow(2, complex(0, theta))
exponent_3 = pow(3, complex(0, theta))
reals_images_e.append((exponent_e.real, exponent_e.imag))
reals_images_2.append((exponent_2.real, exponent_2.imag))
reals_images_3.append((exponent_3.real, exponent_3.imag))
plt.figure(figsize=(6, 6))
plt.scatter([x[0] for x in reals_images_e], [x[1] for x in reals_images_e], c="red", label="e")
plt.scatter([x[0] for x in reals_images_2], [x[1] for x in reals_images_2], c="blue", label="2")
plt.scatter([x[0] for x in reals_images_3], [x[1] for x in reals_images_3], c="green", label="3")
plt.plot([x for x in range(-1, 2, 1)], [0 for _ in range(-1, 2, 1)], c="grey", linewidth=0.2)
plt.plot([0 for _ in range(-1, 2, 1)], [x for x in range(-1, 2, 1)], c="grey", linewidth=0.2)
plt.legend()

先看这三张图中的第一张图,不管以e还是以2或以3为底,都是在做作圆周运动。
第二张图,右边(1, 0)的位置只看到一个绿色的点是因为红蓝点都被最后的绿色的点覆盖了。而以2为底的点 跑得较慢, 以3为底的点跑得较快。
第三张图类似。可以看到红绿之间的间隔在变大。因为这不是线性的速度,是指数级的数度。
以e以2以3为底的复指数,区别是什么? 是运动的速度!
对于 代码及画出来的图如下:
import math
import matplotlib.pyplot as plt
exponent_e_result = pow(math.e, complex(0, math.pi))
exponent_2_result = pow(2, complex(0, math.pi))
exponent_3_result = pow(3, complex(0, math.pi))
plt.figure(figsize=(5, 5))
plt.scatter(exponent_e_result.real, exponent_e_result.imag, c="red", label="e")
plt.scatter(exponent_2_result.real, exponent_2_result.imag, c="blue", label="2")
plt.scatter(exponent_3_result.real, exponent_3_result.imag, c="green", label="3")
plt.plot([x for x in range(-1, 2, 1)], [0 for _ in range(-1, 2, 1)], c="grey", linewidth=0.2)
plt.plot([0 for _ in range(-1, 2, 1)], [x for x in range(-1, 2, 1)], c="grey", linewidth=0.2)
plt.legend()
看到了吗? 只有以e为底的结果 落在(-1, 0)。 以2和以3为底的 结果不落在数轴上。
其实 还是这个论文里说到的问题: 复指数函数的定义问题 铜仁学院 孙小康徐松金 可以多看看这个。论文最后的部分说了:
因此 可以看成是 指数函数在复数域的自然推广
故可以定义 为复数域里的指数函数.
记为 或写成
。 这里注意 第一个e为一个符号,第二个e是极限值。


























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








