matlab实现图像逆滤波复原

        逆滤波是一种用于图像复原的滤波方法，其基本思想是将模糊图像通过反卷积的方式恢复成清晰图像。逆滤波器通常采用频域滤波方法，即将图像转化到频域中进行处理。

具体来说，逆滤波的操作过程分为两步：

1. 将被模糊的图像转化到频域：通过傅里叶变换或小波变换等方法，将原始图像的空间域表示转化为频域表示。

2. 对频域数据应用逆滤波器：构造一个逆滤波器，将模糊图像的频域数据进行反卷积处理，得到清晰的图像。通常会对逆滤波器进行加窗、截止等处理，以便控制滤波的效果。

        逆滤波的优点是能够实现比较精确的图像复原，适用于受到线性模糊（如运动模糊）的影响的图像。但是，逆滤波也有一些局限性，例如它对噪声的敏感性比较高，不能处理非线性模糊和噪声等问题。此外，逆滤波需要先知道图像的退化模型和点扩散函数等参数，否则会产生误差。

        因此，在实际应用中，逆滤波通常和其他图像复原方法结合使用，以便获得更好的处理效果。例如可以用逆滤波器估计原始清晰的图像，并结合Wiener滤波器进行频域平滑，去除高频噪声等。

close all;
clear all;
clc;
I=imread('lena.bmp');
I=rgb2gray(I);
%运动模糊示例
LEN=50;                                 %设置运动位移为50个像素
THETA=45;                               %设置运动角度为45°
PSF=fspecial('motion',LEN,THETA);       %建立二维仿真线性运动滤波器PSF
MF=imfilter(I,PSF,'circular','conv');   %用PSF产生退化图像
%消除匀速运动模糊
INITPSF=fspecial('motion',LEN,THETA);
[J,P]=deconvblind(MF,INITPSF,50);       %J复原图像，P复原点扩散函数
figure;
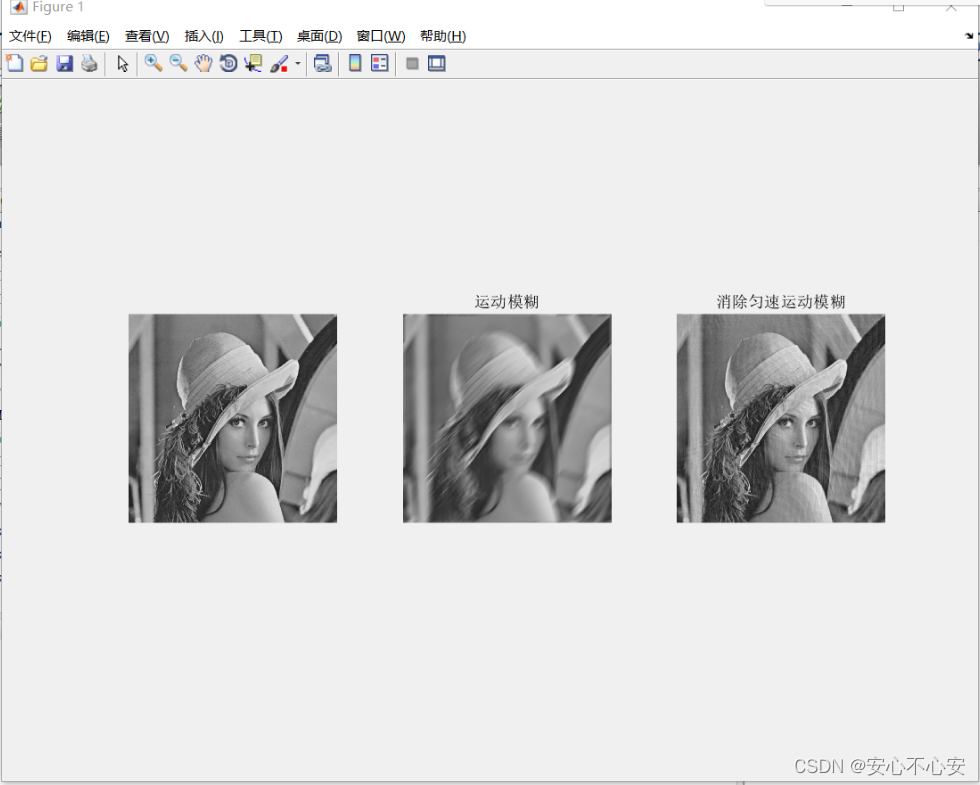
subplot(131),imshow(I);
subplot(132),imshow(MF),title('运动模糊');
subplot(133),imshow(J),title('消除匀速运动模糊');