复变函数公式大赏

B + +

已于 2023-08-03 23:13:03 修改

阅读量5.4k

点赞数 2

分类专栏：数学文章标签： python 数学

于 2021-08-27 19:12:14 首次发布

本文链接：https://blog.csdn.net/barry_wu_/article/details/119959269

版权

数学专栏收录该内容

12 篇文章 1 订阅

订阅专栏

基础

虚数单位的定义： $i=\sqrt{-1}$
复数： $z=a+bi=re^{iθ}$ ，实部为 $R e (z) = a$ ，虚部为 $I m (z) = b$
复数分为实数（b=0）和虚数（b≠0），实部为0的虚数为纯虚数
共轭复数： $\bar z=a-bi=re^{-iθ}$
模： $r=|z|=\sqrt{a^2+b^2}$
辐角： $θ=\mathrm{Arg}(z)=\arctan\frac yx+2kπ,k∈Z$
欧拉公式： $z=re^{iθ}=r(\cosθ+i\sinθ)$
复数的三角函数： $\sin z=\frac{e^{iz}-e^{-iz}}{2i},\cos z=\frac{e^{iz}+e^{-iz}}2,\tan z=-i·\frac{e^{iz}-e^{-iz}}{e^{iz}+e^{-iz}}$
反三角函数： $\mathrm{Arcsin}z=-i·\mathrm{Ln}(iz+\sqrt{1-z^2}),\mathrm{Arccos}z=\fracπ2+i·\mathrm{Ln}(iz+\sqrt{1-z^2}),\mathrm{Arctan}z=\frac i2·\mathrm{Ln}(\frac{1-iz}{1+iz})=\frac i2·[\mathrm{Ln}(1-iz)-\mathrm{Ln}(1+iz)]$
割函数： $\sinh z=\frac{e^z-e^{-z}}2,\cosh z=\frac{e^z+e^{-z}}2,\tanh z=\frac{e^z-e^{-z}}{e^z+e^{-z}}$
复数的对数： $\mathrm{Ln}(z)=\ln|r|+i\mathrm{Arg}(z)$
柯西-黎曼方程（C-R方程）： $\left\{\begin{matrix}u'_x=v'_y\\u'_y=-v'_x\end{matrix}\right.$ 。设 $z = x + y i ，$ 复变函数 $f (z) = u + v i$ ，则f(z)在满足上述方程组的情况下解析。
在某区域内解析的复变函数，其实部和虚部在该区域内也调和。

级数

设有复变函数 $f(z)=\sum_{i∈Z}a_i(z-z_0)^i$ 。对于复数列而言：

复数列级数收敛的判断方法和高等数学中实数列的完全一致
计算时，将求绝对值换为求复数的模
如果原函数按比值判别法、根式判别法等算出来的收敛圆中有奇点，则实际上的收敛半径为展开点到距其最近的奇点的距离
如果被展开点是展式的奇点，那就在其去心领域上
刚好在收敛圆上的点不一定收敛或发散
如果g(z)的值在f(z)展式的收敛圆内，则可以将g(z)代入f(z)的展式，变为f(g(z))
在幂级数的收敛圆内，幂级数的和函数解析

实函数可以被泰勒展开，复变函数则可以被洛朗展开：

洛朗展开就是在泰勒展开的基础上加上了负数次幂项
洛朗展式中的n次项系数为 $a_n=\frac1{2πi}∮_C\frac{f(z)}{(z-z_0)^{n+1}}\mathrm dz$
常见公式的展开方法可参考实函数展式
洛朗展开时，为了在指定区域内展开，有时需要将z换元成 $\frac1z$ 。在|z|<1时， $\frac1{1-z}=1+z+z^2+⋯$ 。若想要在|z|>1处将其展开，必须换元： $\frac1{1-z}=\frac1{z(\frac1z-1)}=-\frac1z(1+z^{-1}+z^{-2}+⋯)$
|z|≤1时， $\mathrm{Arctan}(z)=z-\frac{z^3}3+\frac{z^5}5-⋯$ 。|z|>1时不能直接泰勒展开，由 $\mathrm{Arctan}(z)+\mathrm{Arctan}(\frac1z)=\fracπ2$ 可得其洛朗展开为 $\mathrm{Arctan}(z)=\fracπ2-\mathrm{Arctan}(\frac1z)=\fracπ2-\frac1z+\frac1{3z^3}-\frac1{5z^5}+⋯$ 。

孤立奇点的性质：

若f(x)在z₀的洛朗展式中无负数次幂项，则z₀是可去奇点
既然可去，那么 $\lim\limits_{z→z_0}$ 存在（类似于“可去间断点”）
若f(x)在z₀的洛朗展式中最低次幂项为-n次，则z₀是n阶极点
极点处有 $\lim\limits_{z→z_0}f(z)=∞$ （类似于“无穷间断点”）
若f(x)在z₀的洛朗展式中有无数个负数次幂项，则z₀是本性奇点
$z→z_0$ 时，本性奇点处的函数值震荡（类似于“震荡间断点”）
z₀是f(x)的n阶奇点⇔z₀是 $\frac1{f(x)}$ 的n阶零点
将无穷远点∞作为孤立奇点时，用洛朗展式的正数次幂项系数判断其性质
零点阶数的判别方法可以参考不动点迭代法中的判别方法

积分

设有单连通域D和积分路径L。

若在单连通域内的实二元积分 $∫_L(P\mathrm dx+Q\mathrm dy)$ 满足 $P'_y=Q'_x$ ，则 $P\mathrm dx+Q\mathrm dy$ 为某一函数的全微分，且原积分的值与路径无关。同理，在处处解析的单连通域内， $∫_Lf(z)\mathrm dz$ 的积分也与路径无关。

L在D内成一元环C且f(z)在L内部解析时（内部为L的正方向的左侧）：

积分与路径无关，因此在不超出D，不改变路径所围奇点的的前提下可以随意变换路径C
柯西-古萨定理： $∮_Cf(z)\mathrm dz=0$
若C内有n阶奇点z₀，则 $∮_Cf(z)\mathrm dz=\lim\limits_{z→z_0}2πi·\frac{[(z-z_0)^nf(z)]^{(n-1)}}{(n-1)!}$ 或 $2πi·a_{-1}$ ， $a_{-1}$ 为 $z-z_0)^nf(z)$ 在 $z_0$ 点的洛朗展式的-1次幂的系数.
若C内有本性奇点z₀，则 $∮_Cf(z)\mathrm dz=2πi·a_{-1}$
若C内有n个孤立奇点，根据复合闭路定理，可以将C等价地变换成n元环，随后分解成n个对应的一元环，如下图：

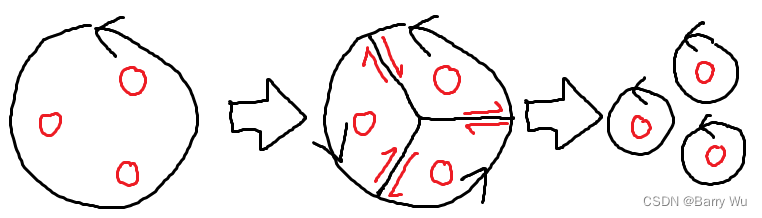
留数是去掉2πi后的围绕单个孤立奇点的一元环积分，即 $∮_Cf(z)\mathrm dz=2πiRes[f(z),z_0]$ 。

留数定理：若C内有z₁~z_n共n个奇点，由复合闭路定理可得 $∮_Cf(z)\mathrm dz=2πi\sum_{i=1}^nRes[f(z),z_i]$
$Res[f(z),z_i]=\lim\limits_{z→z_0}\frac{[(z-z_0)^nf(z)]^{(n-1)}}{(n-1)!}\underset{==========}{在z_0点展开}[(z-z_0)^nf(z)]_{-1}$
扩展留数定理：所有奇点的留数之和为0，即 $\sum_{i=1}^nRes[f(z),z_i]=-Res[f(z),∞]$ ，可在奇点很多时使用
$Res[f(z),∞]=Res[-\frac1{z^2}f(\frac1z),0]\\\sum_{i=1}^nRes[f(z),z_i]=Res[\frac1{z^2}f(\frac1z),0]$

以虚积实

积分时若有sin x、cos x，可考虑换元，令z=e^ix，则dz=ie^ixdx=iz dx， $_0^{2π}→∫_{|z|=1}$

若L为绕点z₀的，转角从α到β的圆弧，则有：

大弧引理： $\lim\limits_{r→+∞}∫_Lf(z)\mathrm dz=(β-α)i·\lim\limits_{z→∞}(z-z_0)f(z)$
小弧引理： $\lim\limits_{r→0^+}∫_Lf(z)\mathrm dz=(β-α)i·\lim\limits_{z→z_0}(z-z_0)f(z)$
约当引理： $\lim\limits_{z→∞}f(z)=0,m>0⇒\lim\limits_{r→0^+}∫_Lf(z)e^{imz}\mathrm dz=0$
互质因式积分定理：若P(x)和Q(x)是互质多项式，且Q比P高至少两次，Q(z)在实轴上不为0，则 $∫_{-∞}^{+∞}\frac{P(x)}{Q(x)}e^{imz}\mathrm dz=2πi·∑_{Im(A_i)>0}Res[\frac{P(x)}{Q(x)}e^{imz},a_i]$ ，m>0

from PIL import Image, ImageDraw
import matplotlib.pyplot as plt,numpy as np,time
def sin(z):return np.sin(z)#弧度
def cos(z):return np.cos(z)
def tan(z):return np.tan(z)
def csc(z):return 1/np.sin(z)
def sec(z):return 1/np.cos(z)
def cot(z):return 1/np.tan(z)
def asin(z):return np.arcsin(z)
def acos(z):return np.arccos(z)
def atan(z):return np.arctan(z)
def acot(z):return np.arctan(1/z)
def e(z):return np.exp(z)
def ln(z):return np.log(z)
def sinh(z):return np.sinh(z)
def tanh(z):return np.tanh(z)
def asinh(z):return np.arcsinh(z)
def atanh(z):return np.arctanh(z)
def arg(z):return np.angle(z)#弧度，从-π到+π
def Re(z):return z.real
def Im(z):return z.imag
e=np.e
π=np.pi
def to01(x):return (tanh(x)+1)/2#实数→0~1
def to1(x):return 1-e**(-x)#正数→0~1
def to255(x):return(int(255*(tanh(x)+1)/2))#实数域→0~255
def HSV2RGB(H,S,V):#弧度H，0~1S，0~1V→RGB255
    R,G,B=0,0,0
    if H>=0:h=H*3/π
    else:h=H*3/π+6
    i=int(h)%6
    F=h-i
    a,b,c=V*(1-S),V*(1-F*S),V*(1-(1-F)*S)  
    if i<1:  R,G,B=int(V*255),int(c*255),int(a*255)      
    elif i<2:R,G,B=int(b*255),int(V*255),int(a*255)      
    elif i<3:R,G,B=int(a*255),int(V*255),int(c*255)
    elif i<4:R,G,B=int(a*255),int(b*255),int(V*255)
    elif i<5:R,G,B=int(c*255),int(a*255),int(V*255)
    else:    R,G,B=int(V*255),int(a*255),int(b*255)
    return(R,G,B)
def RGB(R,G,B):return(to255(R),to255(G),to255(B))#RGB实数域→RGB255
def f(z,C):#迭代函数
    return asin(C)**(-z)
I=25 #迭代次数
name="3(asinC)^-z"#图名
Rx,Ry=2*π,2#区间最值
X,Y=3142,1000 #图像像素
pic=Image.new('RGB',(X,Y),'gray')
draw=ImageDraw.Draw(pic)

t0=time.time() #开始计时
for x in range(X):
    for y in range(Y):
        z0=(2*x/(X-1)-1)*Rx-(2*y/(Y-1)-1)*1j*Ry#坐标值
        z=z0#初值
        try:
            for i in range(I+1):
                z=f(z,z0)
                if abs(z)>10:break
            if abs(z)>10:#发散
                draw.point((x,y),'white')
                continue
            if abs(z)<1:draw.point((x,y),HSV2RGB(arg(z),1,(abs(z)*(2-abs(z)))**0.5))
            else:draw.point((x,y),HSV2RGB(arg(z),exp(1-abs(z)),1))
        except:continue
pic.save('Desktop/{}.png'.format(name),'PNG')#保存图像
print("已完成，用时{:.2f}秒".format(time.time()-t0))#显示用时