| Super A^B mod C |
| Time Limit: 1000ms, Special Time Limit:2500ms, Memory Limit:65536KB |
| Problem description |
| 计算A^B%C的结果,A^B是指A的B次方。 |
| Input |
| 多组测试数据,每组数据仅一行,分别为A,B,C的值。 A,B,C均为正整数。(1<=A,C<=1000000000,1<=B<=10^1000000). |
| Output |
| 对于每组测试数据,输出一行,为A^B%C的值。 |
| Sample Input |
3 3 34 4 4 |
| Sample Output |
00 |
有三个公式
1. 大整数取模
其实就是一个模运算转换了一下,就像下面这个例子
1234=((((0*10)+1)*10+2)*10+3)*10+4 mod n
由于只有*,+运算,可以将mod放进去 , 所以只需要,从最高位一位一位的×10取模就行了
2.欧拉定理扩展
首先欧拉定理
当a的指数很大的时候,可以推出
3.快速幂
代码如下
#include <iostream>
#include <cmath>
#include <cstring>
typedef long long llt ;
using namespace std;
int euler_phi(int n)
{
int m = floor(sqrt(n+0.5));
int ans = n;
for(int i = 2; i <= m; i++) if(n%i == 0){
ans = ans / i * (i-1);
while(n%i == 0)
n /= i;
}
if(n > 1) ans = ans / n *(n-1);
return ans;
}
//利用二进制计算a*b%mod
llt multiMod(llt a,llt b,llt mod){
llt ret = 0LL;
a %= mod;
while( b ){
if ( b & 1LL ) ret = ( ret + a ) % mod, --b;
b >>= 1LL;
a = ( a + a ) % mod;
}
return ret;
}
//计算a^b%mod
llt powerMod(llt a,llt b,llt mod){
llt ret = 1LL;
a %= mod;
while( b ){
if ( b & 1LL ) ret = multiMod(ret,a,mod),--b;
b >>= 1LL;
a = multiMod(a,a,mod);
}
return ret;
}
char big[1000050];
llt bigMod(int mod){
llt ret = 0;
int len = strlen(big);
for (int i = 0;i < len ;++i){
ret %= mod;
ret = ret * 10 + big[i]-'0';
}ret %= mod;
ret += mod;
return ret;
}
int main(){
llt a,b,c;
ios::sync_with_stdio(false);
while(cin>>a>>big>>c){
int er = euler_phi(c);
llt ans;
int len = strlen(big);
if ( len <= 10 ) {
b = 0;
for (int i = 0 ;i < len;++i)
b = b*10 + big[i]-'0';
ans = powerMod(a,b,c);
}
else {
b = bigMod(er);
ans = powerMod(a,b,c);
}
cout <<ans<<endl;
}
}








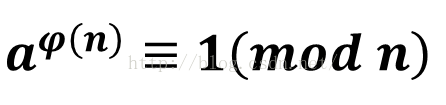
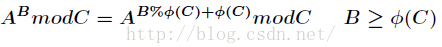














 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








