正规方程组(The normal equations)

2. 正规方程组

上一节的梯度下降是一种最小化成本函数$J$的方法。这一节我们将介绍另一种算法也可以实现该功能且不需要使用迭代。正规方程组通过计算成本函数对每个$\theta_j$的偏导数，求出偏导为零的点来成本函数的最小值。为了不必写大量的代数式和矩阵导数，让我们约定一些矩阵计算的符号。

---

2.1 矩阵导数

对于一个函数$f: \Bbb{R}^{m \times n} \to \Bbb{R}$，它将m*n的矩阵映射为一个实数，我们定义$f$对A的偏导为：

$$\nabla_Af(A) = \begin{bmatrix} \frac{\partial f}{\partial A_{11}} & \cdots & \frac{\partial f}{\partial A_{1n}} \\ \vdots & \ddots & \vdots\\ \frac{\partial f}{\partial A_{m1}} & \cdots & \frac{\partial f}{\partial A_{mn}} \\ \end{bmatrix}$$

举个例子，如果$A = \begin{bmatrix}A_{11} & A_{12} \\ A_{21} & A_{22}\end{bmatrix}$是一个2*2的矩阵，函数$f$定义如下：

$$f(A) = \frac{3}{2}A_{11} + 5A_{12}^2 + A_{21}A_{22}.$$

根据矩阵偏导公式可求得：

$$\nabla_Af(A) = \begin{bmatrix} \frac{3}{2} & 10A_{12} \\ A_{22} & A_{21}\\ \end{bmatrix}$$

---

我们引入矩阵的迹，写作“$\mathrm{tr}$”。对于一个n阶方阵A，它的迹是其对角线元素之和：

$$\mathrm{tr}A = \sum_{i=1}^n A_{ii}$$

如果a是一个实数（也可看成1-by-1矩阵），有$\mathrm{tr}a = a$。迹操作符有这样的性质：如果矩阵$A$和$B$满足$AB$是方阵，则有$\mathrm{tr}AB = \mathrm{tr}BA$，由此可推得：

$$\begin{align} \mathrm{tr}ABC = \mathrm{tr}CAB = \mathrm{tr}BCA\qquad\qquad\\ \mathrm{tr}ABCD = \mathrm{tr}DABC = \mathrm{tr}CDAB = \mathrm{tr}BCDA\\ \end{align}$$

迹操作符的下列性质也容易证明。其中$A$和$B$是方阵，$a$是实数：

$$\begin{align} \mathrm{tr}A &= \mathrm{tr}A^T\\ \mathrm{tr} (A + B) &= \mathrm{tr}A + \mathrm{tr}B\\ \mathrm{tr} aA &= a\mathrm{tr}A\\ \end{align}$$

结合矩阵的迹和矩阵导数，可以给出下列公式：

$$\begin{align} \nabla_A \mathrm{tr}AB &= B^T &(1)\\ \nabla_{A^T} f(A) &= (\nabla_{A} f(A))^T &(2)\\ \nabla_A \mathrm{tr}ABA^TC &= CAB + C^TAB^T \qquad \qquad &(3)\\ \nabla_A |A| &= |A|(A^{-1})^T &(4)\\ \end{align}$$

其中(4)只在矩阵A为满秩矩阵时成立。

---

2.2 二顾最小方差

了解了矩阵导数这一工具后，为了实现最小化$J(\theta)$的目标，我们先设法将成本函数$J$用向量表示。
给定一个训练集，我们将其以m-by-n矩阵$X$的形式表示，其中每一行代表一个训练样本：

$$X = \begin{bmatrix} -(x^{(1)})^T-\\ -(x^{(2)})^T-\\ \vdots\\ -(x^{(m)})^T-\\ \end{bmatrix}$$

同时将包含所有目标值的$\vec{y}$表示为一个m维的列向量：

$$\vec{y} = \begin{bmatrix} y^{(1)}\\ y^{(2)}\\ \vdots\\ y^{(m)}\\ \end{bmatrix}$$

因为$h_\theta(x^{(i)}) = (x^{(i)})^T \theta$，我们可以很容易地证明：

$$\begin{align} X\theta - \vec{y} &= \begin{bmatrix} (x^{(1)})^T\theta \\ \vdots \\ (x^{(m)})^T \theta \\ \end{bmatrix} - \begin{bmatrix} y^{(1)}\\ \vdots\\ y^{(m)}\\ \end{bmatrix}\\ &= \begin{bmatrix} h_\theta (x^{(1)}) - y^{(1)}\\ \vdots\\ h_\theta (x^{(m)}) - y^{(m)}\\ \end{bmatrix}\\ \end{align}$$

对于一个向量$z$，有$z^Tz = \sum_i z_i^2$，则：

$$\begin{align} \frac{1}{2} (X\theta - \vec{y})^T (X\theta - \vec{y}) &= \frac{1}{2} \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})^2 \\ &= J(\theta) \end{align}$$

最后要最小化$J$，我们要求解它关于$\theta$的导数：

$$\begin{align} \nabla_\theta J(\theta) &= \nabla_\theta \frac{1}{2} (X\theta - \vec{y})^T (X\theta - \vec{y})\\ &= \frac{1}{2} \nabla_\theta (\theta^T X^T X \theta - \theta^T X^T \vec{y} - \vec{y}^T X \theta + \vec{y}^T\vec{y})\\ &= \frac{1}{2} \nabla_\theta \mathrm{tr} (\theta^T X^T X \theta - \theta^T X^T \vec{y} - \vec{y}^T X \theta + \vec{y}^T\vec{y})\\ &= \frac{1}{2} \nabla_\theta (\mathrm{tr} \theta^T X^T X \theta - 2 \mathrm{tr} \vec{y}^T X \theta)\\ &= \frac{1}{2} (X^T X \theta + X^T X \theta - 2 X^T \vec{y})\\ &= X^T X \theta - X^T \vec{y}\\ \end{align}$$

为了最小化$J(\theta)$，我们要设法使其偏导数为零，这样就可推出正规方程：

$$X^T X \theta = X^T \vec{y}$$

那么权重矩阵$\theta$，应该调整为：

$$\theta = (X^T X)^{-1} X^T \vec{y}$$

---

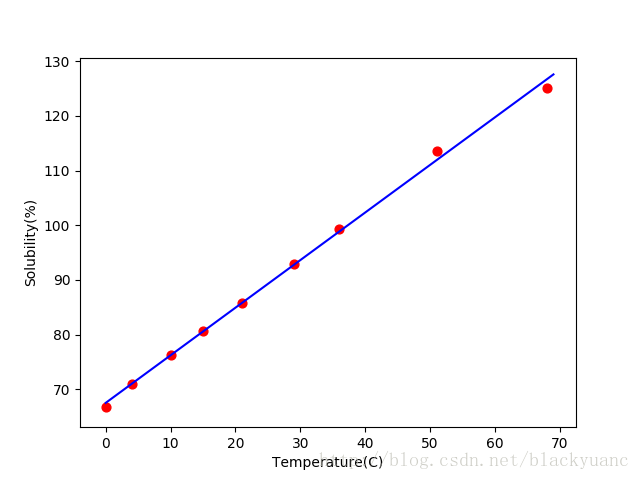
举个例子，硝酸钠的溶解度试验中，测得不同温度x（单位：C）下，硝酸钠溶解于水中的溶解度y%的数据如下：

温度	0	4	10	15	21	29	36	51	68
溶解度（%）	66.7	71.0	76.3	80.6	85.7	92.9	99.4	113.6	125.1

求$y$和$x$的经验回归函数。

从上面的数据中可以，写出输入特征矩阵$X$和目标变量矩阵$\vec{y}$。

$$\begin{align} X &=\left[ \begin{matrix} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1\\ 0 & 4 & 10 & 15 & 21 & 29 & 36 & 51 & 68\\ \end{matrix} \right]^T \\ \vec{y} &= [ \begin{matrix} 66.7 & 71.0 & 76.3 & 80.6 & 85.7 & 92.9 & 99.4 & 113.6 & 125.1 \end{matrix} ]^T \\ \end{align}$$

代入公式$\theta = (X^T X)^{-1} X^T \vec{y}$中求解权重$\theta$的值，得：

$$\theta_0 = 67.5078, \qquad \theta_1 = 0.8706$$

于是所求的线性回归假设为：

$$y = 67.5078 + 0.8706x.$$

下图将训练样本和回归函数绘制在一起：

实现的python代码如下：

# coding=utf-8
import matplotlib.pyplot as plt
import numpy as np

# 输入特征温度和标签溶解度
X = np.array([0 , 4, 10, 15, 21, 29, 36, 51, 68])
y = np.array([[66.7, 71.0, 76.3, 80.6, 85.7, 92.9, 99.4, 113.6, 125.1]])
# X转化为n*1的矩阵
X_0 = np.ones(len(X)).astype(dtype=np.int)
X_new = np.array([X_0, X])

# 根据求参数公式theta = (X.T * X)^-1 * X.T * y求解
temp = np.matrix(np.dot(X_new, X_new.T))
ans_matrix = temp ** -1 * X_new * y.T
# 训练后的模型，提取截距和系数
intercept = np.array(ans_matrix)[0][0]
coef = np.array(ans_matrix)[1][0]
# x从0到70，y=ax+b
lx = np.arange(0, 70)
ly = coef * lx + intercept

# 绘制拟合直线
plt.plot(lx, ly, color='blue')
# 绘制数据点和x轴y轴标题
plt.scatter(X, y, c='red', s=40, marker='o')
plt.xlabel('Temperature(C)')
plt.ylabel('Solubility(%)')
plt.show()

在特征维度少的情况下，正规方程组的计算会比梯度下降法快很多，推荐计算线性回归时多使用该方法。