FPGA图像处理13_常用算法_图像放大

图像放大

此处只说明图像放大，不涉及图像缩小，因为大多数图像处理场景下图像缩小的需求可以直接使用像素点抽取的方式实现，而且在缩小之后还涉及到与需求关联紧密的图像拼接，很难有通用化的设计。

算法原理

坐标转换

图像放大有以下关键设计：

1. 坐标转换：输出图像像素点坐标转化为输入图像内的坐标，并找到包围该坐标的像素点用于插值计算。
2. 数据缓冲：输入图像数据截取与缓冲，将用于插值计算的像素点值缓冲，并且在缓冲（FIFO）将满时向数据流上游反压。
3. 插值计算：常用的图像放大插值计算有双线性插值（BiLinear）和双立方插值（BiCubic），前者计算简单，但是会造成图像模糊（相当于低通滤波）；后者计算复杂，但是比较好的保留了图像边缘。
4. 参数传递：由于算法实现涉及到多级数据缓冲及非均匀的流水线处理，而且参数在各个缓冲阶段都需要使用，因此在各级缓冲及流水线处理时都需要使用该处理阶段专用的参数，并且在输入1帧图像数据前更新。如果所有缓冲和计算流水线都共用一组参数的话，则会造成上级缓冲参数更新完成时，下级缓冲还在处理前一帧图像的数据。

以下设计场景是将输入图像内指定范围的图像子块放大至与输入图像相同的分辩率。

图像放大的计算参数包括：

• 图像子块的左上角顶点在输入图像内的坐标：(x₀, y₀) 浮点值；
• 图像子块内像素点的间距：z 浮点值，以输入图像内相邻像素点间距为 1，表示图像子块内像素点的间距，由于是放大计算，z<1，且图像放大倍数为 $\frac{1}{z^2}$；
• 用于插值计算的输入图像的像素点坐标范围：x_begin、x_end、y_begin、y_end，全部为整数值，用于截取输入图像数据。

令输入图像分辩率为 $W\times H$，由 (x₀, y₀) 和 z 计算得到全部计算参数，不同的插值算法有不同的参数计算。

双线性插值，使用包围当前输出像素点（绿点）的 4 个输入像素点（红点）进行插值。

一般情况：

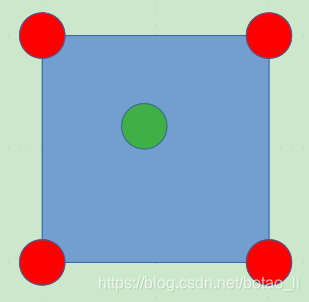
特殊情况，输出像素点与输入像素点的左上角点重合。

即输出像素点与某个输入像素点重合情况下的特殊处理，可以选择 4 个输入像素点中任一点作为重合点，但是由于图像坐标系由左上角开始，因此与左上角点重合比较便于计算。

$$\begin{gathered} x_{begin}\le x_0 \\ {x}_{begin}=floor(x_0) \end{gathered}$$

$$\begin{gathered} y_{begin}\le y_0 \\ {y}_{begin}=floor(y_0) \end{gathered}$$

输出图像的列坐标最大值为 $x_0+(W-1)\times z$

输出图像的行坐标最大值为 $y_0+(H-1)\times z$
$$\begin{gathered} x_{end}>x_0+(W-1)\times z \\ {x}_{end}=floor(x_0+(W-1)\times z+1) \end{gathered}$$

$$\begin{gathered} y_{end}>y_0+(H-1)\times z \\ {y}_{end}=floor(y_0+(H-1)\times \end{gathered}$$