Jensen不等式
其实在运筹学以及基础的优化理论中,便有涉及。设f是定义域为实数的函数,如果对于所有的实数x,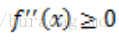
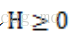
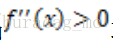
Jensen不等式表述如下:
如果f是凸函数,X是随机变量,那么
特别地,如果f是严格凸函数,当且仅当
(也就是说X是常量时),
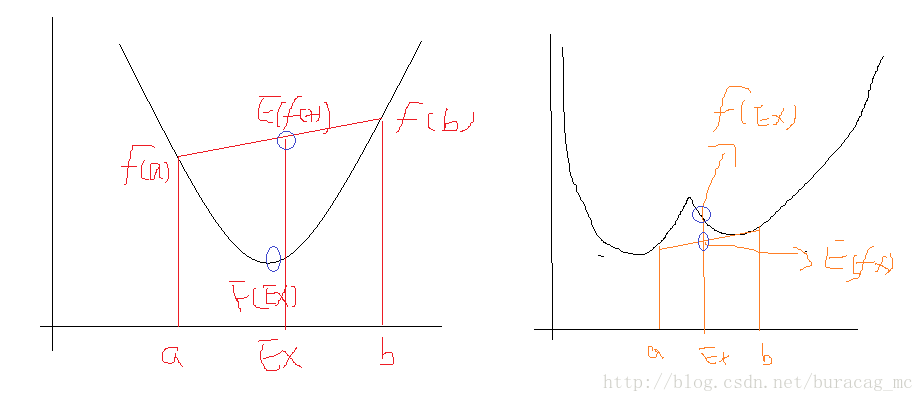
成立,画一个草图可以直观地看出:
可以看到,左图是符合我们对于凸函数的定义的,右图则不符合。
同理我们可以知道,当Jensen不等式应用于凹函数时,不等号变向,即 E[f(X)]≤f(EX) 。
最大似然估计
在讲解EM算法之前,还需要最大似然估计的相关知识。
假设我们需要调查学校的男生的身高分布。我们进行简单随机抽样(当然,分层抽样啊,整群抽样都是OK的~),随机抽选了100个男生作为抽样样本。然后得到的100个样本值。假设他们的身高(对应的男生总体)是服从高斯分布(总体分布)的。但是这个分布的均值u和方差
σ2
我们不知道(总体分布的参数未知),这两个参数就是我们要估计的。记作:
用数理统计的语言表达出来便是,我们独立地按照概率密度p(x|θ)抽取100样本组成样本集X,我们想通过样本集X来估计出未知参数θ。这里假设概率密度p(x|θ)我们知道了是高斯分布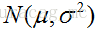
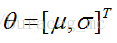
这个联合概率反映了,在概率密度函数的参数是 θ 时,得到样本集X的概率。因为这里X是已知的,也就是说我抽取到的这100个人的身高可以测出来,也就是已知的了。而 θ 是未知了,则上面这个公式只有 θ 是未知数,所以它是 θ 的函数。这个函数表示的是在不同的参数 θ 取值下,取得当前这个样本集的可能性,因此称为参数 θ 相对于样本集X的似然函数(likehood function)。记为 L(θ) 。
极大似然估计,是一种概率论在统计学的应用,它是常见的参数估计的方法之一。其是建立在这样的思想上:已知某个参数能使这个样本集出现的概率最大,我们当然不会再去选择使得这个样本集出现的概率较小的参数,所以干脆就把这个参数作为估计的真实值。
比较拗口哈~,不过理解起来还是比较容易的。就拿前面的例子说,如果参数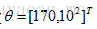
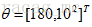
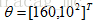
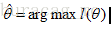
但通常为了便于分析,可以取对数得到对数似然函数,
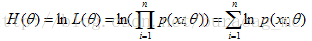
即:
好了,现在我们知道了,要求解θ,只需要使θ的似然函数L(θ)极大化,然后极大值对应的θ就是我们的估计。这里就回到了求最值的问题了。怎么求一个函数的最值呢?当然,在存在解析解的情况下,我们直接求其偏导数并令其为0即可得出;
但是在不存在解析解或者直接求解比较困年的情况下,我们通常是采取梯度下降(上升)法来进行求解的,例如典型的LR的参数求解中便是利用了梯度下降法;又SVM在求解的实现时,利用SMO求解时,是同时对两个拉格朗日乘子进行梯度上升法(由于SMO是求解max W(a),详见博文http://blog.csdn.net/buracag_mc/article/details/76762249),同样利用迭代来求解的。这里不是本文的侧重点,故不再展开赘述了。
大概总结一下,求解最大似然函数估计值的一般步骤:
求得联合概率密度,写出似然函数;
对似然函数取对数,并整理;
求偏导数,并令其为0,得到似然方程;
求解似然方程,得到的参数即为所求。
EM算法
给定的训练样本集,样本间独立,我们想找到每个样例隐含的类别z,能使得p(x,z)最大。p(x,z)的最大对数似然估计如下:
利用似然估计求解的思想。
求得似然函数
取对数,得到对数似然函数
对每个样例的每个可能类别z求联合分布概率和。
但是直接求 θ 一般比较困难,因为有隐藏变量z存在,但是一般确定了z后,求解就容易了。
EM是一种解决存在隐含变量优化问题的有效方法。既然不能直接最大化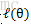
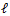
对于每一个样本
xi
,让
Qi
表示该样例隐含变量z的某种分布,
Qi
满足的条件是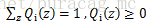
讲的比较抽样哈?没关系,继续用小例子来说明:
对于第二部分讲的似然估计的内容,我们要估计的只有一个总体的参数(即学校男生的身高分布参数);但是如果我们要同时估计男生和女生的身高分布情况呢?
我们改变一下假设,同时随机选取100个男生和100个女生混在一起,得到一个样本值后(即身高值),我们不知道是从男生的那个身高分布中选取的,还是从女生的那个身高分布中选取的。对于每一个样本,我们就有两个东西需要进行估计的了:
其一是这个人是男生还是女生?
其二是男生和女生对应的身高的高斯分布的参数是多少?
这里假设隐藏变量z是身高,那么隐藏变量对应的分布就是连续的高斯分布。如果隐藏变量z是男女,那么就是伯努利分布了。这样讲,应该是比较容易理解隐藏变量的意思了。
下面我们假设隐藏变量z是男女,可以由前面阐述的内容得到下面的公式:
(1)式到(2)式没问题,就是分子分母同乘以一个相等的函数,这里即是隐藏变量的概率密度函数。(2)式到(3)式利用到了第一部分讲的Jensen不等式,首先考虑到
log(x)
是凹函数。
就是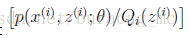
即将自变量看成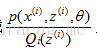
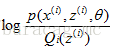
这个过程可以看作是对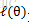
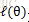
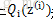
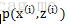
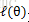
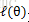
按照这个思路,我们要找到等式成立的条件。根据Jensen不等式,要想让等式成立,需要让随机变量变成常数值,即:
c为常量,不依赖于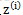
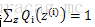
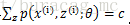
至此,我们推出了在固定其他参数
θ
后,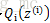
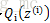
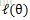
接下来的便是M步,就是在给定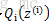
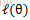
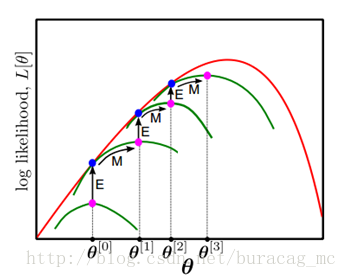
那么一般的EM算法的步骤如下:
初始化分布参数 θ ;
重复以下步骤直到收敛:
- E步骤:根据参数初始值或上一次迭代的模型参数来计算出隐性变量的后验概率,其实就是隐性变量的期望。作为隐藏变量的现估计值:
- M步骤:将似然函数最大化以获得新的参数值:
- E步骤:根据参数初始值或上一次迭代的模型参数来计算出隐性变量的后验概率,其实就是隐性变量的期望。作为隐藏变量的现估计值:
如何确保EM的参数估计值收敛呢?假定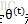
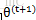
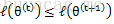
详细证明可以参考博客【2】
最终会得到证明结果:
这样就证明了会单调增加。一种收敛方法是不再变化,还有一种就是变化幅度很小。
OK,我们将EM算法的思想用到我们这部分的例子上:
首先我们初始化参数 θ ,男生的总体分布参数
,女生的总体的分布参数
;
然后我们将200个样本值分别计算出隐藏变量的后验概率,作为隐藏变量的现估计值。即在样本 xi 的取值下,该样本属于男生的后验概率是多少,属于女生的后验概率是多少,并将该样本划分到后验概率最大的那类去。即E步。
将200个样本划分给男生和女生完成后,重新根据对应的样本,参照我们第二部分的内容,做极大似然估计,得到更新后的参数 θ 值。即M步
重复二、三步,直到收敛
最后,输出男生和女生对应总体分布的参数值。
参考资料如下:
【1】>http://ju.outofmemory.cn/entry/148394
【2】>http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006936.html
【3】>http://blog.csdn.net/zouxy09/article/details/8537620/
【4】>《大数据挖掘与统计机器学习》- 吕晓玲 宋捷 - 中国人民大学出版社










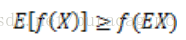
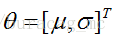
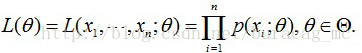
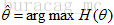
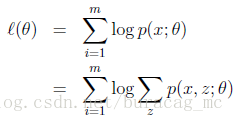
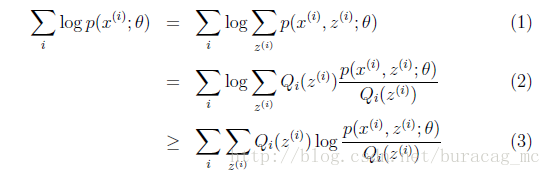
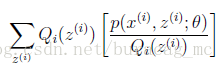
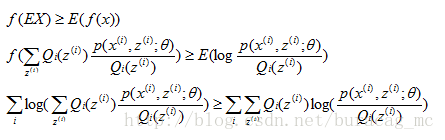
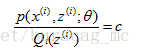
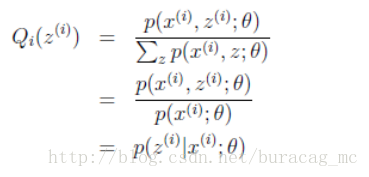
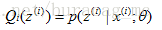
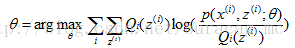
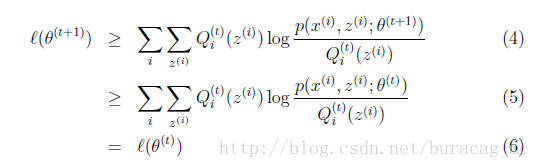













 4万+
4万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








