10-1:Logistic Regression Problem
Logistic回归问题
我们举一个心脏病预测的例子 ,我们根据患者的年龄,性别,体重,血压这些特征来预测这个人是否有心脏病,很显然这是一个二分类的例子,其输出结果为{+1,-1},算法流程如下图所示:
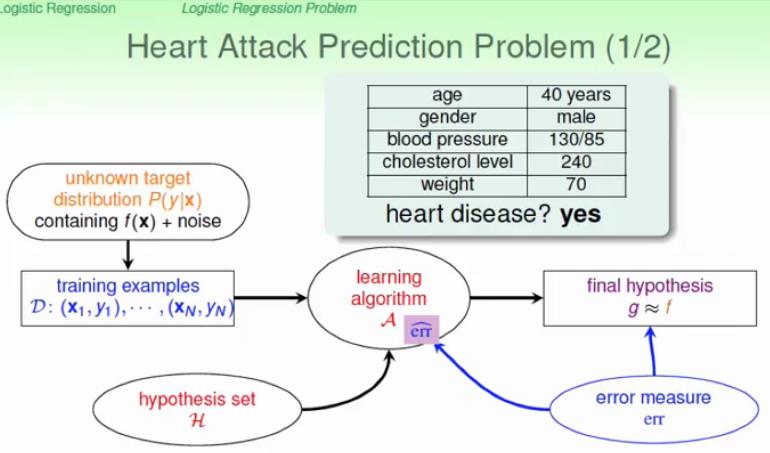
具体流程图的介绍在第八节已经详细介绍了,这里就不再赘述了。
那么我们如何根据这些特征判定是否该患者患心脏病呢?类似PLA,我们一般可以取一个阈值threshold=0.5,然后计算目标分布
p(y|x)
的大小,当
p(+1|x)>0.5
时就认为患有心脏病,否则就认为没有心脏病,即目标函数:
f(x)=sign(p(+1|x)−12)∈
{-1,1}
但是如果我们考虑的不是该患者患病与否,而是考虑这个患者患心脏病的几率是多大的?因为我们通常告诉患者的是他患病的概率是多大,那么我们就需要重新定义一个目标函数了,如下式所示:
f(x)=p(+1|x)∈[0,1]
上面通常称为软二元分类(soft Binary classification),那么对于这种分类,我们想要的理想数据格式应该是如下所示(即我们想要的是确切的概率 p):

但是实际的数据,比如医院给你病例数据之类的,肯定不会是上面这种完美的数据,因为医院肯定只会记录该患者是否患病,实际的数据应该像下面这样:

比如上面第一条记录了O,表示是患病的,第二条记录了
×
,表示没有患病。并没有直观的给出我们想要的目标函数分布(即患病概率)。我们将这种数据可以作为理想的数据+noise共同生成的。
那么我们接下来就应该寻找一个好的hypothesis来尽可能的接近目标函数
f(x)
。
例如,输入
X=(x0,x1,x2,…xd)
个病人的输入特征,我们可以根据PLA的思想,构建一个风险分数(risk score)S来对该患者患病的程度进行量化,即:
S=∑di=0wixi
,但是我们知道概率是有上界的,不会超过1,如果单单使用S来进行评判,并不能达到我们想要的结果,我们应该将S进行转换,最常用的转换方式就是sigmoid函数了,即:
θ(S)=11+e−s
,该函数对应的函数图像如下图所示:
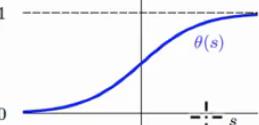
从函数图像可以看出sigmoid函数是平滑的S形曲线,并且是递增的,那么我们可以将上面的
S=∑di=0wixi=wTx
带入sigmoid函数,就可以将S映射到[0,1]区间,也就得到了我们想要的概率p,这一结果可以定义为Logistic Hypothesis即:
h(x)=θ(wTx)=11+e−wTx
然后我们就可以用h(x)来近似目标函数分
f(x)=p(y|x)
了。
10-2:Logistic Regression Error
Logistic回归错误衡量
回想一下我们学过的线性分类(Linear classification)、线性回归(Linear Regression),以及今天学到的Logistic Regression。我们将他们进行对比如下图所示:
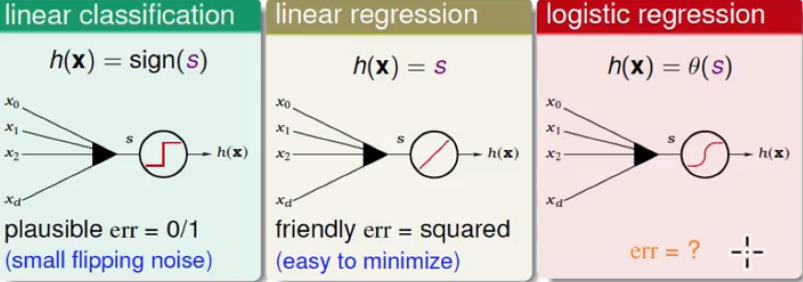
我们很容易能够得到图中的
S=wTx
,即三种假设h都有着共同的得分函数。如何衡量他们的误差呢?线性分类用的是0/1 error,线性回归用的是Squared error(平方错误),那么问题来了,对于Logistic Regression,我们该如何量化它的误差(即
Ein(w)
)。
我们的目标函数
f(x)=p(+1|x)
,我们可以将其等价为公式(1):
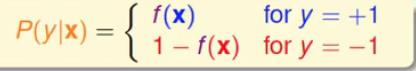
我们考虑一组数据
D=(x1,O),(x2,X)…(xN,X)
(O代表+1,X代表-1),那么实际能产生这一组数据的概率是多大呢,其计算过程如下:
p=p(x1)p(O|x1)×p(x2)p(X|x2)×⋯×p(xN)p(X|xN)
(将公式(1)带入)
=p(x1)f(x1)×p(x2)[1−f(x2)]×⋯×p(xN)[1−f(xN)]
我们考虑以下两个问题:
1. 我们的目的是找到一个最好的Hypothesis近似等于f(x),那么上面的p理论上由f(x)产生的和h(x)产生的是差不多大的概率(不然就是不好的hypothesis)
2. 上面的数据D是一个正常的数据,那么f(x)产生D的概率p应该是足够大的
综合2条规则,我们可以得到下面g:
g=argmaxh likelihood(h)
即
f=h
,并且最大化g。
由于
h(x)=θ(wTx)
,或者从sigmoid函数我们可以看出
h(−x)=1−h(x)
,这样子就能代替掉p中的(
1−h(x)
),计算过程如下:
likelihood(h)=p(x1)h(x1)×p(x2)h(−x2)×⋯×p(xN)h(−xN)
实际中我们假设先验概率p(x)是相等的,进一步推出:
在Lecture 9中我们就用w替换掉了h,这里一样如此,并且将
h(x)=θ(wTx)
带入:进一步推出:
两边取对数
ln
,进一步推出:
maxh∑Ni=1lnθ(ynwTxn)
=minw1N∑Nn=1[−lnθ(ynwTxn)]
将
θ(S)=11+exp(−S)
,进一步推出:
=minw1N∑Nn=1[ln(1+exp(−ynwTxn))]
将上式和经常使用的误差公式对比一下:
误差公式
minw1N∑Nn=1err(h(xn),yn)
我们最终得到Logistic Regression的交叉熵错误(cross_entropy error):
err(w,x,y)=ln(1+exp(−ynwTxn))
10-3:Gradient of Logistic Regression Error
Logistic回归误差的梯度
上一节我们已经求出来了
Ein(w)
的表达式:
minwEin(w)=1N∑Nn=1[ln(1+exp(−ynwTxn))]
那么我们接下来的目的便是最小化这个函数来得到权值向量w。我们考虑
Ein(w)
的函数图像:

我们发现,
Ein(w)
具有可微分、连续、二阶可微、并且还是凸函数。由于
Ein(w)
是凸函数,我们可以直接可以求
∇Ein(w)=0
,然后得到w的解。
因为
Ein(w)
的表达式还是有点复杂的,我们首先进行如下替换:
我们进行如下求微分的计算过程(由于太复杂,就直接盗用图片,然后在下面进行解释。)
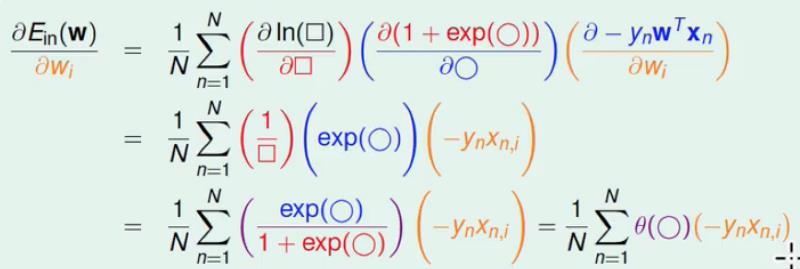
这里求微分的计算是分布计算的,可以类似于:
∂E∂w=∂E∂t1∂t1∂t2⋯∂tn∂w
(其实,你类似于乘法相乘是很容易理解的)。
为了简便,这里我们将得到的
xn,i
用
xn
表示,得到最终的梯度公式如下:
∇Ein(w)=1N∑Nn=1θ(−ynwTxn)⋅(−ynxn)
Lecture9中,介绍了何时能使得
Ein(w)
最小,即梯度为0的时候(因为这是凸函数),我们考虑两种情况:
1. 所有的
θ(−ynwTxn)=0
,这个条件可以满足梯度为0,但是当且仅当
ynwTxn>>0
,换个角度想也就是数据是Linear Separable(线性可分)的。
2. 当数据线性不可分的时候,我们又不能像LinReg(线性回归)一样使用闭式解,那么这种问题怎么解呢?其实可以用迭代的方法。
回顾一下之前PLA的算法过程:

我们找到一个错误记为
(xn(t),yn(t))
,并且用这个错误点来对w进行修正,具体细节在Lecture2中有详细介绍。
上面的修正错误的过程,我们如果换一个角度看呢?
wt+1←wt+1⋅[sign(wTx≠yn)]⋅ynxn
这个式子和上面算法的修正是一样的,只是做了一些小小的改变:

如图中
η和v
所示,
η
一般称之为学习的步长,v称为学习的方向。上面的这种方法我们称为iterative optimization approach(迭代优化算法)。
10-4:Gradient Descent
梯度下降
我们回顾一下
Ein(w)
的函数图像:
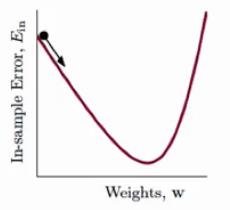
我们将
Ein(w)
比作一个山谷,那么假定我们现在处于小球的位置,那么如何才能最快的到谷底呢?我们需要考虑走的方向v和每次走的步长
η
,有一个贪婪的方法是在
η
给定的情况下,条件限制为
||v||=1
,即:
min||v||=1Ein(wt+ηv)
其中
wt+1=wt+ηv
,我们接下来简化这个过程,利用taylor展开式:可以得到:
min||v||=1Ein(wt+ηv)≈Ein(wt)+ηvT∇Ein(wt)
(这里有一个想法就是:我觉得这就相当于求直线斜率的表达式把即:
min||v||=1Ein(wt+ηv)−Ein(wt)ηvT=∇Ein(wt)
,将步长限制的比较小的时候,那么直线可以等价于曲线的)。
那么经过上面的简化之后,我们发现
Ein(wt)
是常数,
η
是给定的正数,那么现在就只剩下一个变量v了,那么上式就转化为:
min||v||=1vT∇Ein(wt)
要使这个表达式值最小,因为这是内积,那么v的方向和
∇Ein(wt)
的方向相反的话就会得到最小值,即:
v=−∇Ein(wt)||∇Ein(wt)||
得到方向v之后,利用我们上一节课得到iterative optimization approach(迭代优化算法),即
wt+1←wt+ηv
,当
η
很小的时候,带入式子可得:
wt+1←wt−η∇Ein(wt)||∇Ein(wt)||
上面的式子就是经典的Gradient Descent (梯度下降)算法。
从上面式子可以看出,现在只剩下如何选择
η
了。下面观察一下
η
对GD(梯度下降)的影响:
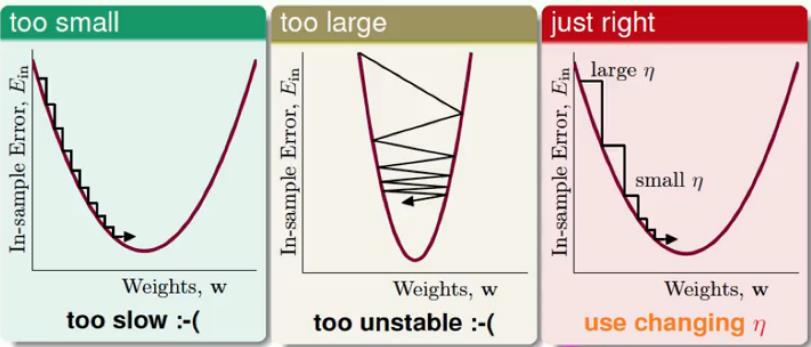
1. 我们发现,小的
η
能够收敛到最小值,但是收敛速度太慢了
2. 大的
η
下降非常不稳定,甚至还可能出现越下降越高的情形
3. 最右边的是比较好的
η
,它在梯度比较大(即坡比较陡)的时候,
η
比较大,在梯度比较小(即坡比较缓)的时候,
η
比较小,很完美的收敛,即
η
和梯度的大小成正比。
我们下面重新定义一下梯度下降公式:

图中红色的
η
和紫色的
η
是不一样的,它们之间存在的关系为:
紫色
η=(红色η)⋅1||∇Ein(wt)||
我们将最终得到的紫色
η
称为固定的学习速率。
综上,我们对Logistic回归算法进行小结:

1. 先初始化w_0
2. 计算每依次迭代过程中梯度
∇Ein(wt)
的值
3. 用梯度下降算法对
wt+1
进行更新
直到
∇Ein(wt+1)≈0
或者足够的迭代次数后使得循环结束,返回最后的
wt+1
作为g。
注明:
文章中所有的图片均来自台湾大学林轩田《机器学习基石》课程









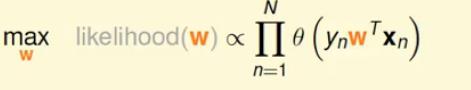
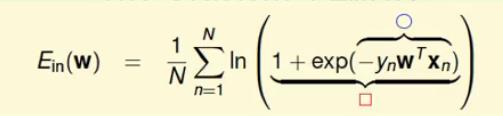














 3570
3570











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








