台湾大学机器学习基石Lecture7

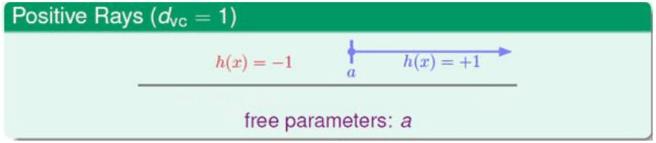
7-1:Definition Of VC-Dimension

vc维的定义
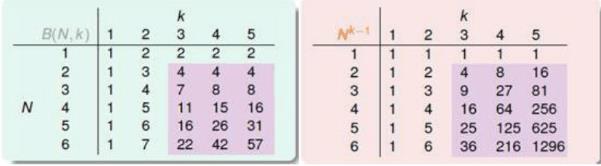
上一节我们介绍了成长函数$M_H(N)$、上限函数$B(N,K)$、以及上限函数小于等于一个组合$\sum_{i=0}^{k-1}C_N^i$，由组合知道，其最高次幂为$N^{k-1}$，下面用两张图来介绍上限函数作为成长函数和$N^{k-1}$作为成长函数的差别：

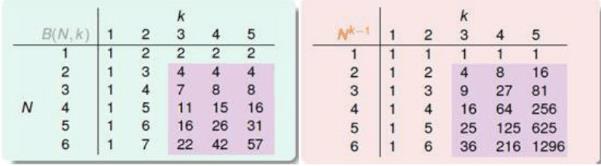
从图中可以看出当$N\geq 2 and K\geq 3$时候，$M_H(N)=B(N,K)\leq N^{k-1}$,由上一个Lecture最后一个小节有如下不等式：
$P[|E_{in}(h)-E_{out}(h)|>\xi]\leq 4\cdot M_H(2N)\cdot exp(-\frac{1}{8}\xi^2N)$
将$M_H(N)\leq N^{k-1}$带入上式得到：
$P[|E_{in}(h)-E_{out}(h)|>\xi]\leq 4\cdot (2N)^{k-1}\cdot exp(-\frac{1}{8}\xi^2N)$
假设存在三个条件：

1. 成长函数$M_H(N)$存在断点K
2. 样本数量N足够大
3. 算法A能够选择一个g，使得$E_{in}(g)$很小

那么由上面的不等式+三个条件的限制，就能够保证机器学习是可行的。
这一节我们介绍一个新的朋友-VC-Dimension。
VC维就是指假设空间能够被二分类样本最大分类的输入点数目。例如，上一节中2-D Perceptron中，当输入为$(x_1,x_2,x_3)$三个输入时，可以被分成下面的情况：

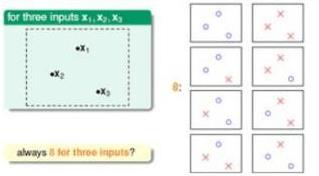
也可能是下面的情况：

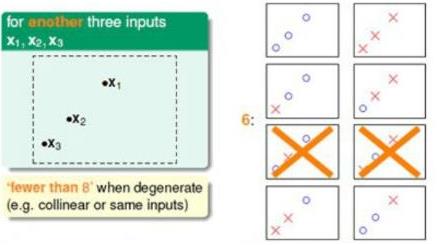
两幅图的区别在于输入的样本点分布不同，导致结果不同。第一张图片可以被完全二分类，第二张图片不能被完全二分类（即被分为$2^{N}$种），现在定义一个符号$d_{vc}$，它表示所能分类的最大输入样本点数目。如上图，虽然有些输入情况不能被完全二分类，但是只要至少一种输入分布能够被分为完全二分类，那么就是$d_{vc}$,例如上面图中$d_{vc}=3$(这边没有显示输入是4种情况的时候，Lecture5已经叙述了是不能被完全二分类的。)所以$d_{vc}$可以定义为：
$d_{vc}='最小的k'-1$
定义了$d_{vc}$，那么就存在下面两种情况：

1. 当$N\leq d_{vc}\rightarrow$N个输入可以被完全二分类。
2. 当$N> d_{vc}\rightarrow$假设空间一定存在一个断点K

使用VC维重写成长函数的上限，如下式：
如果$N>2,d_{vc}>2\rightarrow M_H(N)\leq N^{d_{vc}}$
对上一节介绍的常用分布进行VC维对比：

类型	vc维	断点k
正射线	$d_{vc}=1$	k=2
正的间隔	$d_{vc}=2$	k=3
凸集合	no	no
2-D感知器	$d_{vc}=3$	k=4

那么如果$d_{vc}$有限，g就能够得到泛化保证（即$E_{in}(g)\approx E_{out}(g)$）

---

7-2:VC-Dimension of Perceptrons

感知器的vc维。
考虑2-D Perceptron，例如使用PLA算法，假设数据D是线性可分的，那么可以运行足够的循环就能使得$E_{in}(g)=0$,并且假设输入数据集和总体数据集分布相同，那么由VC维保证，就可以使得$E_{out}(g)\approx 0$，二维可以，那么如果维数更高呢？
我们从具体情况考虑，再推向一般。

• 1-D感知器，由之前的推导，其成长函数$M_H(N)=2N$,可以推出$d_{vc}=3-1=2$
• 2_D感知器，由上面可知$d_{vc}=3$

所以，能否假设$d_{vc}=d+1?$(实际是对的)
下面对这个进行等式进行证明，要证明这个等式，相当于证明它的等价条件：
1. $d_{vc}\geq (d+1)$,即证明有（d+1）个输入可以被完全二分类。
2. $d_{vc}<(d+2)$,即证明任何（d+2）个输入不能被完全二分类。
首先证明1：
因为只需要找出一种（d+1）个输入能被完全二分类即可，假设输入向量为：
假设第一个输入向量为全0$（0,0\ldots ,0）$,第二个向量为第一个输入为1，其他为0即$（1,0\ldots ,0）$，依次类推，第（d+1）个输入向量为最后一个输入为1，其它为0即：$（0,0\ldots 0,1）$，由PLA，参数是[（d+1）+1]个，因为还有一个threshold对应的$x_0$，那么加上$x_0=1$，可以得到下面的输入向量矩阵：

显然，上面X的行列式值为1，所以X是可逆的。我们要使得(d+1)个输入能被完全二分类，即$y=(y_0,y_1,y_2\ldots ,y_{d+1})$有$2^{d+1}$种情况(因为$y_0$是阈值，是一个不变的值，所以只有$2^{d+1}$种)，我们知道，正确分类的时候，$sign(XW)=Y$,那么如果$XW=Y$,当然满足上面的情况，因为X是可逆的，那么$W=X^{-1}Y$，即无论Y什么情况，都有相对应的W，所以1得证。
下面证明2：
我们以2-D感知器为例，考虑下图的输入：

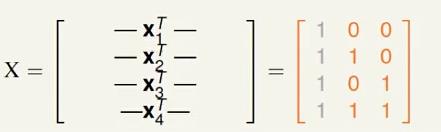
假设在标记的时候，标记$y_1=-1,y_2=1,y_3=1$，那么$y_4$不可能为1，因为
$x_4=x_3+x_2-x_1$，两边同时乘以w也不会引起变化，得到
$w^Tx_4=w^Tx_3+w^Tx_2-w^Tx_1>0$一定成立（在满足$y_1=-1,y_2=1,y_3=1$），这种关系在线性代数中其实就是线性相关，导致了不可能完全二分类。考虑（d+2）个输入：

那么一定有$x_{d+2}=x_{d+1}+\ldots +x_2-x_1$,也就是，其实也就是这（d+2）组数据肯定线性相关，那么总有一个$y_n$必须为其他的y表示，也就是不可能达到$2^{d+2}$种。所以2成立。
综上：可得$d_{vc}=d+1$

---

7-3:physical intuition of VC-Dimension

vc维的物理直觉
因为数据样本D的维度和参数W的维数是一致的，考虑下面两种情形：


图一$d_{vc}=1$，对应的参数也就一个a即边界的确定，图二中$d_{vc}=2$，那么对应的参数为2即上下边界。首先给出一个新的概念-自由度，$w=(w_0,\ldots ,w_d)$是假设空间的自由度，由此可以推断出:自由度和$d_{vc}$的大小是相等的。VC维的物理意义就是在做二元分类的时候能够有多少的自由度，也就是能将假设空间最大可分的数量。

• 这边的自由度即参数个数，当然参数越多，模型也就越复杂，也就是$d_{vc}$越大，那么使得$E_{in}(g)\approx E_{out}(g)$不成立的坏数据就会变多。为了避免这种情况，就只有使得输入样本数N变大，才能保证$E_{in}(g)\approx E_{out}(g)$。

回顾一下之前的问题：
1. 是否能够保证$E_{in}(g)$足够小
2. 是否能偶保证$E_{in}(g)\approx E_{out}(g)$
不同的VC维情况如下：

小的VC维	大的VC维
1不能够保证，因为选择太少了	1能够保证，因为有很多的选择
2能够保证，由变换后的霍夫丁不等式可以保证	2不能保证，同样由霍夫丁不等式说明

注：上面表格提到的变换后的霍夫丁不等式：
$P[|E_{in}(h)-E_{out}(h)|>\xi]\leq 4\cdot (2N)^{d_{vc}}\cdot exp(-\frac{1}{8}\xi^2N)$
由公式可以看出，选择一个恰当的$d_{vc}$或者说H是很有必要的。

---

7-4:interpreting VC-Dimension

vc维的解释
vc维限制的公式如下：
$P[|E_{in}(h)-E_{out}(h)|>\xi]\leq 4\cdot (2N)^{d_{vc}}\cdot exp(-\frac{1}{8}\xi^2N)$
设不等式右边为$\delta$,那么下面的式子必定成立：
$P[|E_{in}(h)-E_{out}(h)|\leq \xi]\geq 1-\delta$
并且有：
$\delta=4\cdot (2N)^{d_{vc}}\cdot exp(-\frac{1}{8}\xi^2N)$
$\rightarrow \xi=\sqrt{\frac{8}{N}\cdot ln(\frac{4\cdot(2N)^{d_{vc}}}{8})}$
其中$E_{in}(g)-E_{out}(g)$的大小称为泛化误差（Generalization error），并且
$|E_{in}(g)-E_{out}(g)|\leq \xi$
$\rightarrow\ \ E_{in}(g)-\sqrt{\frac{8}{N}\cdot ln(\frac{4\cdot(2N)^{d_{vc}}}{8})} \leq E_{out}(g)$
$\leq E_{in}(g)+\sqrt{\frac{8}{N}\cdot ln(\frac{4\cdot(2N)^{d_{vc}}}{8})}$
我们一般关心的错误的上限，将不等式右边定义为$\Omega(N,H,\delta)$,表示模型复杂度。观察下面图形：

图中，蓝线表示$E_{in}(g)$,红线代表模型复杂度，紫线代表$E_{out}(g)$,从图中可以看出，$E_{in}(g)$随着$d_{vc}$的增大而降低（因为选择多了），模型复杂度随着$d_{vc}$的增大而增大（因为参数变多了），$E_{out}(g)$随着$d_{vc}$先下降后上升,那么这里就存在一个最优的$d_{vc}^*$。因此寻找最优的$d_{vc}^*$就很重要了。
这里其实还有一个问题，其实VC Bound是很宽松的，比如上限$N^{d_{vc}}$本就是一个很宽松的值。从下面一幅图也能看出来。

举个例子：
假设给定$\xi =0.1,\delta=0.3,d_{vc}=3$，求N为多少能满足下面的式子：
$\delta\geq 4\cdot (2N)^{d_{vc}}\cdot exp(-\frac{1}{8}\xi^2N)$如下图所示：

即$N\approx 30000，即N\approx 10000d_{vc}$时，才能有比较好的模型，其实是因为上限过于宽松导致的，实际上并不需要这么大，在实际应用中，$N\approx 10d_{vc}$