台湾大学机器学习基石Lecture6

6-1:Restriction of Break point

断点的限制
上一节介绍了成长函数$M_H(N)$，即样本为二元分类的情况下，假设空间在N个样本点上能够产生的最大二分数量。由此引出了断点（Break Point）的概念，即不能满足完全分类，也就是k个输入样本点，无论k怎么分布，都不能被shatter为$2^k$种情况，那么k就是断点。
我们进一步对K进行讨论，假设k=2时：

• 当输入N=1时，很容易得到$M_H(N)=2$

• 当输入N=2时，由于断点为2，所以不能四种情况即{OO,OX,XO,XX}都满足，（如果都满足的话断点就不是2了），得到$M_H(N)<4$(最大的成长函数为3)

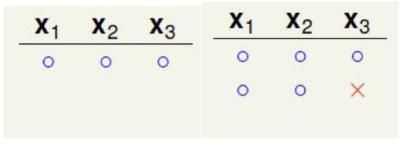
• 当输入N=3时，情况比较复杂，用图片的形式展示：
  
  
  
  从六张图片可以看出，最大的成长函数$M_H(N)=4$，再多加一种分类情况都会导致断点数目不是2（其实很好理解，因为$(x_1,x_2,x_3)$从全O到每一个都唯一存在一个X，下面继续加分类的话肯定会产生XX的情况，这样子就会产生{OO,OX,XO,XX}，就不满足断点=2的限制了）。
  从上面可以看出，断点k的大小很大的程度上限制了成长函数$M_H(N)$，下面举个特殊的例子。
  比如k=1，也就是断点为1，那么成长函数的情况会是什么样子呢？我们知道，断点为1就只能是O或者X两者中任意一种情况，很显然，N=1时，只能是O和X,N=2时，只能是XX和OO$，依次类推\ldots$，最后对于所有的N，$M_H(N)=1$

---

6-2:Bounding Function

这一节我们提出一个新的概念——上限函数B(N,K)，它的意思就是在给定具体断点的情形下来考虑成长函数的最大值的情形。
提出上限函数的好处在于：给定断点k之后，不用考虑假设空间是哪一种。例如B(N,3)，它可表示一维PLA，也可以表示positive interval(正的间隔)（因为2个假设的断点都是3），我们只需要计算出上限函数，用上限函数来对成长函数进行约束。其中k表示断点数为3，由上节的推导很容易得到B(N,3)的值也就是上限函数的值为7。
那么我们就有了一个新目标，即证明：
$B(N,K)\leq poly(N)$(poly表示多项式)
如果不等式成立，那么我们就可以证明机器学习是可行的，因为$M_H(N)\leq B(N,K)$,我们先考虑B(N,K)的分布情况，然后从中概括出一般规律。上限函数的部分值如下表所示：

对其中对角线上的元素作说明，由上一节知，断点为 $K$ 时，$B(K,K)= (2^k-1)$,因为如果再加一种分类情况，断点数就不是k了。

---

6-3:B(N,K)-Inductive cases

B(N,K)的归纳情形
归纳得出一般性的求解B(N,K)的公式为：
$B(N,K)\leq B(N,K-1)+B(N-1,K-1)$，即个值小于等于其正上方的值和其左上方的值之和，这个结论在数学中是比较常见的。
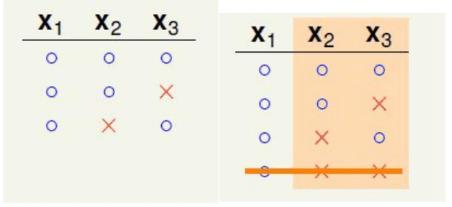
下面用一个例子说明一下，假设考虑B(4，3)，由公式有$B(4,3)\leq B(3,3)+B(3,2)$,编程实践结果如下图：

对这幅混乱的图换一个方式展示出来：

从图中可以看出，上面8种情况$x_1,x_2,x_3$分别是一模一样的，$x_4$是以O和X的方式成对出现。考虑二分类，设橙色部分一共有$\alpha$个二分类，紫色部分互不相同，考虑优有$\beta$个分类，则
$B(4,3)=2\alpha + \beta$
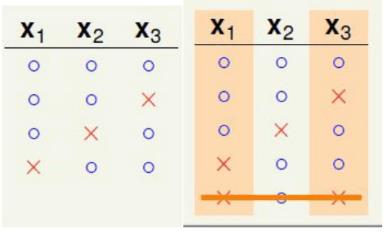
心现在考虑k=3的情形，同样像上面的那种情形排序：

我们发现，这种分类情形就相当于去掉$x_4$以后将8中情形合并以后得到的$\alpha$，而$\beta$是不变的，可以得到：
$\alpha + \beta \leq B(3,3)$
下面对$\alpha$单独考虑，如下图：

很明显由上一节可以得出，$\alpha \leq B(3,2)$
综上：$B(4,3)=2\alpha + \beta\leq B(3,3)+B(3,2)$
最后得到的上限函数的计算结果表格如下：

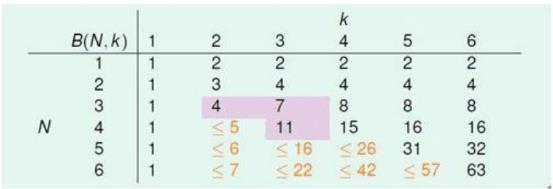
由$B(N,K)\leq B(N,K-1)+B(N-1,K-1)$计算得到：
$B(N,K)\leq \sum_{i=0}^{k-1}{C_N^i}$,从表达式可以看出，上限函数的最高次幂为$N^{k-1}$,可以得到结论，对于给定的K：
$M_H(N)\leq B(N,K) \leq \sum_{i=0}^{k-1}{C_N^i}$

---

6-4:A Pictorial Proof

图案证明
我们最开始因为$M\rightarrow \infty$，p[BAD D]的概率趋于很大，造成误差很大，所以在第五节中讲述用$effective(N)$来代替M，即二分空间并进而得到了成长函数$M_H(N)\leq 2^N$,我们想要的是多项式形式的成长函数而不是指数函数，因为这样子函数收敛的更快，所以由此引出了断点K，并得到了$M_H(N)\leq N^{k-1}$，从而得到了多项式形式的上限。理想的霍夫丁不等式如下：
$p[\exists h \in H s.t|E_{in}(h)-E_{out}(h)|>\xi]\leq 2M_H(N)exp(-2\xi^2N)$
但是实际上的结果存在一点偏差：
$p[\exists h \in H s.t|E_{in}(h)-E_{out}(h)|>\xi]\leq 2\cdot 2M_H(2N)exp(-2\cdot \frac{1}{16}\xi^2N)$
我们发现两个式子相比，下面的式子分别多出了一个2，成长函数多出了一个2倍，指数上多出来一个$\frac{1}{16}$。
下面从三个方面进行说明（证明难度太大了）:

• Step1:$p[\exists h \in H \ s.t|E_{in}(h)-E_{out}(h)|>\xi]\leq p[\exists h \in H s.t|E_{in}(h)-E'_{in}(h)|>\frac{\xi}{2} ]$
  虽然$E_{in}(h)$是有限的，但是 $E_{out}(h)$是无限的，所以下面就是要使得$E_{in}(h)$变成有限的。
  我们另取N个点称为$D'$，用这N个点来估计$E'_{in}(h)$，下图显示了$E'_{in}(h)$和$E_{in}(h)$的关系：
  
  我们使得$E'_{in}(h)$和$E_{in}(h)$关于$E_{out}(h)$对称分布，那么$E_{in}(h)-E_{out}(h)|>\xi$的概率是要小于等于$E_{in}(h)-E'_{in}(h)|>\frac{\xi}{2}$的概率的。（这里不是很明白）

• Step2:$p[\exists h \in H \ s.t|E_{in}(h)-E_{out}(h)|>\xi]\leq2\cdot 2M_H(2N) p[fixed \ h\ s.t|E_{in}(h)-E'_{in}(h)|>\frac{\xi}{2} ]$
  因为上面加入了另外$D'$数据，那么有限H就变为$|H(x_1,\ldots x_N,x'_1,\ldots x'_N)|$,所以成长函数的上限应该变为$M_H(2N)$,带入公式可得到上式。

• Step3
  考虑罐子和小球的例子，以前罐子里面的小球是无限多个，现在变为2N个，从罐子中取出N个，剩下的就是$D'$，并且：
  $E_{in}(h)-E'_{in}(h)|>\frac{\xi}{2} =E_{in}(h)-\frac{E'_{in}(h)+E_{in}(h)}{2}|>\frac{\xi}{4}$
  推出：$p[\exists h \in H \ s.t|E_{in}(h)-E_{out}(h)|>\xi]$
  $\leq 2\cdot 2M_H(2N) p[fixed \ h\ s.t|E_{in}(h)-E'_{in}(h)|>\frac{\xi}{2} ]$
  $\leq 2\cdot 2M_H(2N) p[fixed \ h\ s.t|E_{in}(h)-\frac{E'_{in}(h)+E_{in}(h)}{2}|>\frac{\xi}{4}$
  $\leq 2\cdot 2M_H(2N)exp(-2\cdot \frac{1}{16}\xi^2N)$
  由此，得到了一个机器学习中著名的理论：vapnik-Chervonenkis bound。
  假设用2D感知器，其断点为4，成长函数上限为$O(N^3)$,如果取得的N足够大，那么由这个理论就可以得到：用算法选取比较小的g（也就是$E_{in}$比较小），那么在test数据集上也会是出现比较小的差错，那么就证明了机器学习是可能的。