《Fundamentals Of Computer Graphics》虎书第三版翻译——第六章 矩阵变换

线性代数的机制可以用来表达在3D场景中排列对象、用摄像机观察它们并将它们放到屏幕上所需的许多操作。几何变换，如旋转、平移、缩放和投影可以通过矩阵乘法来完成，而用于实现这一目的的变换矩阵是本章的主题。我们将展示一组点如何转换，如果这些点被表示为从原点出发的偏移向量，并且我们将使用图6.1所示的时钟作为点集的一个示例。把时钟想象成一堆点它们是矢量的端点它们的尾巴在原点。我们还讨论了这些变换对位置(点)、位移向量和表面法向量的不同作用

6.1 2D线性变换

我们可以使用一个2 × 2矩阵来改变或变换一个2D向量:

这种运算是一个线性变换，它取一个2维向量，然后通过一个简单的矩阵乘法得到另一个2维向量。

通过这个简单的公式，我们可以实现各种有用的转换，这取决于我们在矩阵中放入的元素，就像下面几节将要讨论的那样。出于我们的目的，考虑沿x轴移动为水平移动，沿y轴移动为垂直移动。

6.1.1 缩放

最基本的变换是沿着坐标轴的缩放。这个变换可以改变长度和可能的方向:

注意这个矩阵对一个带有笛卡尔分量(x, y)的向量做了什么:

通过观察轴向比例矩阵我们可以读出两个比例因子。
例如。将x和y一致缩小1 / 2的矩阵是(图6.1)

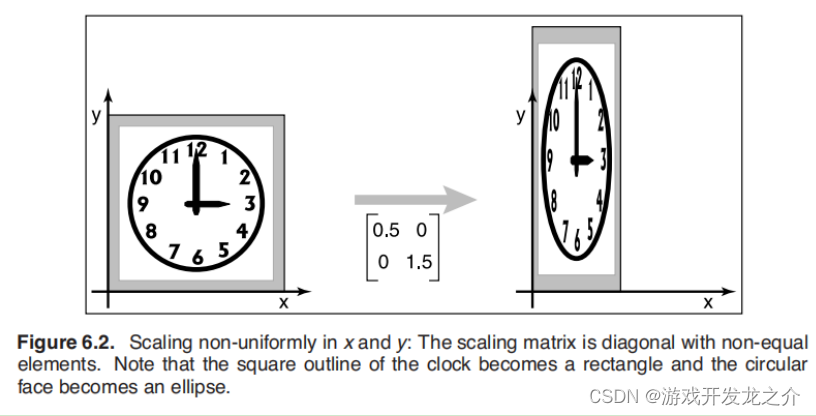
一个矩阵可以水平缩放一倍，垂直缩放三倍(看图6.2)

6.1.2 切变

切变是一种你向侧面推东西，产生的效果类似一副你用手推过的牌;底部的卡片保持不变，卡片被推的越远，他们就越接近扑克的牌堆顶。水平和垂直切变矩阵为

（事实上，圆在任何矩阵变换下的图像都是椭圆。）
在这两种情况下，切变时钟的方形轮廓变成平行四边形，而切变时钟的圆形表面变成椭圆形。
另一种考虑切变的方法是只考虑垂直(或水平)轴的旋转。取垂直轴并使其顺时针倾斜一个角度φ的剪切变换是

同样地，同样，水平轴逆时针旋转角度φ的切变矩阵为

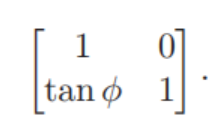
6.1.3 旋转

假设我们想逆时针旋转向量a一个角φ以得到向量b(图6.5)。如果a与x轴成α角，它的长度是r = x2a + y2a，我们知道

因为b是a旋转产生的，所以它的长度也是r。因为b与a旋转了一个角φ，所以b与x轴形成一个角(α + φ)。使