Monarch矩阵：计算高效的稀疏型矩阵分解

©PaperWeekly 原创 · 作者 | 苏剑林

单位 | 科学空间

研究方向 | NLP、神经网络

在矩阵压缩这个问题上，我们通常有两个策略可以选择，分别是低秩化和稀疏化。低秩化通过寻找矩阵的低秩近似来减少矩阵尺寸，而稀疏化则是通过减少矩阵中的非零元素来降低矩阵的复杂性。如果说 SVD 是奔着矩阵的低秩近似去的，那么相应地寻找矩阵稀疏近似的算法又是什么呢？

接下来我们要学习的是论文《Monarch: Expressive Structured Matrices for Efficient and Accurate Training》[1]，它为上述问题给出了一个答案——“Monarch 矩阵”，这是一簇能够分解为若干置换矩阵与稀疏矩阵乘积的矩阵，同时具备计算高效且表达能力强的特点，论文还讨论了如何求一般矩阵的 Monarch 近似，以及利用 Monarch 矩阵参数化 LLM 来提高 LLM 速度等内容。

值得指出的是，该论文的作者也正是著名的 Flash Attention 的作者 Tri Dao，其工作几乎都在致力于改进 LLM 的性能，这篇 Monarch 也是他主页 [2] 上特意展示的几篇论文之一，单从这一点看就非常值得学习一番。

SVD回顾

首先我们来简单回顾一下 SVD（奇异值分解）。对于矩阵 大小的矩阵A，SVD 将它分解为

其中 分别是形状为 、 的正交矩阵， 则是 的对角矩阵，对角线元素非负且从大到小排列。当我们只保留 的前 r 个对角线元素时，就得到了 A 的一个秩不超过 r 的近似分解：

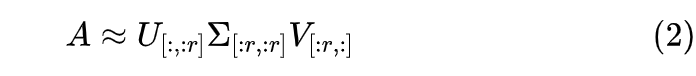
这里下标就按照 Python 的切片来执行，所以 的形状为 、 的形状为 以及 的形状为 ，这意味着 的秩至多为r。

特别地，由 SVD 得到的如上低秩近似，正好是如下优化问题的精确解：

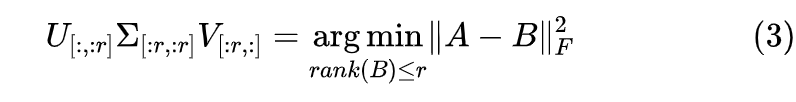
其中 是矩阵的 Frobenius 范数 [3] 的平方，即矩阵每个元素的平方和。也就是说，在 Frobenius 范数下，矩阵 A 的最优 r 秩近似就是 ，该结论被称为“Eckart-Young 定理 [4]”。也正是因为这个结论，我们在文章开头才说“SVD 是奔着矩阵的低秩近似去的”。

SVD 可以展开讨论的内容非常多，甚至写成一本书也不为过，这里就不再继续深入了。最后说一下，SVD 的计算复杂度是 ，因为我们至少要对 或 之一做特征值分解。如果我们确定做 SVD 是为了寻找r秩近似，那么复杂度可以有所降低，这便是 Truncated SVD。

Monarch矩阵

低秩分解应用非常广，但它未必总是符合我们的需求，比如可逆方阵的低秩近似必然不可逆，这意味着低秩近似不适合需要求逆的场景。此时另一个选择是稀疏近似，稀疏矩阵通常能够保证秩不退化。

注意稀疏和低秩并无必然联系，比如单位阵就是很稀疏的矩阵，但它可逆（满秩）。寻找矩阵的稀疏近似并不难，比如将绝对值最大的 k 个元素外的所有元素都置零就是一个很朴素的稀疏近似，但问题是它通常不实用，所以难在寻找实用的稀疏近似。所谓“实用”，指的是保留足够表达能力或近似程度的同时，实现一定程度的稀疏化，并且这种稀疏化具有适当的结构，有助于矩阵运算（比如乘法、求逆）的提速。

Monarch 矩阵正是为此而生，假设 是一个平方数，那么 Monarch 矩阵是全体 n 阶矩阵的一个子集，我们记为 ，它定义为如下形式的矩阵的集合：

其中P是 的置换矩阵（正交矩阵）， 是分块对角矩阵。下面我们来逐一介绍它们。

2.1 置换矩阵

置换矩阵P实现的效果是将向量 置换成新的向量

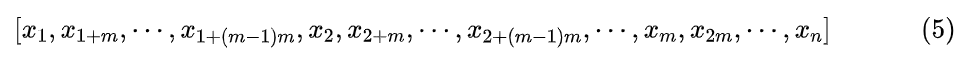
当然这样写大家可能依然觉得迷糊，然事实上用代码实现非常简单：

1Px = x.reshape(m, m).transpose().reshape(n)

如下图所示：

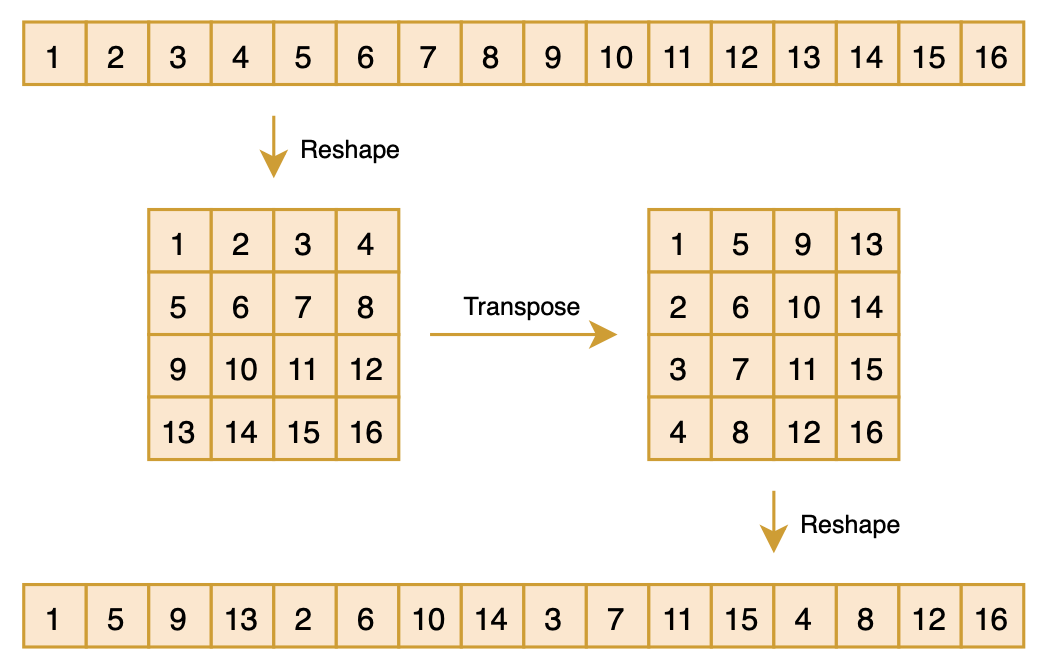▲ 转置矩阵P的示意图

之前做 CV 的读者可能会觉得这个操作有点熟悉，它其实就是 ShuffleNet [5] 中的“Shuffle”操作，这样对向量先 reshape 然后 transpose 最后再 reshape 回来的组合运算，起到一种“伪 Shuffle”的效果，它也可以视为 m 进制的“位反转排序”[6]。很明显，这样的操作做两次，所得向量将复原为原始向量，所以我们有 ，所以 。

2.2 分块对角

说完P，我们再来说 ，它们也是 大小的矩阵，不过它们还是 的分块对角矩阵，每个块是 大小，如下图所示：

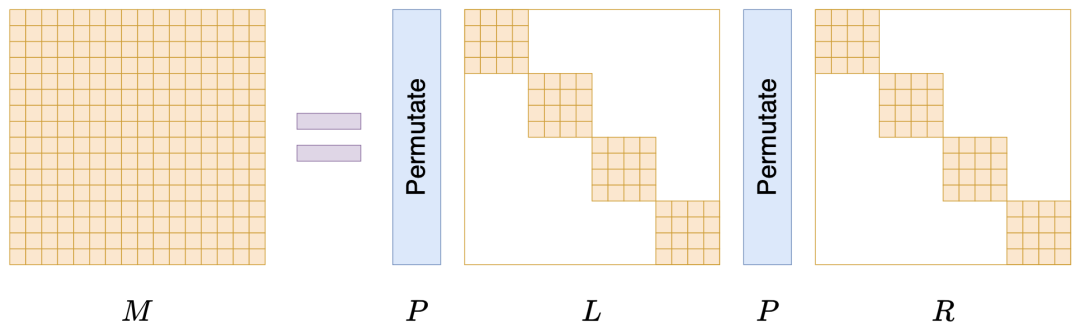
▲ Monarch矩阵形式M=PLPR

当 n 足够大时， 中零的数量占主导，所以 都是稀疏矩阵，即 Monarch 矩阵是具备稀疏特性的矩阵分解形式。由于 P 是固定的，所以 PLPR 中的可变元素就来源于 的非零元素，因此，矩阵 M 虽然是 的矩阵，但它实际自由参数不超过 个。从 1.5 这个数字我们就可以窥见 Monarch 矩阵的意图了，它希望将原本需要平方复杂度的运算，通过 Monarch 矩阵近似降低到 1.5 次方复杂度。

2.3 效率简析

那么 Monarch 矩阵能否达到这个目的呢？换句话说 Monarch 矩阵能否达到前面说的“实用”标准？表达能力方面我们后面再谈，我们先看计算高效方面。

比如“矩阵-向量”乘法，标准的复杂度是 ，但如果是Monarch矩阵的话我们有 ，由于乘P只是简单的reshape和transpose，所以它几乎不占计算量，主要计算量来源于L或R跟一个向量相乘。由于 的分块对角矩阵的特点，我们可以将向量为m组，继而转化为m个 的矩阵与m维向量相乘，总复杂度是 ，比 更低。

再比如求逆，我们考虑 ，n阶矩阵求逆的标准复杂度是 ，但对于Monarch矩阵我们有 ，主要计算量来源于 、 以及对应的“矩阵-向量”乘法，由于 都是分块对角阵，我们只需要分别对每个对角线上的块矩阵求逆，也就是共有 2m 个 的矩阵求逆，复杂度是 ，同样低于标准的 。要单独写出 也是可以的，但需要利用到后面的恒等式（8）。

所以结论就是，由于 P 乘法几乎不占计算量以及 是分块对角矩阵的特点，n 阶 Monarch 矩阵相关运算，基本上可以转化为 2m 个 矩阵的独立运算，从而降低总的计算复杂度。所以至少计算高效这一点，Monarch 矩阵是没有问题的，并且由于 的非零元素本身已经方形结构，实现上也很方便，可以充分利用 GPU 进行计算，不会带来不必要的浪费。

Monarch分解

确认 Monarch 矩阵的有效性后，接下来应用方面的一个关键问题就是：给定任意的 阶矩阵 A，如何求它的 Monarch 近似呢？跟 SVD 类似，我们定义如下优化问题

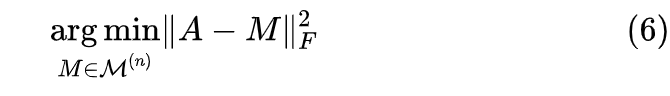
非常幸运的是，这个问题有一个复杂度不超过 的求解算法，这比 SVD 的 还要更高效一些。

3.1 高维数组

理解这个算法的关键一步，是将 Monarch 相关的矩阵、向量都转化为更高维数组的形式。具体来说，Monarch 矩阵 M 本来是一个二维数组，每个元素记为 ，表示该元素位于第 i 行、第 j 列，现在我们要按照分块矩阵的特点，将它等价地表示为四维数组，每个元素记为 ，表示第 i 大行、第 j 小行、第 k 大列、第 l 小列的元素，如下图所示：

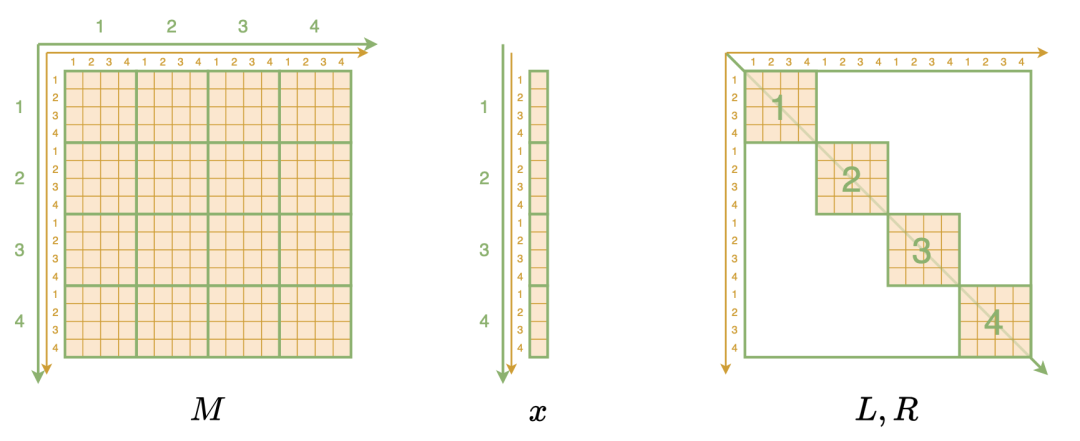
▲ 将Monarch相关矩阵/向量视为高维数组

虽然说起来挺费劲的，但事实上代码就一行：

1M.reshape(m, m, m, m)

同理，n 维（列）向量 x 也被转为 的二维数据，代码也是一行 x.reshape(m, m) 。剩下的 自然是表示为 的三维数组，如 表示第 i 块、第 j 小行、第 k 小列的元素，这本来也是 最高效的储存方式，但为了统一处理，我们也可以用 Kronecker delta 符号 [7] 将它们升到四维，比如 ã€�。

3.2 新恒等式

接下来，我们将推出 M 与 的一个新关系式。首先，可以证明在二维表示中，矩阵 P 与向量 x 的乘法变得更简单了，结果就是 x 的转置，即 ，所以我们有 ；接着，两个矩阵的乘法，在四维表示之下求和指标也有两个，所以

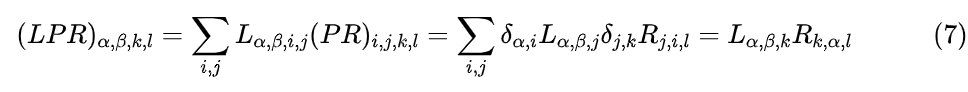
最后就是 ，将 换回 得到 ，又因为 M=PLPR，所以有

从这个等式可以看出，当我们固定一对 (j,k) 时，左边是一个子矩阵，右边是两个向量的外积，这意味着如果我们要给矩阵 A 找 Monarch 近似，只需要将 A 按照同样方式转为四维数组，并固定一对 (j,k)，那么问题就变成了找对应子矩阵的“秩-1近似”！

换句话说，有了这个恒等式之后，给矩阵 A 找 Monarch 近似可以转化为给 个子矩阵找“秩-1近似”，这可以用 SVD 完成，每个复杂度不超过 ，所以总复杂度不超过 。

3.3 参考实现

笔者简单用 Numpy 写的参考实现如下：

1import numpy as np
 2
 3def monarch_factorize(A):
 4    M = A.reshape(m, m, m, m).transpose(1, 2, 0, 3)
 5    U, S, V = np.linalg.svd(M)
 6    L = (U[:, :, :, 0] * S[:, :, :1]**0.5).transpose(0, 2, 1)
 7    R = (V[:, :, 0] * S[..., :1]**0.5).transpose(1, 0, 2)
 8    return L, R
 9
10def convert_3D_to_2D(LR):
11    X = np.zeros((m, m, m, m))
12    for i in range(m):
13        X[i, i] += LR[i]
14    return X.transpose(0, 2, 1, 3).reshape(n, n)
15
16m = 8
17n = m**2
18A = np.where(np.random.rand(n, n) > 0.8, np.random.randn(n, n), 0)
19
20L, R = monarch_factorize(A)
21L = convert_3D_to_2D(L)
22R = convert_3D_to_2D(R)
23PL = L.reshape(m, m, n).transpose(1, 0, 2).reshape(n, n)
24PR = R.reshape(m, m, n).transpose(1, 0, 2).reshape(n, n)
25
26U, S, V = np.linalg.svd(A)
27
28print('Monarch error:', np.square(A - PL.dot(PR)).mean())
29print('Low-Rank error:', np.square(A - (U[:, :m] * S[:m]).dot(V[:m])).mean())

笔者简单对比了一下 SVD 求出的秩-m 近似（此时低秩近似跟 Monarch 近似参数量相当），发现如果是完全稠密的矩阵，那么秩-m近似的平方误差往往优于 Monarch 近似（但不多），这也是意料之中，因为从 Monarch 近似的算法就可以看出它本质上也是个定制版的 SVD。不过，如果待逼近矩阵是稀疏矩阵时，那么 Monarch 近似的误差往往更优，并且越稀疏越优。

Monarch推广

到目前为止，我们约定所讨论的矩阵都是 n 阶方阵，并且 是一个平方数。如果说方阵这个条件尚能接受，那么 这个条件终究还是太多限制了，因此有必要至少将 Monarch 矩阵的概念推广到非平方数 n。

4.1 非平方阶

为此，我们先引入一些记号。假设 b 是 n 的一个因数， 表示全体 大小的分块对角矩阵，其中每个块大小是 的子矩阵，很明显它是前面 的一般化，按照这个记号我们可以写出。

此外，我们还要一般化置换矩阵 P，前面我们说了 P 的实现是 Px = x.reshape(m, m).transpose().reshape(n) ，现在我们一般化为 Px = x.reshape(n // b, b).transpose().reshape(n) ，记为 。

有了这些记号，我们可以定义一般的 Monarch 矩阵（原论文的附录）：

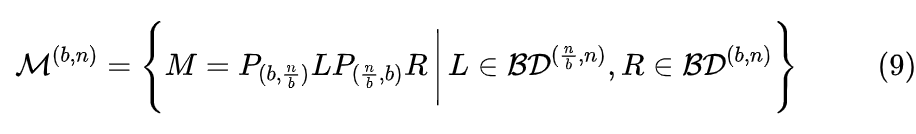
示意图如下：

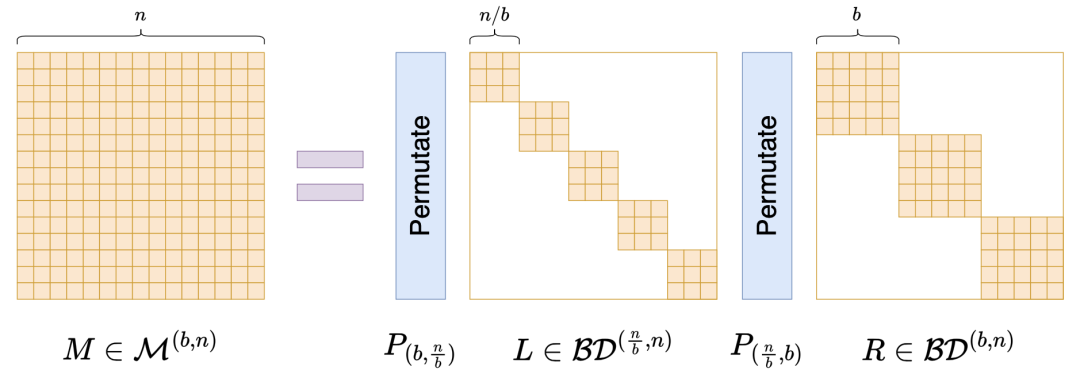
▲ 将Monarch矩阵推广到非平方阶方阵

前面所定义的 Monarch 矩阵，在这里可以简单记为 。不难计算，L 的非零元素至多有 个，R 的非零元素至多有 nb 个，加起来是 ，它在 取得最小值，所以 属于最稀疏的一个例子。

4.2 只要形式

可能读者会困惑，为什么要区分 , ，统一用一个不行吗？事实上，这样设计是为了保持高维表示下式（8）依然成立，从而可以推出类似的分解算法（请读者补充一下），以及可以从理论上保证它的表达能力。

如果我们不在意这些理论细节，只希望构造一个带有稀疏特性的矩阵参数化方式，那么就可以更灵活地对 Monarch 矩阵进行推广了，比如

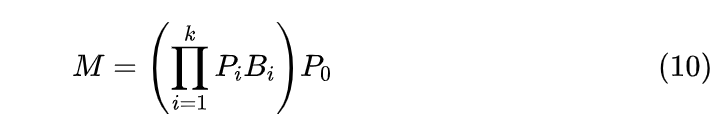
其中 ， 都是置换矩阵，最后多乘一个 是出于对称性的考虑，并不是必须的，如果你觉得有必要，还可以给每个 选择不同的 b，即 。

甚至，你可以结合低秩分解的形式，推广到非方阵的块矩阵，如下图：

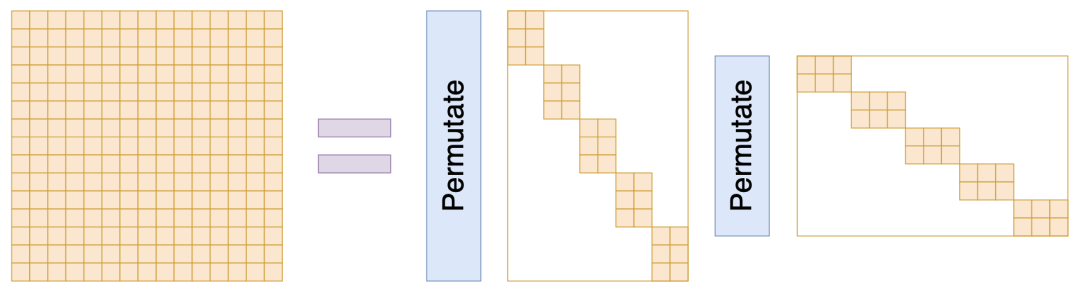
▲ 结合了低秩和稀疏的类Monarch矩阵参数化

基于这个类比，我们还可以进一步将 Monarch 矩阵的概念推广到非方阵。总之，如果只是需要一种类似 Monarch 矩阵的稀疏化结构矩阵，而不在意理论细节，那么结果就仅限于我们的想象力了。

应用例子

目前看来，Monarch 矩阵最大的特点就是对矩阵乘法比较友好，所以最大的用途无非就是替换全连接层的参数矩阵，从而提高全连接层的效率，这也是原论文实验部份的主要内容。

我们又可以将其分为“事前处理”和“事后处理”两类：“事前处理”就是在训练模型之前就将全连接层的参数矩阵改为 Monarch 矩阵，这样训练和推理都能提速，训练出来的模型也最贴合 Monarch 矩阵。

“事后处理”就是已经有一个训练好的模型，此时我们可以用 Monarch 分解给全连接层的参数矩阵找一个 Monarch 近似，然后替换掉原来的矩阵，必要时再简单微调一下，以此提高原始模型的微调效率或推理效率。

除了替换全连接层外，《Monarch Mixer: A Simple Sub-Quadratic GEMM-Based Architecture》[8] 还讨论了更极端的做法——作为一个Token-Mixer模块直接替换 Attention 层。

不过就笔者看来，Monarch-Mixer 并不算太优雅，因为它跟 MLP-Mixer [9] 一样，都是用一个可学的矩阵替换掉 Attention 矩阵，只不过在 Monarch-Mixer 这里换成了 Monarch 矩阵。这样的模式学到的是静态的注意力，个人对其普适性是存疑的。

最后，对如今的 LLM 来说，Monarch 矩阵还可以用来构建参数高效的微调方案（Parameter-Efficient Fine-Tuning，PEFT）。我们知道，LoRA 是从低秩分解出发设计的，既然低秩和稀疏是两条平行的路线，那么作为稀疏的代表作 Monarch 矩阵不应该也可以用来构建一种 PEFT 方案？

Google 了一下，还真有这样做的，论文名是《MoRe Fine-Tuning with 10x Fewer Parameters》[10]，还很新鲜，是 ICML 2024 的 Workshop 之一。

蝶之帝王

最后再简单说说 Monarch 矩阵的拟合能力。“Monarch”意为“帝王”、“君主”，取自“Monarch Butterfly（帝王蝴蝶）”一词，之所以这样命名，是因为它对标的是更早的“Butterfly 矩阵”[11]。

什么是 Butterfly 矩阵？这个说起来还真有点费劲。Butterfly 矩阵是一系列（ 个）Butterfly 因子矩阵的乘积，而 Butterfly 因子矩阵则是一个分块对角矩阵矩阵，其对角线上的矩阵叫做 Butterfly 因子（没有“矩阵”两个字），Butterfly 因子则是一个 的分块矩阵，它的每个块矩阵则是一个对角阵（套娃结束）。如下图所示：

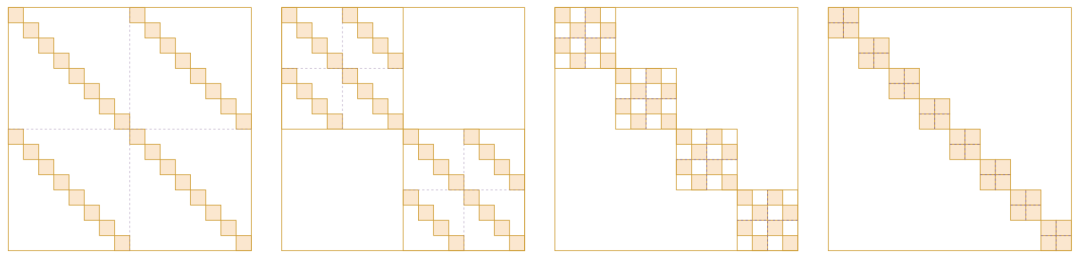
▲ Butterfly矩阵示意图

准确的 Butterfly 矩阵定义大家自行看论文就好，这里不详细展开。Butterfly 这个名字来源于作者觉得每个 Butterfly 因子的形状像 Butterfly（蝴蝶），当然像不像大家见仁见智，反正作者觉得像。从字面上来看，“Monarch Butterfly”比“Butterfly”更高级（毕竟是“帝王”），这暗示着 Monarch 矩阵比 Butterfly 矩阵更强。

确实如此，Monarch 论文附录证明了，不管 b 取什么， 都能覆盖所有的 n 阶 Butterfly 矩阵，并且 n > 512 时 严格大于全体 n 阶 Butterfly 矩阵集合，换言之 Butterfly 矩阵能做到的 Monarch 矩阵也能做到，反之未必。

我们也可以从“矩阵-向量”乘法复杂度来直观感知 Monarch 矩阵表达能力。我们知道，一个 矩阵乘以 n 维向量的标准复杂度是 ，但对于某些结构化矩阵可以更低，比如傅立叶变换可以做到 ，Butterfly 矩阵也是 ，Monarch 矩阵则是 ，所以 Monarch 矩阵“应该”是不弱于 Butterfly 矩阵的。

当然，Butterfly 矩阵也有它的好处，比如它的逆和行列式都比较好算，这对于 Flow 模型等需要求逆和行列式的场景更为方便。

文章小结

本文介绍了 Monarch 矩阵，这是 Tri Dao 前两年提出的一簇能够分解为转置矩阵与稀疏矩阵乘积的矩阵，具备计算高效的特点（众所周知，Tri Dao 是高性能的代名词），可以用来为全连接层提速、构建参数高效的微调方式等。

参考文献

[1] https://papers.cool/arxiv/2204.00595

[2] https://tridao.me/

[3] https://en.wikipedia.org/wiki/Matrix_norm#Frobenius_norm

[4] https://en.wikipedia.org/wiki/Low-rank_approximation

[5] https://papers.cool/arxiv/1707.01083

[6] https://en.wikipedia.org/wiki/Bit-reversal_permutation

[7] https://en.wikipedia.org/wiki/Kronecker_delta

[8] https://papers.cool/arxiv/2310.12109

[9] https://papers.cool/arxiv/2105.01601

[10] https://openreview.net/forum?id=AzTz27n6O2

[11] https://papers.cool/arxiv/1903.05895

更多阅读

#投 稿 通 道#

 让你的文字被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学术热点剖析、科研心得或竞赛经验讲解等。我们的目的只有一个，让知识真正流动起来。

📝 稿件基本要求：

• 文章确系个人原创作品，未曾在公开渠道发表，如为其他平台已发表或待发表的文章，请明确标注 

• 稿件建议以 markdown 格式撰写，文中配图以附件形式发送，要求图片清晰，无版权问题

• PaperWeekly 尊重原作者署名权，并将为每篇被采纳的原创首发稿件，提供业内具有竞争力稿酬，具体依据文章阅读量和文章质量阶梯制结算

📬 投稿通道：

• 投稿邮箱：hr@paperweekly.site 

• 来稿请备注即时联系方式（微信），以便我们在稿件选用的第一时间联系作者

• 您也可以直接添加小编微信（pwbot02）快速投稿，备注：姓名-投稿

△长按添加PaperWeekly小编

🔍

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

·

·

·