低秩近似之路（二）：奇异值分解（SVD）

PaperWeekly

于 2024-10-14 13:51:08 发布

阅读量594

点赞数 7

本文链接：https://blog.csdn.net/c9Yv2cf9I06K2A9E/article/details/142932775

版权

©PaperWeekly 原创 · 作者 | 苏剑林

单位 | 科学空间

研究方向 | NLP、神经网络

上一篇文章中我们介绍了“伪逆”，它关系到给定矩阵和（或）时优化目标的最优解。这篇文章我们来关注都不给出时的最优解，即

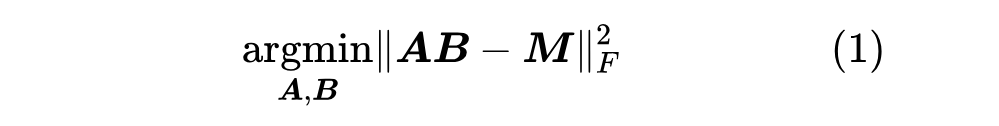
其中。说白了，这就是要寻找矩阵的“最优秩近似（秩不超过的最优近似）”。而要解决这个问题，就需要请出大名鼎鼎的 “SVD（奇异值分解）”了。虽然本系列把伪逆作为开篇，但它的“名声”远不如 SVD，听过甚至用过 SVD 但没听说过伪逆的应该大有人在，包括笔者也是先了解 SVD 后才看到伪逆。

接下来，我们将围绕着矩阵的最优低秩近似来展开介绍 SVD。

结论初探

对于任意矩阵，都可以找到如下形式的奇异值分解（SVD，Singular Value Decomposition）：

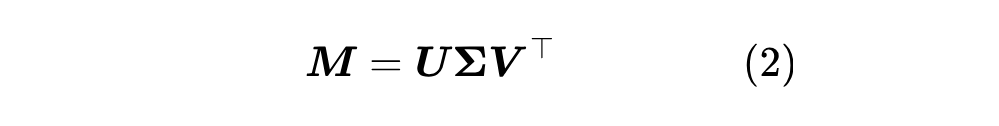
其中都是正交矩阵，是非负对角矩阵：

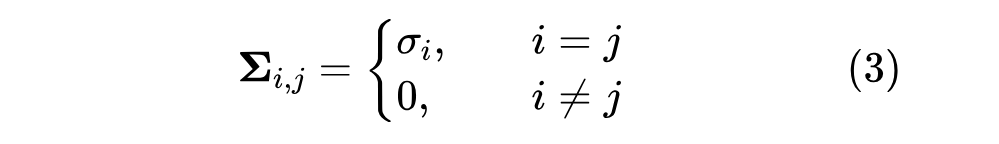
对角线元素默认从大到小排序，即，这些对角线元素就称为奇异值（Singular Value）。从数值计算角度看，我们可以只保留中非零元素，将的大小降低到（是的秩），保留完整的正交矩阵则更便于理论分析。

SVD 对于复矩阵同样成立，但需要将正交矩阵改为酉矩阵，转置改为共轭转置，但这里我们主要聚焦于跟机器学习关系更为密切的实矩阵结果。SVD 的基础理论包括存在性、计算方法以及它与最优低秩近似的联系等，这些内容笔者后面都会给出自己的理解。

在二维平面下，SVD 有非常直观的几何意义。二维的正交矩阵主要就是旋转（还有反射，但几何直观的话可以不那么严谨），所以意味着任何对（列）向量的线性变换，都可以分解为旋转、拉伸、旋转三个步骤，如下图所示：

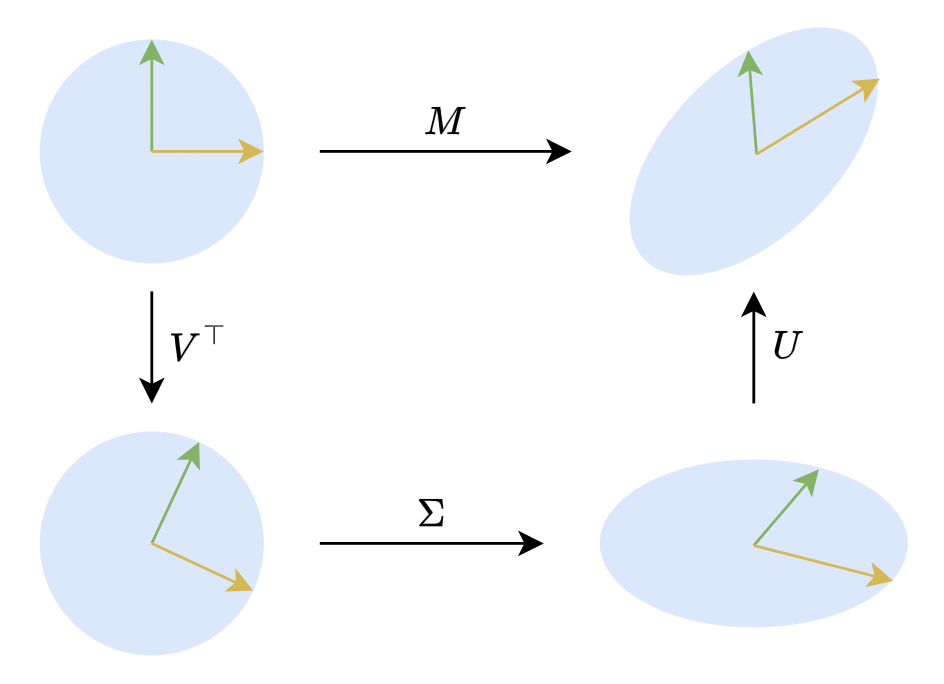
▲ SVD的几何意义

一些应用

不管是理论分析还是数值计算，SVD 都有非常广泛的应用，其背后的原理之一是常用的矩阵/向量范数对正交变换具有不变性，所以 SVD 左右两个正交矩阵夹着中间一个对角矩阵的特点，往往能用来将很多矩阵相关的优化目标转换为等价的非负对角矩阵特例，起到简化问题的作用。

伪逆通解

以伪逆为例，当的秩为时，我们有：

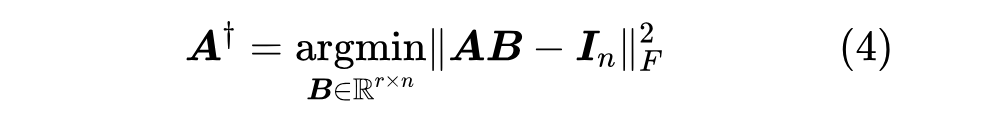
上一篇文章我们通过求导得出了的表达式，然后又花了一些心思推广到的秩小于的情形。但如果引入 SVD 的话，那么问题就简化得多了。我们可以将分解为，然后将表示成，注意我们没有规定是对角阵，所以总是可以做到的，于是：

最后一个等号是基于我们上一篇文章证明过的结论“正交变换不改变 F 范数”，这样我们就将问题简化成对角阵的伪逆了。接着我们可以用分块矩阵的形式将表示为：

这里的切片就按照 Python 数组的规则来理解。从最后的形式可以看出，要使得的范数最小，唯一解是，，说白了，就是将的非零元素都取倒数然后转置，我们将它记为，于是在 SVD 下就有：

可以进一步证明这个结果也适用于秩小于的，所以它是一个通用的形式，一些教程也直接将它作为伪逆的定义。此外，我们也可以观察到这个形式不区分左伪逆和右伪逆，这表明同一个矩阵的左伪逆和右伪逆是相等的，因此在说伪逆的时候不用特别区分左右。

矩阵范数

利用正交变换不改变 F 范数的结论，我们还可以得到

也就是说奇异值的平方和等于范数的平方。除了范数外，SVD 也可以用来计算“谱范数”。上一篇文章我们提到，范数只是矩阵范数的一种，另一种常用的矩阵范数是基于向量的范数诱导出来的谱范数，它定义为：

注意等号右端出现的范数都是向量的范数（模长，2- 范数），因此上述定义是明确的。由于它是向量的 2- 范数所诱导出来的，所以它也称为矩阵的 2- 范数。数值上，矩阵的谱范数等于它的最大奇异值，即。要证明这一点，只需要将做 SVD 为，然后代入谱范数的定义

第二个等号正是利用了正交矩阵不改变向量范数的特点。现在我们相当于将问题简化成为对角阵的谱范数，这个比较简单，设，那么

所以不超过，并且时取到等号，因此。对比范数的结果，我们还可以发现恒成立。

低秩近似

最后我们再回到本文的主题最优低秩近似，也就是目标（1）。将分解为，那么我们就可以写出：

注意仍可以代表任意秩不超过的矩阵，所以通过 SVD 我们将矩阵的最优秩近似简化成了非负对角阵的最优秩近似。

在《对齐全量微调！这是我看过最精彩的 LoRA 改进》中我们用同样思路求解过一个类似的优化问题：

利用 SVD 和正交变换不改变范数，可以得到

这就将原本一般矩阵的优化问题转化为是非负对角阵的特例，降低了分析难度。注意如果的秩不超过，那么的秩顶多为（假设 )），所以原始问题也是在求的最优秩近似，转化为非负对角阵后就是求非负对角阵的最优秩近似，跟前一个问题本质上是一样的。

理论基础

肯定了 SVD 的作用后，我们就需要补充一些理论证明了。首先要确保 SVD 的存在性，其次要找出至少一种计算方案，这样 SVD 的各种应用才算是切实可行的，接下来我们将用同一个过程把这两个问题一起解决掉。

谱之定理

在此之前，我们需要先引入一个“谱定理”，它既可以说是 SVD 的特例，也可以说是 SVD 的基础：

谱定理：对于任意实对称矩阵，都存在谱分解（也称特征值分解）

其中，是正交矩阵，是对角矩阵。

说白了，谱定理就是断言任何实对称矩阵都可以被正交矩阵对角化，这基于如下两点性质：

1. 实对称矩阵的特征值和特征向量都是实的；

2. 实对称矩阵不同特征值对应的特征向量是正交的。

这两点性质的证明其实很简单，这里就不展开了。基于这两点我们可以立马得出，如果实对称矩阵有个不同的特征值，那么谱定理成立：

其中是特征值，是对应的单位特征（列）向量，写成矩阵乘法形式就是，所以。证明的难点是如何拓展到有相等特征值的情形，但在思考完整的证明之前，我们可以先从一个不严谨的角度感受一下，这个不等特征值的结果是一定可以推广到一般情形的。

为什么这样说呢？从数值角度看，两个实数绝对相等的概率几乎为零，所以根本不需要考虑特征值相等的情形；用更数学的话说，那就是特征值不等的实矩阵在全体实矩阵中稠密，所以我们总可以找到一簇矩阵，当时它的特征值两两不等，当时它等于。这样一来，每个我们都可以分解为，取就得到的谱分解。

数学归纳

不幸的是，上面这段话只能作为一个直观但不严谨的理解方式，因为将这段话转化为严格的证明还是很困难的。事实上，严格证明谱定理的最简单方法可能是数学归纳法，即在任意阶实对称方阵都可以谱分解的假设上，我们证明也可以谱分解。

证明的关键思路是将分解为某个特征向量及其维正交子空间，从而可以应用归纳假设。具体来说，设是的一个非零特征值，是对应的单位特征向量，那么有，我们可以补充个跟正交的单位向量，使得成为一个正交矩阵。现在我们考虑：

注意到是一个阶方阵，并且很明显是一个实对称矩阵，所以根据假设它可以谱分解为，这里是阶正交矩阵，是阶对角阵，那么我们有。根据这个结果，我们考虑，可以验证它也是一个正交矩阵，并且

也就是说正是可以将对角化的正交矩阵，所以可以完成谱分解，这就完成了数学归纳法最关键的一步。

奇异分解

至此，所有准备工作都已经就绪，我们可以正式证明 SVD 的存在性，并给出一个实际计算的方案。

上一节我们引入了谱分解，不难发现它跟 SVD 的相似性，但也有两点明显区别：1）谱分解只适用于实对称矩阵，SVD 适用于任意实矩阵；2）SVD 的对角阵是非负的，但谱分解的则未必。那么，它们具体联系是什么呢？容易验证，如果的 SVD 为，那么：

注意到和都是对角阵，所以这意味着和的谱分解分别是和。这看起来将、分别做谱分解就可以得到的 SVD 了？确实没错，这可以作为 SVD 的一种计算方式，但我们无法直接通过它证明这样得出的满足。

解决问题的关键是只对或之一做谱分解，然后通过另外的方法构造另一侧的正交矩阵。

不失一般性，我们设的秩为，考虑对做谱分解为，注意是一个半正定矩阵，所以是非负的，并且假设对角线元素已经从大到小排列，秩意味着只有前个是大于 0 的，我们定义：

可以验证

这里约定切片的优先级高于转置、求逆等矩阵运算，即、等。上述结果表明是正交矩阵的一部份。接着我们有

注意是恒成立的，而是的前列，根据我们有可以写出，我们记，那么就有，由于秩的设定，所以当时，这意味着此时的实际上是一个零向量，所以

这表明，再结合是正交矩阵的一部分这一事实，我们已经得到了的 SVD 的关键部分，我们只需要将补零成大小的，将补全为的正交矩阵，那么就得到完整的 SVD 形式。

近似定理

最后，别忘了我们的最终目标是开始的优化问题（1）。有了 SVD 后，我们就可以给出答案了：

如果的 SVD 为，那么的最优秩近似为。

这称为 “Eckart-Young-Mirsky 定理”。在介绍 SVD 应用的“低秩近似”一节中，我们表明通过 SVD 可以将一般矩阵的最优 r 秩近似问题简化为非负对角阵的 r 秩近似，所以 “Eckart-Young-Mirsky 定理”相当于说非负对角阵的最优 r 秩近似就是只保留对角线最大的个元素的矩阵。

可能有读者认为“这难道不是显然成立吗？”，但事实是虽然结论很符合直觉，但它确实不是显然成立的。下面我们就聚焦于求解：