迷宫最短路径问题(ShortestPath)的求解——利用链式队列

迷宫最短路径问题(ShortestPath)的求解——利用链式队列

注：借助于栈求解迷宫问题时，并不能保证找到一条从迷宫入口到迷宫出口的最短路径。而借助于队列，可以找到从迷宫入口到迷宫出口的最短路径(如果有的话)。在迷宫中寻找最短路径问题在其他领域也存在，例如，在解决电路布线问题时，一种很常用的方法是在布线区域叠上一个网格，该网格把布线区域划分成n*m个方格，就像迷宫一样。从一个方格a的中心点连接到另一个方格b的中心点时，转弯处必须采取直角，如果已经有某条线路经过一个方格，则封锁该方格。希望使用a和b之间的最短路径来作为布线的路径，以便减少信号的延迟。

1. 迷宫问题的提法

• 迷宫问题是典型的图的搜索问题。
• 假设一个迷宫，只有一个入口和一个出口。如果从迷宫的入口到达出口，途中不出现行进方向错误，则得到一条最佳路线。
• 为此，用一个二维数组maze[m][n]来表示迷宫。
  (1)当数组元素maze[i][j]=1 (0≤i≤m-1,1≤j≤n-1)，表示该位置是墙壁，不能通行。
  (2)当数组元素maze[i][j]=0 (0≤i≤m-1,1≤j≤n-1)，表示该位置是通路，可以通行。
• 注：数组的第0行、第m-1行，第0列、第n-1列，必须是迷宫的围墙，即上述行列的所有坐标对应的数值必须为1(除了入口和出口两个位置的坐标对应的数值可以为0以外)，不能通行。

2. 利用队列求解最短路径的算法原理

• 先从位置a开始搜索，把从a可到达的相邻方格都标记为1(表示与a的距离为1)。
• 然后把从标记为1的方格可到达的相邻方格都标记为2(表示与a的距离为2)。
• 如此继续标记下去，直到到达位置b或者找不到可到达的相邻方格为止。
• 按照上述搜索过程，当最后到达b时，就可以在b上读出b与a之间的距离。
• 为了得到a和b之间的最短路径，从b开始，首先移动到一个比b的标号小的相邻位置上，一定存在这样的相邻位置，因为任一个方格上的标号与它相邻方格上的编号都相差1。
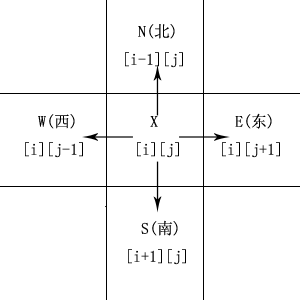
• 设任一时刻在迷宫中的位置[i][j]标记为X，X周围有4个前进方向，它实际是一系列交通路口，如果某一方向是0值，表示该方向有路可通，反之表示该方向已堵死。
• 为了有效地选择下一位置，可以将从位置[i][j]出发可能的前进方向预先定义在一个表内，按顺时针方向为Right([i][j+1])，Down([i+1][j])，Left([i][j-1])，Up([i-1][j])。
• (1)前进方向示意图：
  

• (2)前进方向表：

  Move[q].dir	move[q].a	move[q].b
  “N”	-1	0
  “E”	0	1
  “S”	1	0
  “W”	0	-1

3. 利用队列求解最短路径

3.1 链式队列的类定义及其操作的实现

• 文件：LinkedQueue.h

  
  #ifndef LINKED_QUEUE_H_
  
  
  #define LINKED_QUEUE_H_
  
  
  
  #include <iostream>
  
  
  using namespace std;
  
  template <class T>
  struct LinkNode         //链表结点类的定义
  {
      T data;             //数据域
      LinkNode<T> *link;  //指针域——后继指针
      //仅初始化指针成员的构造函数
      LinkNode(LinkNode<T>* ptr = NULL){ link = ptr; }
      //初始化数据与指针成员的构造函数
      LinkNode(const T& value, LinkNode<T>* ptr = NULL){ data = value; link = ptr; }
  };
  
  template <class T>
  class LinkedQueue
  {
  public:
      LinkedQueue();                      //构造函数
      ~LinkedQueue();                     //析构函数
  public:
      LinkNode<T>* getHead()