我们所说的微分中值定理,一般指三大微分中值定理。它包含
-
以米歇尔·罗尔的名字命名的--罗尔中值定理
-
以约瑟夫·路易·拉格朗日的名字命名的--拉格朗日中值定理
-
以及以奥古斯丁-路易·柯西的名字命名的--柯西中值定理

其中罗尔中值定理是基础,拉格朗日中值定理是罗尔中值定理的推广,柯西中值定理,是拉格朗日中值定理的推广。那么它们到底在讲什么呢?这节课,我们就来学习它们中的第一个,罗尔中值定理。
1 定义
定理(罗尔中值定理). 如果函数 满足:
那么 ,使得
。
若 是这样一个函数,在
内闭区间连续,开区间可导。则,在
区间内,至少存在一个导数为零的点。而我们知道,导数就是切线的斜率。斜率为零,意味着是水平的。那么存在一个导数为零的点,从几何上看,就是存在一个点,这个点的切线是水平的。

2 往返跑
对于折返跑,相信大家并不陌生,它的最大特点是,起点和终点在同一个位置。

下面,我们以时间为横坐标,位移为纵坐标建立坐标系。假设开始的时刻为 ,此时的位移为
。

当跑到最远位置的时候,位移最大,也就是函数值来到了最高点。
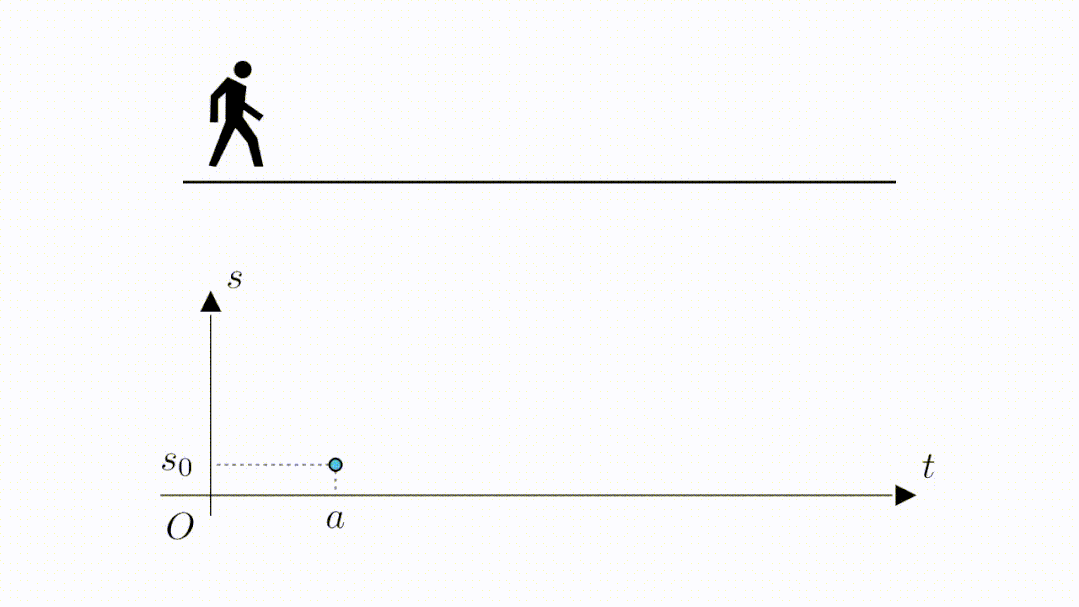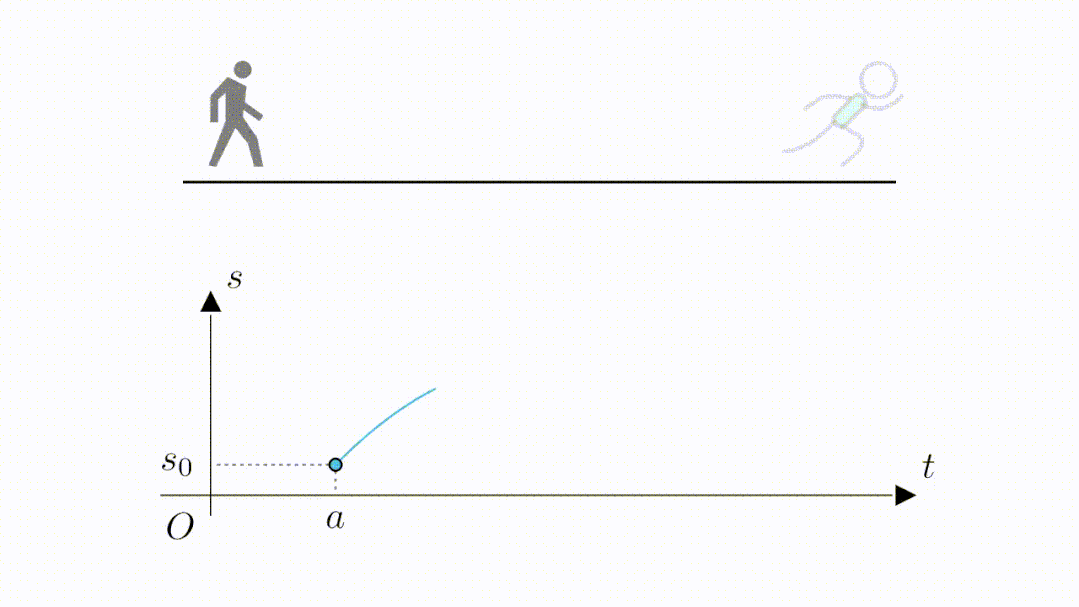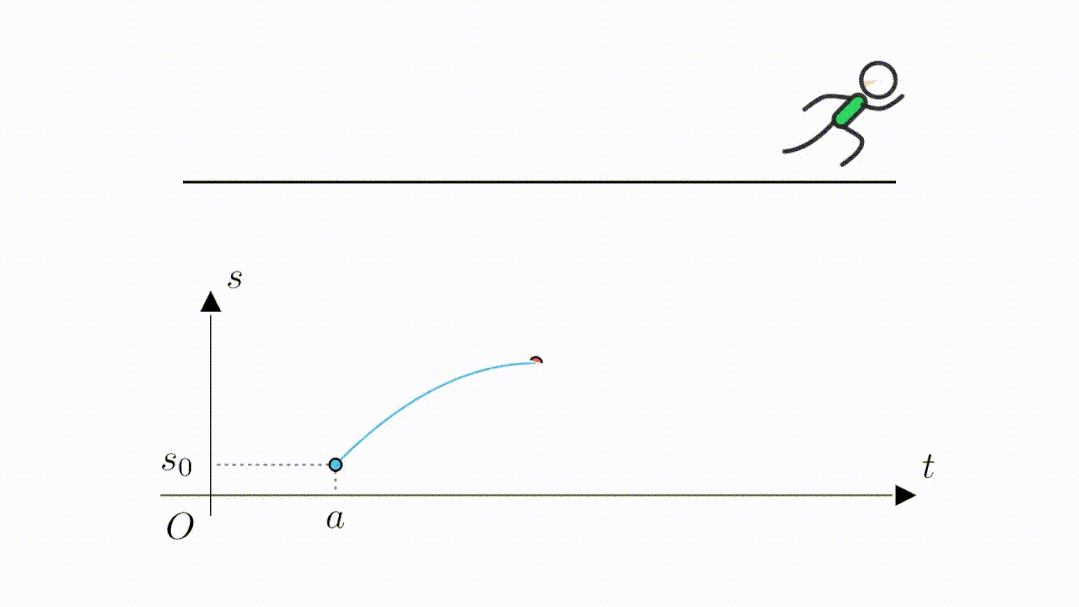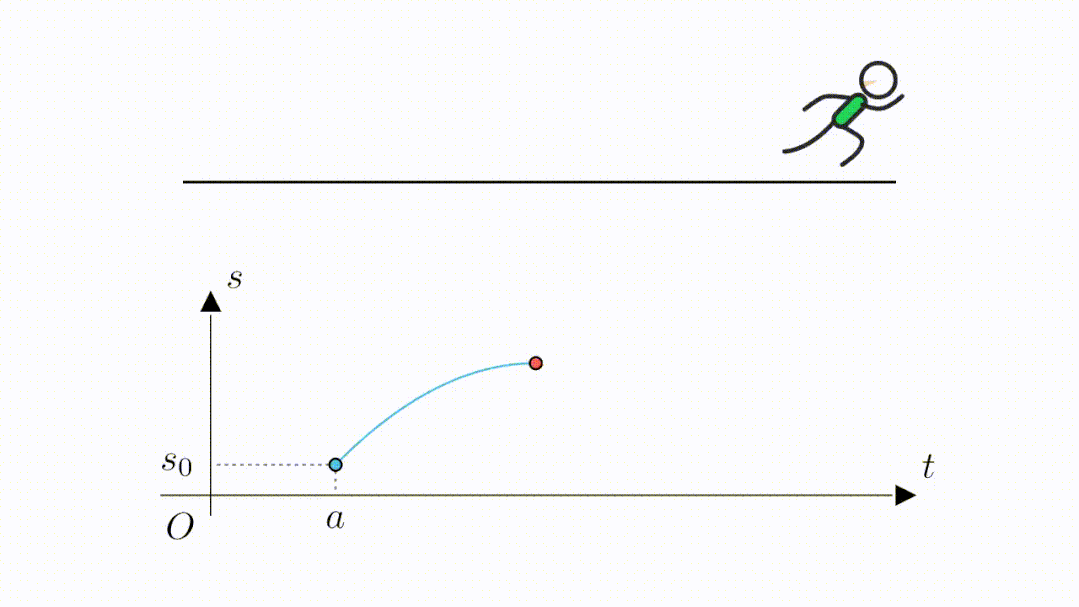
接着开始折返往回跑,函数值也就开始回落,当最后回到起点位置时,又来到了位移为 的位置。
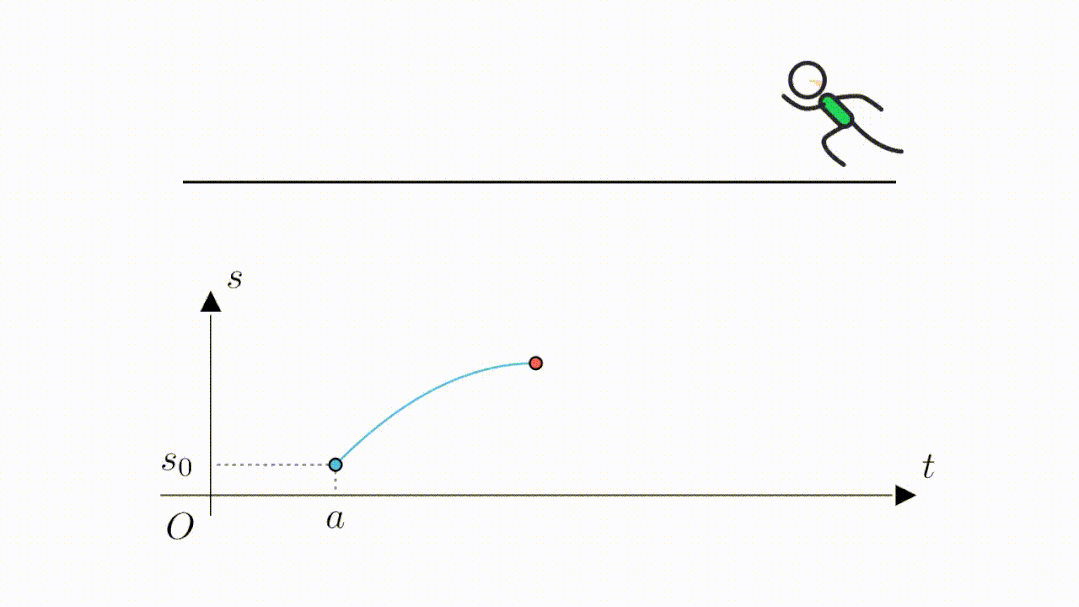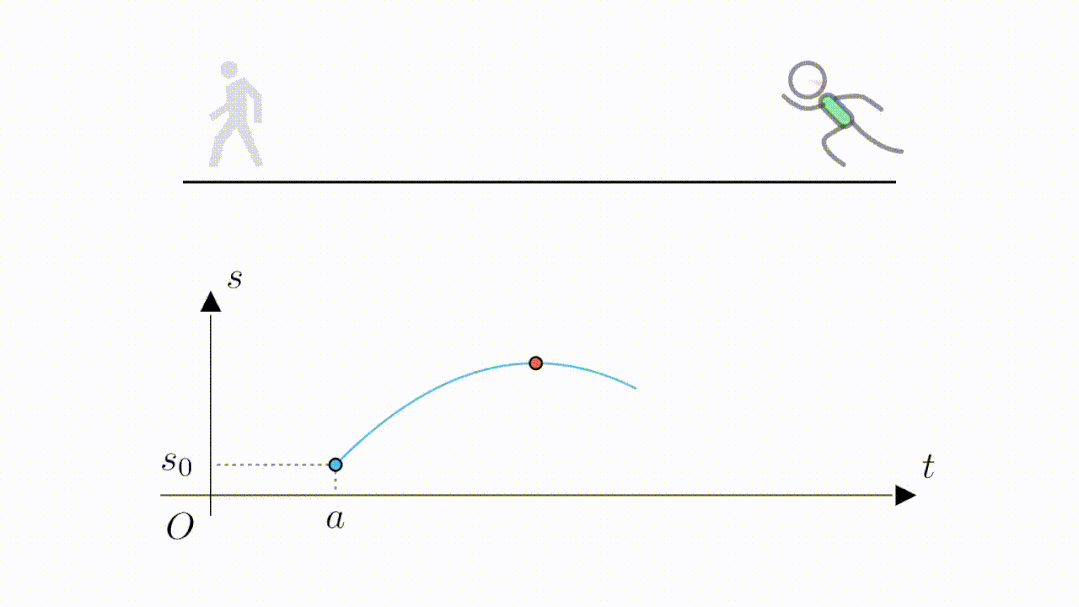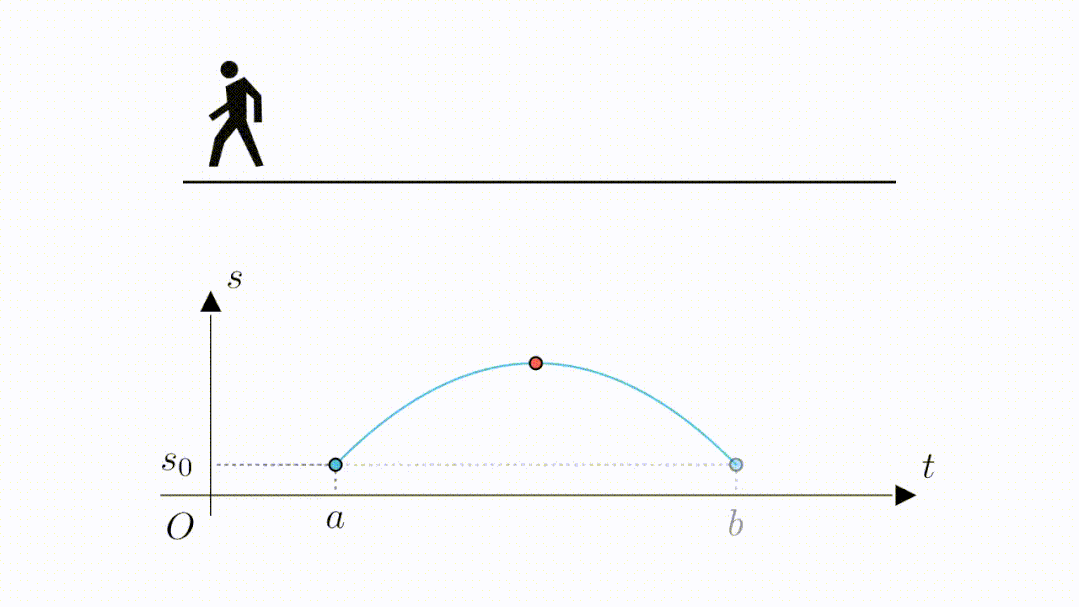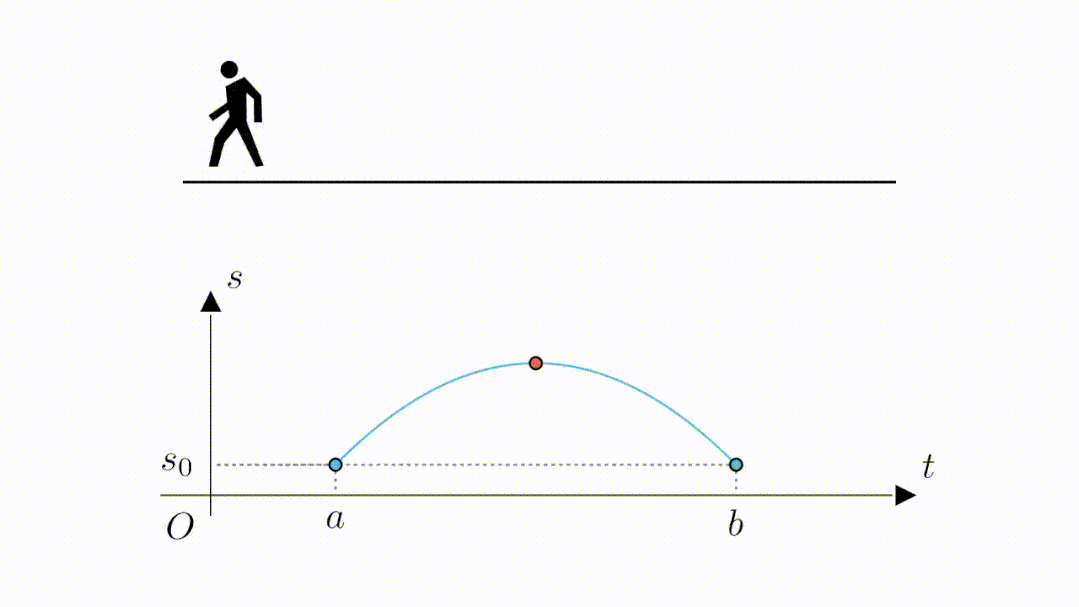
可以看到,此时这个时间位移函数,在 内,闭区间连续,开区间可导,且在起点时刻(
),与终点时刻(
),的函数值(
)是相同的,也就是说,这个时间位移函数,是符合罗尔中值定理的条件的。

那么按照定理的描述,就应该有个点导数为零,哪个点呢---最高这个点。

因为纵坐标为位移,那么最高这个点,其实就是距离起点最远的这个位置,此时折返跑要完成转向,因此必然出现一个速度为零的时刻。
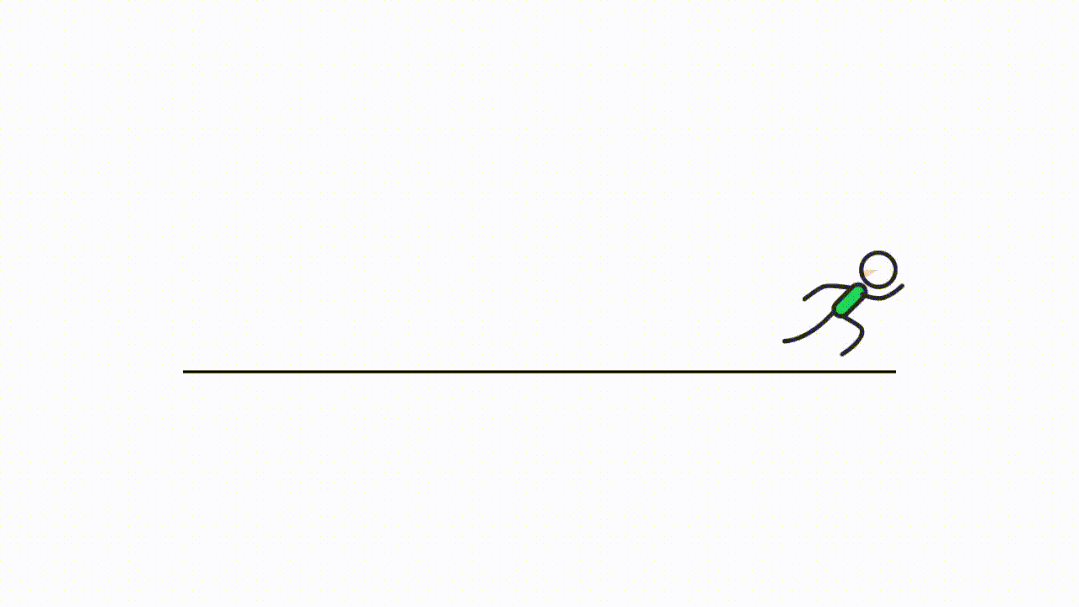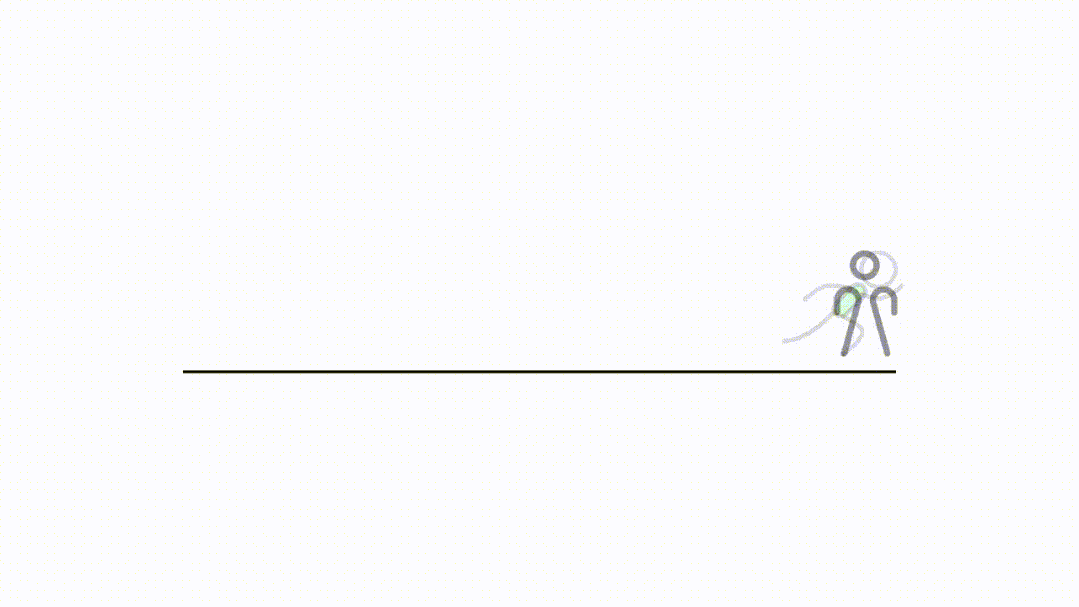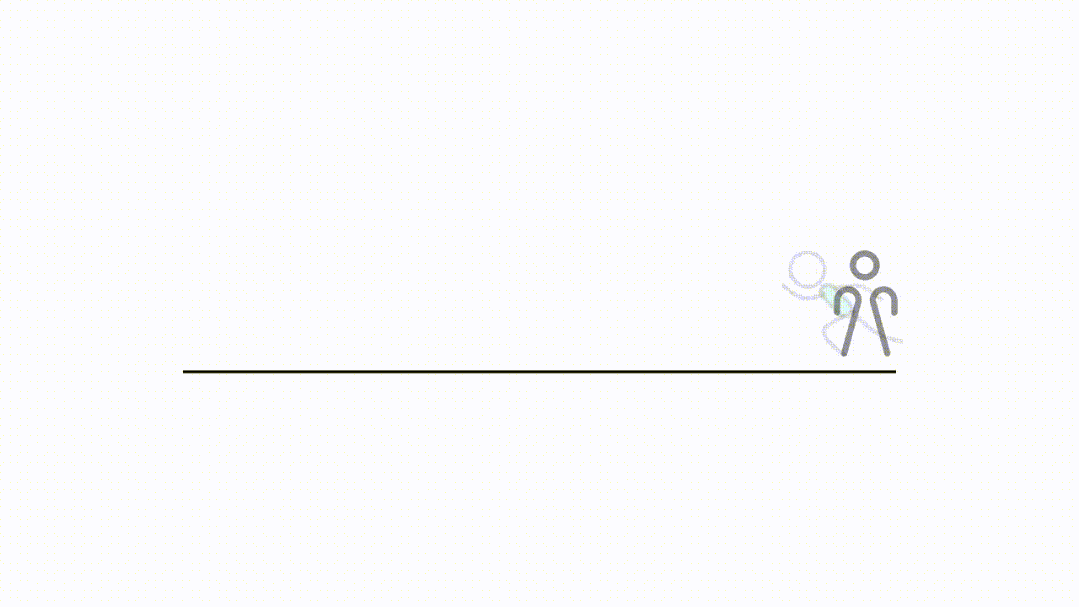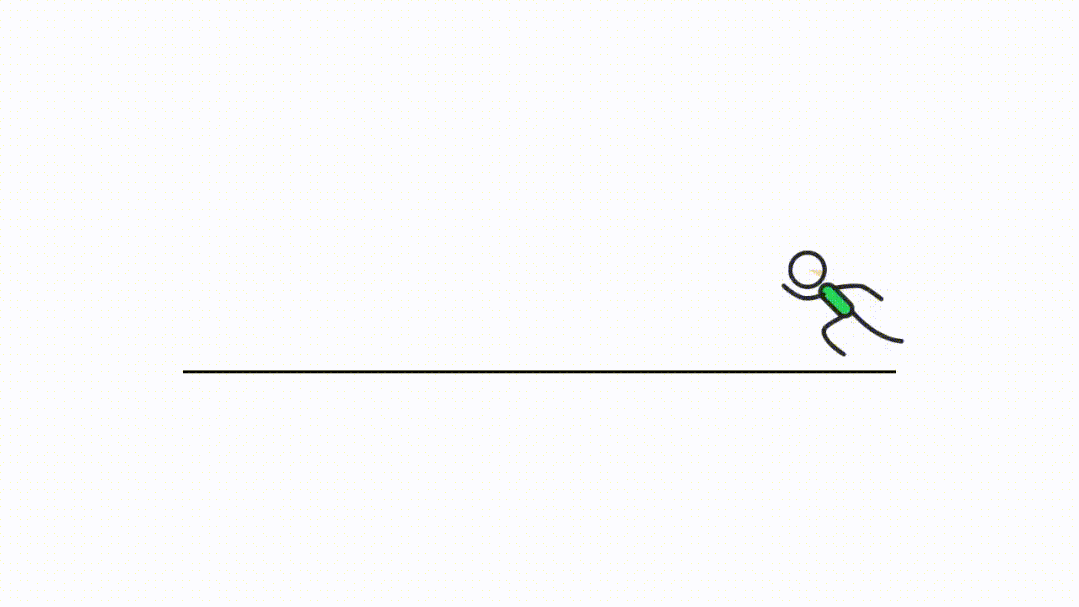
而我们知道,瞬时速度就是位移相对于时间的导数,假设我们在 这个时间点,速度为零,那么过
点的切线就是水平的

3 细节
3.1 至少一个点导数为零
罗尔中值定理中说的是,导数为零的点至少有一个,隐含意思是,导数为零的点可能有多个。

3.2 开区间可导
不少同学会疑惑,能不能将罗尔中值定理的条件进行如下修改?
答案是不可以,因为这样的修改并不等价,比如:

上述函数 就刚好满足“在闭区间
上连续,在开区间
上可导”,其在端点
和
处不可导,它也是可以运用罗尔中值定理的,即
使得
(甚至还有无穷多个):


























 5239
5239

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










