o1方法的推理能力无上限？LeCun怒怼：两层网络还可以万能近似呢

来源：AI科技前沿

OpenAI的o1大模型一经亮相，AI界便热议如何复制其成果。OpenAI对技术细节严格保密，试图从AI中获取完整推理过程，稍有过问即遭警告。技术报告中也难以寻觅线索。

于是，研究者们转向先前类似研究，试图挖掘线索。例如，Google Brain推理团队创始人Denny Zhou在5月发布的论文《Chain of Thought Empowers Transformers to Solve Inherently Serial Problems》，作者阵容强大，包括Denny Zhou、斯隆奖得主马腾宇及他的两位学生。

链接：https://arxiv.org/abs/2402.12875        

Denny Zhou宣称，通过让Transformer生成充足的中间推理tokens，已证明其能解决所有问题，并赋予LLM推理无限潜能。论文核心在于展示思维链（CoT）极大增强了Transformer的表述能力，使其能应对更复杂问题。

加入 CoT

单层的 Transformer 也能做复杂推理题

长久以来，寻求Transformer架构突破的努力不断。尽管Transformer擅长并行处理，但在串行推理上存在局限。论文作者提出CoT可助Transformer实现串行计算。他们运用电路复杂性来探讨Transformer的能力，电路复杂性按难度分为多个层级，如：

·AC⁰：仅含AND、OR、NOT门，层次有限，常用于解决基础并行计算问题。

·TC⁰：在AC⁰基础上，引入多数决定门，提升并行计算复杂性处理能力。

先前研究证实，纯解码器结构的 Transformer 可高效并行计算，但其计算局限，仅能处理 TC⁰级电路问题。在更严格的限制下，不使用多数决策门，Transformer 的计算能力仅限于 AC⁰级问题。         
         
研究发现，无CoT时，Transformer的串行计算次数受限于模型深度，深度越高，处理串行计算步数越多，但深度固定，无法随任务扩展。引入CoT后，问题得以解决，使Transformer能生成T步中间步骤，提升串行计算次数至T。   

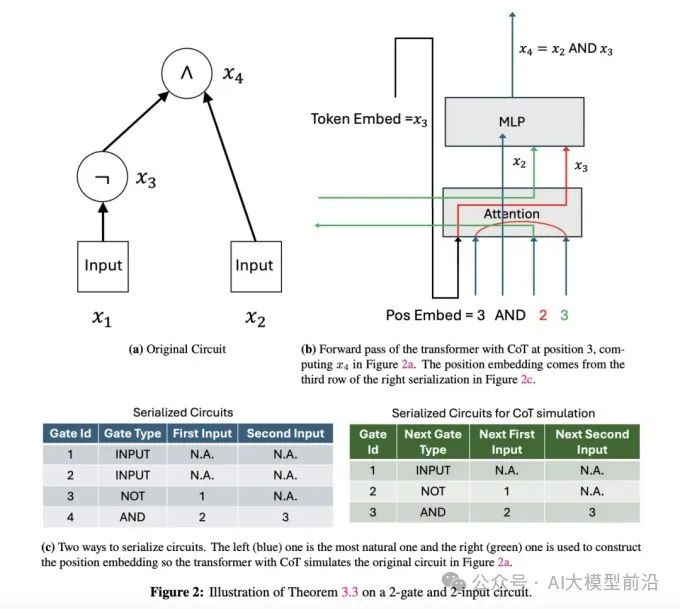
研究进一步证实，当Transformer的嵌入维度与输入序列长度的对数成正比，并采用T步中间层时，该模型可模拟T位布尔电路，进而攻克P/poly类难题。若T线性增加，Transformer便

能应对所有正则语言问题，乃至S₅等复杂群组合问题。为验证理论，作者通过实验对比了引入CoT前后，Transformer在处理模加法、排列组合、迭代平方及电路值四个关键任务上的成效，实验在三种不同配置中进行。

·Base模式：模型直接输出预测，核心是缩小预测值与实际值之间的误差。

·CoT 模式：针对每问题，手动构建思维链，检验模型对思维链中各 token 的预测准确性。

·提示模式：向模型输入部分提示，以优化其生成过程。对Base和Hint模式，均直接评定最终答案的正确性。

模加法（Modular Addition）：         
给定正整数 p，目标是用模运算求词表和。序列 x 由 {0, 1, ..., p-1} 采样生成，xₙ设为 '='。引入 CoT 后，浅层 Transformer 在短序列表现佳，长序列则更优。         
         
排列组合（Permutation Composition）：         给定 p，对 {1, ..., p, (,), =} 排列组合，输出整合结果。CoT 下，Transformer 部分计算结果。                   

迭代平方（Iterated Squaring）：         密码学中用于加密算法，计算难度高。Transformer 计算 rⁿ mod p，CoT 下准确率稳定。          

         
电路值问题（Circuit Value Problem）：         
计算电路值，序列长度短时准确，长序列用 CoT 可达高准确率。         
         
CoT 显著增强 Transformer，引发对 AGI 距离的思考。论文争议多，涉及幻觉问题、意义推理、实时学习限制等。模拟门电路等实验需在真实环境中验证，计算资源需求大。对 AGI 的实现路径，业界存在不同看法。   

CoT虽强大，但仅靠其扩展并非万能。论文提出一种构建Transformer权重的通用理论，有望提升特定任务适应度。尽管模型深度固定，CoT长度可长，但其权重能否通过梯度下降有效学习，尚待验证。

          
相较之下，人类推理简明高效，即便面对未知问题，也能迅速找到解决核心。田渊栋认为，探究如何构建这种表示，是一大迷人课题。他用生动比喻阐述此观点：仿佛「两层神经网络理论上可拟合所有数据，我们便盲目应用于各类场景」。

         
Yann LeCun 见状学生评论，亦发声支持：「我正想谈论此事，渊栋已抢先一步。」          
作为“深度学习三巨头”之一，LeCun 表示：「两层网络及核机器可无限逼近任何函数，故无需深度学习。从1995至2020，我多次听闻此论点！」   

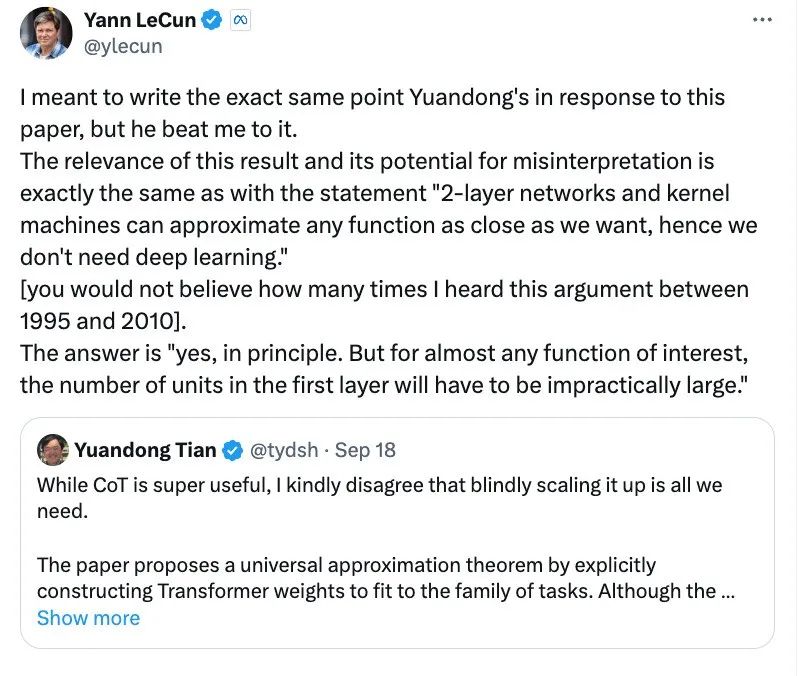     他进一步阐释：「理论可行，但实际应用中，两层网络可能导致第一层神经元数量过多，难以操作。」          

针对“两层MLP”比喻问题，生物学领域AI研究实验室EvolutionaryScale联合创始人Zeming Lin提出观点：     

   
「我认为需为机器学习模型构建类似乔姆斯基层次结构的框架，如NP、P、O(n^2)等概念，明确Transformer或Mamba的层次定位。」       

   
田渊栋赞同：「涉及数据分布、模型架构、学习算法、后处理等多方面，问题复杂度远超预期。」          

尽管田渊栋可能不完全同意论文思路，但仍认可持续尝试的必要性。       

 
而这篇关于CoT提升基于Transformer架构LLM推理能力的论文，却让一向对AGI持保留态度、多次质疑LLM无法实现AGI的LeCun面临更尖锐的挑战：

我犹记你言，LLM（GPT）非AI，且难至AGI，因其缺乏推理能力。

然而，凭借CoT+RL，它如今已具备推理能力。该论文仅确认了先前工作的正确性，继续保持着一贯的准确性。

Meta 对通往 AGI 的主流途径持保留态度，这并非仅因个人情感。     

   

或许正如网友所言，“似乎有人已掌握拓展CoT的方法，OpenAI对此信心满满。”而对于争论的核心——CoT能否使Transformer解决一切问题，还需更多研究来证实。

未来知识库是“欧米伽未来研究所”建立的在线知识库平台，收藏的资料范围包括人工智能、脑科学、互联网、超级智能，数智大脑、能源、军事、经济、人类风险等等领域的前沿进展与未来趋势。目前拥有超过8000篇重要资料。每周更新不少于100篇世界范围最新研究资料。欢迎扫描二维码或点击本文左下角“阅读原文”进入。