AK F.*ing leetcode 流浪计划之费马小定理与组合数取模

欢迎关注更多精彩
关注我，学习常用算法与数据结构，一题多解，降维打击。

费马小定理与证明

参考 https://zhuanlan.zhihu.com/p/594859227

费马小定理：如果p是一个质数，而正整数a不是p的倍数，那么a^(p-1)≡1（mod p）。

证明：

引理1 S={1a, 2a, 3a, …, (p-1)a}，S里所有数都不是p的倍数

由于 1到p-1都小于p, a也不能被p整除，说明a, 1到p-1 这些数都没有因子p。

由此引理1得证明。

引理2 S中所有元素对p取模不为0，且正好为集合 N = {1,2,3,…, p-1}

由引理1可知，对于任意小于p的两个不相同整数, i, j, ia%p != ja%p !=0。

假设 ia%p = ja%p，则 i%p * a%p = j%p * a%p, 得出i=j，与条件矛盾。

所以，对于S%p所有数字不相同，总个数为p-1个，由鸽巢原理可知，引理2正确。

根据引理2，可得到 $\prod _S\%p=\prod _N\%p$

两边整理得到 $a^{p-1}(p-1)!\%p=(p-1)!\%p$

由于gcd(p, (p-1)!)=1, 得到 a^(p-1)%p=1。

逆元

定义

已知整数a,p , a与p互质，如果存在一个数c<p使得 a*c%p=1, 则称c为a在模p下的逆元，记c=a^-1 %p;
通俗理解就是求(1/a)%p。

用费马小定理求逆元

a^(p-1)≡1（mod p）

可知 a*a^(p-2)%p=1

从定义可知 a在模p下的逆元为 a^(p-2)%p, 一般p是比较大的质数，可以使用快速幂求解。

typedef long long lld;
 
lld MOD = 998244353;
 
const int N = 1e6 + 10;
 // a的逆元为 fastmi(a, p-2)
lld fastmi(lld a, lld n) {
	lld ans = 1;
 
	while (n) {
		if (n & 1)ans = ans*a%MOD;
		
		a *= a;
		a %= MOD;
		n >>= 1;
	}
 
	return ans;
}

组合数取模

已经知p是一个比较大的质数（超过10的7次），求组合数C(n, m) , 0<=m<=n。

打表法

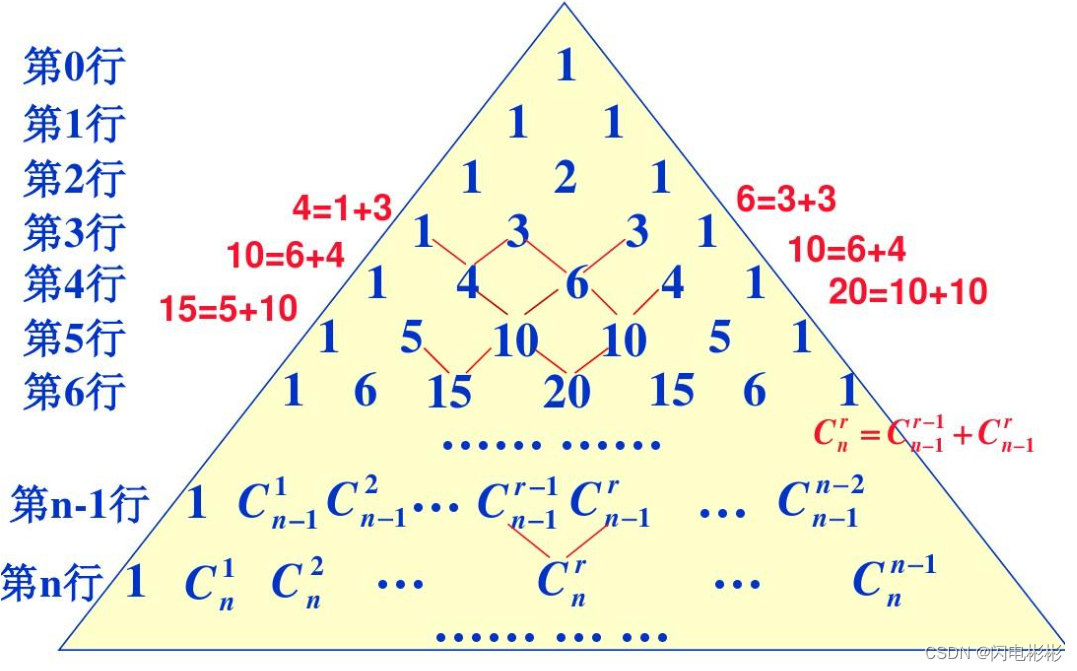
当n<=1000时，可以使用扬辉三角打表法。
用一个下三角矩阵存储组合数结果。
利用公式C[i][j] =( C[i - 1][j-1] + C[i - 1][j])%p，求解;

lld C[1010][1010];
 
void initC() {
	C[0][0] = 1;
	C[1][0] = C[1][1] = 1;
 
	for (int i = 2; i < 1010; i++) {
		C[i][0] = C[i][i] = 1;
		for (int j = 1; j < i; ++j) C[i][j] =( C[i - 1][j-1] + C[i - 1][j])%MOD;
	}
}

逆元法

$C_n^m=\frac{A_n^m}{m!}=\frac{n!}{m!(n-m)!}$

从上式可以看出当m不是很大时，m!的逆元是可以在O(n)log§时间内求出来的。

当n不大时也可以直接迭代得到n!%p。

如果n-m不大也可以直接求得 $A_n^m$

lld inv[N];
// 计算n! 的逆元, inv[n]=(1/n!)%p = (n!)^(p-2)%p
void initInv() {
	lld sum = 1;
	inv[0] = 1;
	for (lld i = 1; i < N; ++i) {
		sum *= i;
		sum %= MOD;
		inv[i] = fastmi(sum, MOD - 2);
	}
}

// 计算C(n, m) = n!/(n-m)!%p * inv[m]%p
lld C(lld n, lld m) {
	lld sum = 1;
	for (int i = n; i > (n - m); --i) sum = sum * i % MOD;
	return sum * inv[m] % MOD;
}

题目一

https://codeforces.com/contest/1967/problem/C

题目大意

题目基础相关知识：树状数组

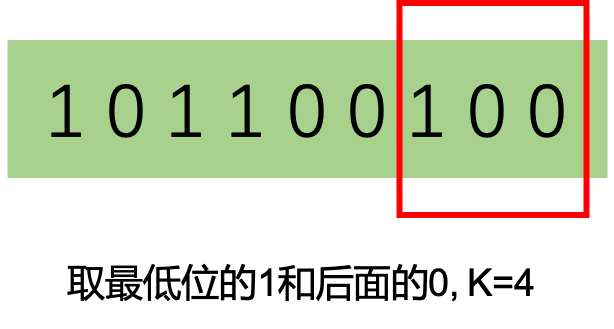
定义lowbit(x) 是由x二进制最低位的1和后面的0组成的数字，例如，lowbit(12)=4, lowbit(8)=8.

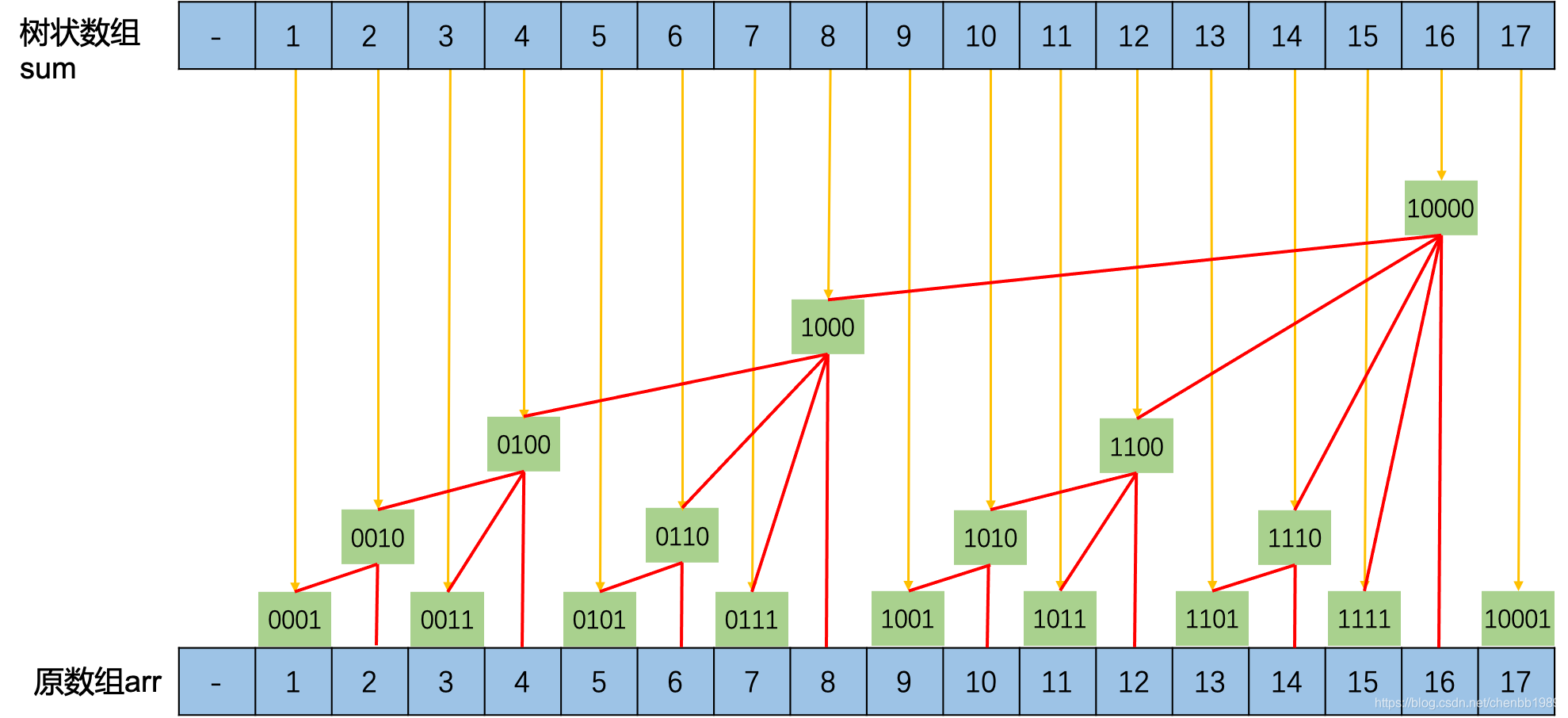
arr是一个长度为n数组。

假如一个长度为n的数组sum 满足 $su{m}_i=\left\{\sum _{j=i-lowbit(i)+1}^{i}arr[j]\right\}mod998244353$，则称sum为arr的二叉索引树。定义sum=f(arr)。

下图可以解释上述定义，红线为累加给上级关系。

给定一个数组a, 整数k，

$f^k(a)=\{\begin{array}{l}f(a)k=1\\ f(f^{k-1}(a))k>1\end{array}$

问题：给定结果sum,k 求最初始的数组arr。
n 为arr长度, 1≤n≤2⋅10⁵,1≤k≤10⁹

问题解析

既然是累加关系，那么可以尝试找到累加系数关系。之后就可以使用高斯消元法求解每个未知数。

设c[i]为sumi的累加系数。

$su{m}_i=\left\{\sum _{j=i-lowbit(i)+1}^{i}arr[j]\ast c[i][j]\right\}mod998244353$

假设已经知道系数，我们可以从低到高枚举i, 然后把用sumi把相关联的上级减掉，剩下的sum数组就是答案。

下面来寻找系数与k的关系

手动模拟一下：

假设现在数组长度为8。
当k=1时，
系数c如下

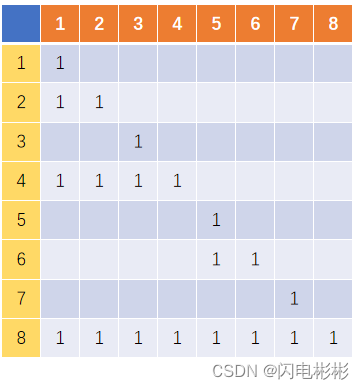
横坐标为arr[i], 纵坐标为sum[i]。

k=2, 在上面基础上再模拟一遍

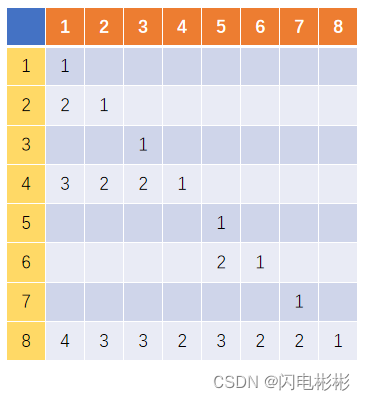
k=3，在上面基础上再模拟一遍

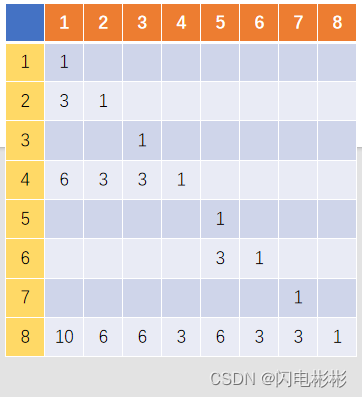
上面我们只看1，2，4，8行（从树上看是连续上级关系），

从上表观察发现每次K增加1，相应系数就是把k-1对应的系数全部加起来。
例如k=3时，c[8]1 = (c[8][1] + c[4][1]+c[2][1]+c[1][1])(k=2)

经过简单的分析可以得到以下一个表。

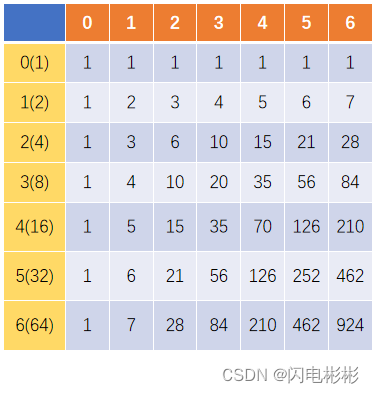
将上表命名为mat, 横坐标为k-1, 纵坐标为当前数字与目标数字的层数相。
可以看出下行就是上一行的前缀和。

至此，我们已经找到了k与系数的关系，但是k太大了，直接计算或者打表都不可能。

对上表进行旋转，可以得到扬辉三角，

也就是说mat[i][j] 与组合数C(n, m)存在一个关系。
通过线性变换可以得到 mat[i][j] = C(i+j, i)

实现细节

根据上面的推导

• sum[1] = arr[1];
• sum[2] = c[1][1]*arr[1] + arr[2];
• sum[3] = arr[3];
• sum[4] = c[4][1]*arr[1] + c[4][2]*arr[2] + c[4][3]*arr[3] + arr[4];
• sum[5] = arr[5];
• sum[6] = c[6][5]*arr[5] + arr[6];
• sum[7] = arr[7];
• sum[8] = c[8][1]*arr[1] + c[8][2]*arr[2] + c[8][3]*arr[3] +c[8][4]*arr[4] + c[8][5]*arr[5] + c[8][6]*arr[6] + c[8][7]*arr[7] + arr[8];
• …

d = dep[i]-dep[j], 在二叉树上的深度
$c[i][j]=mat[d][k-1]=C(d+k-1,d)=inv[d]\ast A_{d+k-1}^d$

可从i=1开始 用c[][]*sum[i] 去减掉所有上级树上加成项。
相当于d每次会加1，
$mat[d+1][k-1]=C(d+1+k-1,d+1)=inv[d+1]\ast A_{d+1+k-1}^{d+1}$
inv已经求好了。

$A_{d+1+k-1}^{d+1}=A_{d+k-1}^d\ast (d+1+k-1)$
根据上述递推式，可以一边递推一边减掉加成项。
这样可以平均O(1)求出系数c.

代码

#include <iostream>
#include <stdio.h>
#include <queue>
#include <string.h>
#include <stack>
#include <vector>
#include <map>
#include <algorithm>
#include <cmath>

using namespace std;

typedef long long lld;

lld MOD = 998244353;

const int N = 1e6 + 10;

lld fastmi(lld a, lld n) {
	lld ans = 1;

	while (n) {
		if (n & 1)ans = ans * a % MOD;

		a *= a;
		a %= MOD;
		n >>= 1;
	}

	return ans;
}

lld inv[N];

void initInv() {
	lld sum = 1;
	inv[0] = 1;
	for (lld i = 1; i < N; ++i) {
		sum *= i;
		sum %= MOD;
		inv[i] = fastmi(sum, MOD - 2);
		// if (i < 10)cout <<sum<<", "<< inv[i] << ", " << (inv[i]*sum%MOD) << endl;
	}
}

int lowbit(int x) {
	return x & (-x);
}

lld arr[N];

lld C[1010][1010];

void initC() {
	C[0][0] = 1;
	C[1][0] = C[1][1] = 1;

	for (int i = 2; i < 1010; i++) {
		C[i][0] = C[i][i] = 1;
		for (int j = 1; j < i; ++j) C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % MOD;
	}
}



void solve() {
	initInv();
	initC();
	int t;
	cin >> t;
	while (t--) {
		lld n, k;
		cin >> n >> k;
		for (int i = 1; i <= n; ++i)cin >> arr[i];

		for (int i = 1; i <= n; ++i) {
			lld isum = 1;
			for (int j = i + lowbit(i), d = 1; j <= n; j += lowbit(j), d++) {
				isum = isum * ((k - 1 + d) % MOD) % MOD;
				//cout << j<<", "<< d<<", "<< isum * inv[d] % MOD<<endl;
				arr[j] -= isum * arr[i] % MOD * inv[d] % MOD;
				arr[j] %= MOD;
				//cout << "mat" << k - 1 << ", " << d << endl;
				//cout << "C" << k - 1 +d<< ", " << d<< "=" << isum * inv[d] % MOD<< endl;
				/*arr[j] -= C[k-1+d][d] * arr[i] % MOD;
				arr[j] %= MOD;*/

				//cout << "C" << k - 1 + d << ", " << d << "=" << C[k - 1 + d][d] << endl;
			}
		}

		for (int i = 1; i <= n; ++i) {
			if (arr[i] < 0)arr[i] += MOD;
			cout << arr[i] << " ";
		}

		cout << endl;
	}
}


int main() {
	solve();
	return 0;
}
/*
2
8 100
1 2 1 4 1 2 1 8
6 7
1 4 3 17 5 16

2
8 1
1 2 1 4 1 2 1 8
6 2
1 4 3 17 5 16

 */


lld CC(lld n, lld m) {
	lld sum = 1;
	for (int i = n; i > (n - m); --i) sum = sum * i % MOD;
	return sum * inv[m] % MOD;
}

---

本人码农，希望通过自己的分享，让大家更容易学懂计算机知识。创作不易，帮忙点击公众号的链接。