使用通俗易懂的大白话解析：贝叶斯定理、最大似然估计

通俗易懂的大白话解析：贝叶斯定理 & 最大似然估计（MLE）

---

1. 贝叶斯定理（Bayes' Theorem）

一句话解释

贝叶斯定理就是“先有点预判（先验概率），然后拿到新证据，再更新你的判断（后验概率）。”

生活中的例子

例子：感冒 vs. 打喷嚏

假设你在路上看到一个人打喷嚏，你想知道 “他是不是感冒了？” 这时，你可以用 贝叶斯定理 来分析。

• 你对人们感冒的预估（先验概率 P(D)）
  比如，冬天里一般有 10% 的人感冒，所以感冒的概率 P(D) = 0.1。

• 如果感冒了，打喷嚏的概率（P(T|D)）
  假设感冒的人有 80% 的概率会打喷嚏，所以 P(T|D) = 0.8。

• 如果没感冒，打喷嚏的概率（P(T|~D)）
  但有时候人们也会因为灰尘或过敏打喷嚏，假设健康的人有 5% 的概率打喷嚏，所以 P(T|~D) = 0.05。

• 你看到他打喷嚏，这个新信息会影响你的判断（后验概率 P(D|T)）
  贝叶斯定理告诉你：

  

  这里：

  

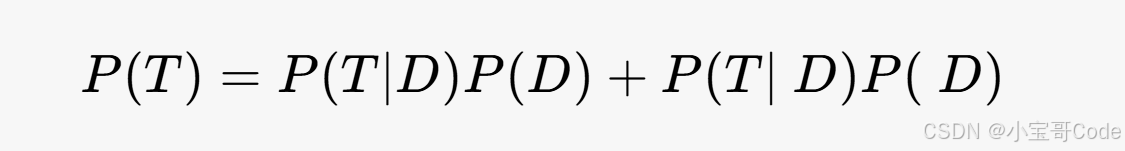
  代入数值计算：

  

  计算后大约是 0.64，也就是说，看到他打喷嚏后，你觉得他感冒的概率从 10% 提高到了 64%！

总结

贝叶斯定理就是 “先有个大致判断（先验），然后根据新证据调整判断（后验）”。
在医学诊断、垃圾邮件过滤、机器学习等领域都很有用！

---

2. 最大似然估计（Maximum Likelihood Estimation, MLE）

一句话解释

“假设你不知道真实情况，但你有一堆数据，你想找到最可能的解释。”

生活中的例子

例子：猜测朋友的口味

假设你有个朋友，他去奶茶店每次都点同样的甜度，但你不知道他最喜欢的是 无糖、少糖、半糖、全糖 哪一种。你决定观察他 10 天的点单数据：

日期	甜度
1	半糖
2	少糖
3	半糖
4	半糖
5	半糖
6	少糖
7	半糖
8	半糖
9	半糖
10	半糖

你发现：

• 他 8 次点了“半糖”
• 他 2 次点了“少糖”
• 他从没点过“无糖”或“全糖”

那么，你最合理的猜测是什么？
他最喜欢的甜度应该是“半糖”！（因为这是他点得最多的）

这就是 最大似然估计（MLE），它的核心思想就是：
“在已知数据的情况下，找到最可能的参数。”

数学解释

最大似然估计的公式是：

意思是：找到使得“观察到的数据”最可能出现的参数。

在上面的例子里，我们想找出 最可能的甜度，所以：

---

3. 贝叶斯 vs. MLE

对比点	贝叶斯定理	最大似然估计（MLE）
主要思想	用新证据更新旧判断	找到最可能的解释
需要先验知识？	要有先验概率	不需要先验知识
适用场景	医学诊断、机器学习、垃圾邮件检测	统计推断、机器学习、参数估计

---

总结

• 贝叶斯定理：“先有猜测 + 看到新证据 = 更新判断”（适合不确定性问题）。
• 最大似然估计（MLE）：“从数据中找到最可能的解释”（适合参数估计）。

希望这个通俗解释能帮到你！