OFDM 十六讲8 Nyquist Zero ISI Theorem

明朝百晓生

于 2022-08-11 11:29:57 发布

阅读量745

点赞数

分类专栏：芯片开发文章标签： servlet java javascript

4AM_明朝百晓生

本文链接：https://blog.csdn.net/chengxf2/article/details/126262187

版权

芯片开发专栏收录该内容

94 篇文章 32 订阅

订阅专栏

前言：

主要参考

因为后面讲 How to Avoid ISI in Digital Communications，涉及到采样定理.

这篇主要讲一下什么是采样，以及采样定理

到目前我们知道ISI 原因主要有两个：

1：多径传输，这个通过CP解决

2： Band Limit 限制，这里从 Nyquist Zero ISI Theorem 分析一下ISI.

因为出身物理专业，对通讯背景知识觉得有所欠缺，又补了一下。

采样定理

跟汽车码表一样，一款硬件的采样频率是有极限的。

根据奈奎采样定理，采样频率必须大于信息频率的2倍，才不会overlap.

如果不做Band-limit 会导致信息的频率非常大，采样频率低于信息频率的2倍，

引起ovelap.

参考：

Neso Academy

Shannon Nyquist Sampling Theorem_哔哩哔哩_bilibili

https://www.youtube.com/watch?v=iQaFDpiNOlA

一采样定义

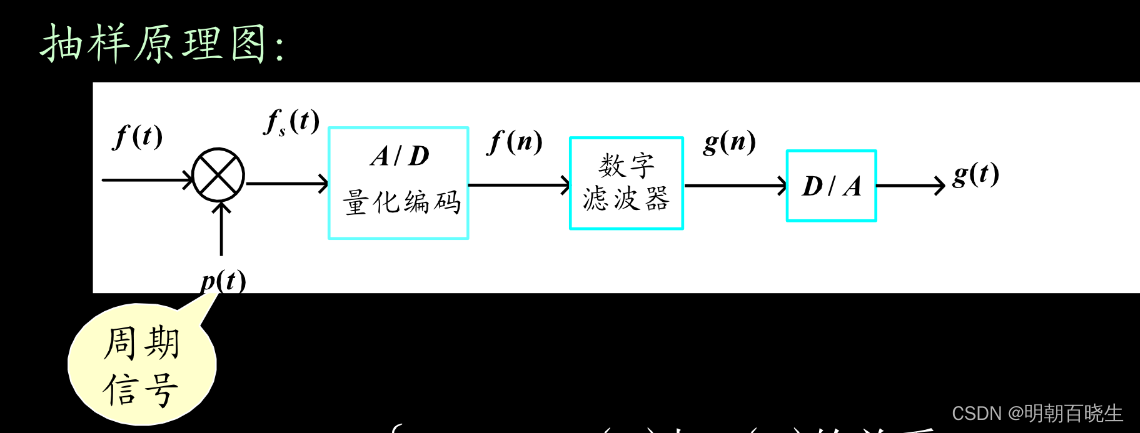
采样定义：

Reduction of continuous time signal to a discrete time signal.

我们使用的是数字通讯系统，连续性时间信号是不存在的，实际使用的是

离散时间信号。

用离散时间信号替代连续时间信号有些限制条件，我们这篇主要讨论

限制条件。

二时域分析

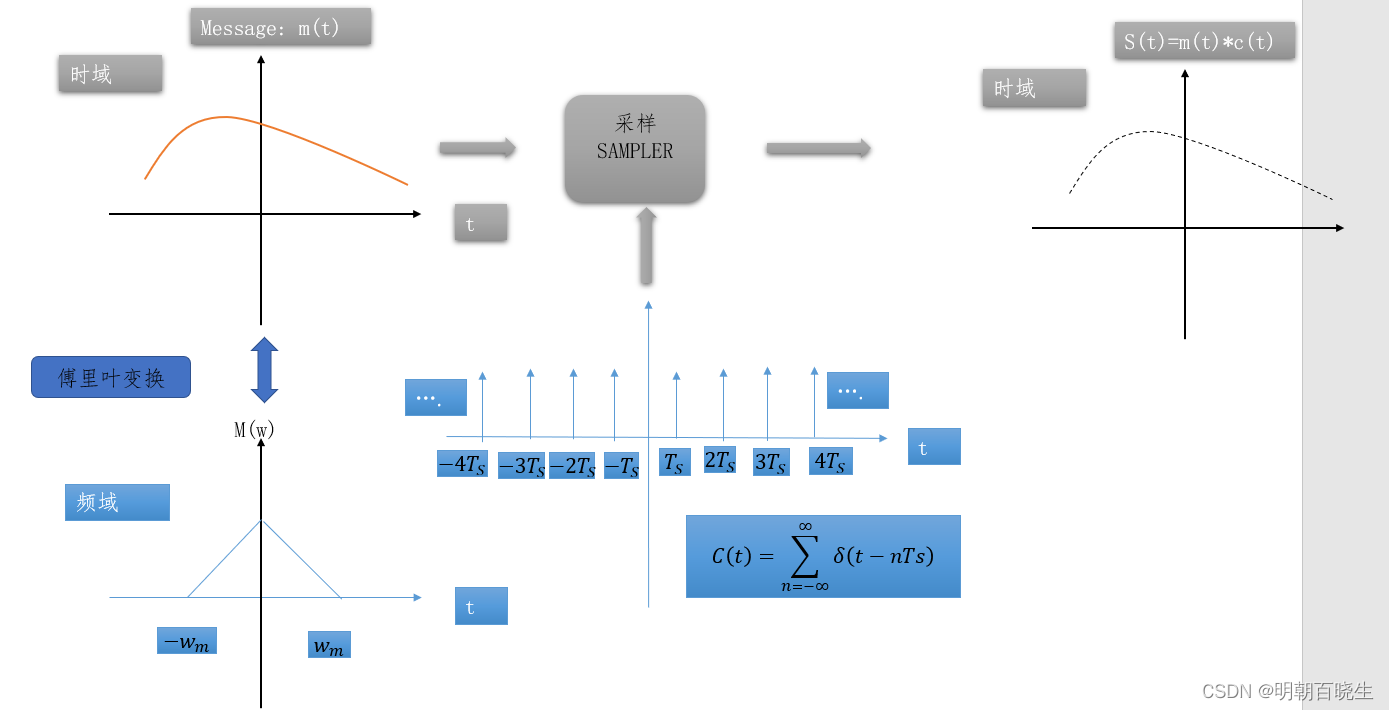
我们输入的信号为m(t),其傅里叶变换如下图M(w)

采样信号为冲激串

$c(t)=\sum_{n=-\infty}^{\infty}\delta(t-nT_s)$

输出信号

$s(t)=m(t)*c(t)$

$=m(nT_s)$

三频域分析

根据时域的乘积对应频域的卷积,输出信号的傅里叶变换为

$s(w)=\frac{1}{2\pi}[M(w)\star c(w)]$

其中采样信号的傅里叶变换为

$c(w)=w_s\sum_{n=-\infty}^{\infty}\delta(w-n w_s)$

则输出信号的傅里叶变换为

$s(w)=\frac{1}{2\pi}[M(w)\star w_s \sum_{-\infty}^{\infty}\delta(w-nw_s)]$

$=\frac{w_s}{2\pi}[\sum_{-\infty}^{\infty} m(w)\star \delta(w-nw_s)]$

$=\frac{1}{T_s}\sum_{n=-\infty}^{\infty}m(w-nw_s)$

上面利用了狄拉克函数的性质4。

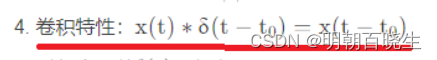
四频域展开（Nyquist Theorem）

$s(w)=\frac{1}{T_s}\sum_{n}m(w-nw_s)$

$=\frac{1}{T_s}[...+m(w+w_s)+m(w+0)+m(w-w_s)+...]$

n>0时候，相当于把频谱右移动 $nw_s$

1: 有GB(guard band) 场景

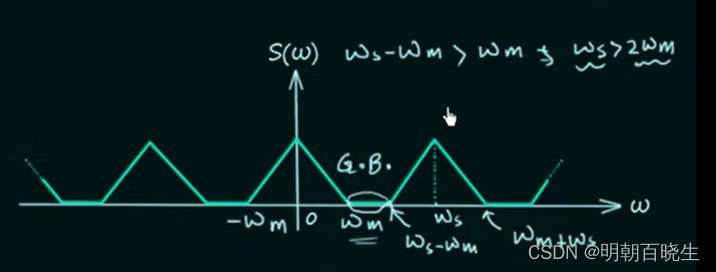
$w_s-w_m>w_m$ , 频谱之间无重叠，相当于有段GB 保护

$w_s>2w_m$

采样信号的频率大于2倍发送信息的频率

$T>2*T_S$ (信息周期要大于2倍个采样周期)

4.2 无GB场景

$w_s=2w_m$

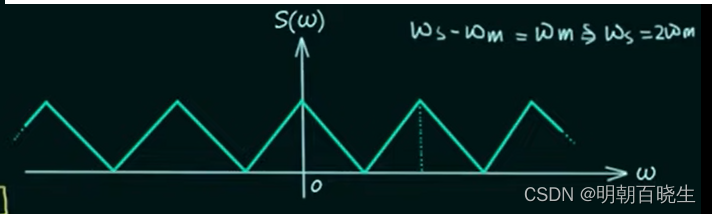
采样频率等于两倍信息的频率

4.3 小于两倍角频率

$w_s< 2w_m$ ,这个时候就有overlap ，产生了干扰。

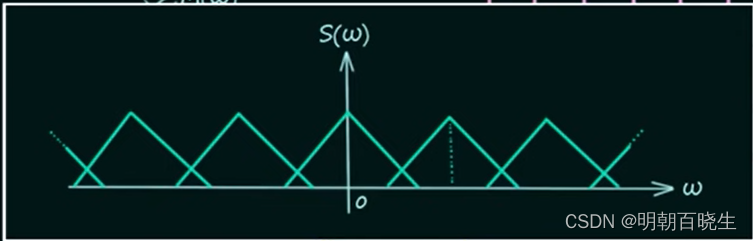
五傅里叶变换补充知识

5.1 傅里叶级数

给定一个周期为T的函数，那么它可以表示为无穷级数

$f(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty}[a_n cos(\frac{2\pi nx}{T})+ b_n sin(\frac{2\pi n x}{T})]$

$=\sum_{n=-\infty} c_n e^{j\frac{2\pi nx}{T}}$

$a_n =\frac{2}{T }\int_{t_0}^{t_0+T}f(t)cos\frac{2\pi n t}{T}dt$

$b_n =\frac{2}{T }\int_{t_0}^{t_0+T}f(t)sin\frac{2\pi n t}{T}dt$

$c_n=\frac{1}{T}\int_{t_0}^{t_0+T}f(t)e^{-j\frac{2\pi nt}{T}}$

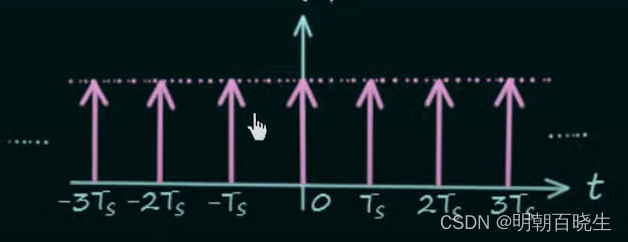
5.2 冲激串定义：

是无限多个分离的周期为的冲激之和，

$s(t)=\sum_{n=-\infty}^{\infty}\delta(t-nT_s)$

$w_s= 2\pi f_s$

5.3 冲击串傅里叶级数

取 $t_0=-\frac{T_s}{2}$ ,计算傅里叶级数系数

$c_n=\frac{1}{T_S}\int_{-T_s/2}^{T_s/2}s(t)e^{-jW_snt}dt$

把上面s(t)展开，根据狄拉克函数的性质

$c_n=\frac{1}{T_s}\int_{- T_s/2}^{T_s/2}\delta(t)e^{-jW_s nt}dt$

$=\frac{1}{T_S}$

则：

$s(t)=\frac{1}{T_S}\sum_{n=-\infty}^{\infty}e^{jW_s nt}$

对其做傅里叶变换

$F(s(t))=\frac{1}{T_S}\int (\sum_{n=-\infty}e^{jW_snt}) e^{-jwt}dt$

$=\sum_{n=-\infty}\frac{2\pi}{2\pi *T_S}\int ( e^{jW_snt}) e^{-jwt}dt$

$=\sum_{n=-\infty}w_s/(2\pi )\int (e^{jW_snt}) e^{-jwt}dt$ 利用公式2

设 $g(w)=2\pi \delta(w-nw_s)$

对其做傅里叶逆变换

$f(t)=\frac{1}{2\pi}\int 2\pi \delta(w-n w_s)e^{jwt}dw$

$=e^{jnw_s t}$

所以 $F(e^{jnw_st})=2\pi \delta(w-nw_s)$ 公式2

把公式2 带入公式1

$F(s(t)) = \sum_{n=-\infty}\frac{w_s}{2\pi}2\pi\delta(w-nw_s)$

$=w_s\sum_{n=-\infty}^{\infty}\delta(w-n w_s)$

狄拉克函数性质：

明朝百晓生

关注

0
点赞
踩
1

收藏

觉得还不错? 一键收藏
0
评论
OFDM 十六讲8 Nyquist Zero ISI Theorem

Nyquist Zero ISI Theorem狄拉克函数，冲激串的傅里叶变换
复制链接

扫一扫

专栏目录

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。