Real-Time Rendering-第四章 Transforms（3）

4.3 Quaternions

虽然四元数早在1843年就由William Rowan Hamilton先生发明出来用于表示复数的扩展，但是直到1985年才由Shoemake[1176]把四元数引入到了计算机图形学领域。四元数是构建具有强大功能的变换操作的一个有力工具，而且在某些方面，四元数是比欧拉角度和矩阵更好的计算方式，特别是在旋转操作和方位计算方面。给定一个 轴&角度 的表示形式，转变成一个四元数或从四元数转变成原来的形式是直截了当的，而使用欧拉角度则无法在任何方向进行转换。四元数可以用于稳定并不断的确定方位的插值运算，而这是使用欧拉角度无法完成的。

复数包含一个实部和一个虚部。每一个部分由两个实数表示，其中第二个实数通过与$\sqrt{-1}$相乘。类似的，四元数具有四个部分。前三个部分的值与旋转轴密切相关，因为旋转的角度会影响所有部分的值（4.3.2节有更多相关的内容）。每一个四元数由4个实数表示，每个实数对应于一个不同的部分。由于四元数具有四个分量，我们选择使用向量的形式表示它们，但是与向量不同的是，在记号上加一个帽子：$\hat{\mathbf{q}}$。首先我们会讨论一些关于四元数的数学背景知识，然后用于构建一些有趣的，实用的变换运算。

4.3.1 Mathematical Background

我们从描述一个四元数的定义开始。
Definition. 可以使用下面的方法定义四元数 $\hat{\mathbf{q}}$，所有的定义都同等的。

$$\qquad\begin{aligned} \hat{\mathbf{q}}\ &= (\mathbf{q}_v, q_w) = iq_x+jq_y+kq_z+q_w=\mathbf{q}_v+q_w,\\ \mathbf{q}_v\ &= iq_x+jq_y+kq_z = (q_x,q_y,q_z),\\ i^2\ &= j^2 = k^2 = -1,\quad jk = -kj = i,\quad ki = -ik = j,\quad ij = -ji = k. \end{aligned} \qquad\qquad \text{(4.28)}$$

其中变量 $q_w$ 称为四元数 $\hat{\mathbf{q}}$ 的实部，虚部为 $\mathbf{q}_v$，并且 $i$，$j$，$k$ 称为虚部的基本单位。

对于四元数的虚部 $\mathbf{q}_v$，我们可以使用向量的所有基本运算，比如向量加法，向量-标量乘法，点乘，叉乘等等。使用四元数的定义，我们推导出两个四元数 $\hat{\mathbf{q}}$ 和 $\hat{\mathbf{r}}$ 的乘法运算，如下所示。需要注意的是虚部的乘法不满足交换律。

$$\qquad\begin{aligned} \text{Multiplication（乘法）：} \\ \hat{\mathbf{q}}\hat{\mathbf{r}}\ &= (iq_x+jq_y+kq_z+q_w)(ir_x+jr_y+kr_z+r_w)= \\ &=i(q_yr_z-q_zr_y+r_wq_x+q_wr_x) \\ &\ \ + j(q_zr_x-q_xr_z+r_wq_y+q_wr_y) \\ &\ \ + k(q_xr_y-q_yr_x+r_wq_z+q_wr_z) \\ &\ \ + q_wr_w-q_xr_x-q_yr_y-q_zr_z = \\ &=(\mathbf{q}_v\times\mathbf{r}_v+r_w\mathbf{q}_v+q_w\mathbf{r}_v,q_wr_w-\mathbf{q}_v \cdot \mathbf{r}_v). \end{aligned} \qquad\qquad \text{(4.29)}$$

从该公式中可以看出，我们同时使用了叉积和点积计算两个四元数的乘积。有了四元数的定义之后，我们就可以定义四元数的加法，共轭，范数，以及单位化运算：

$$\begin{aligned} \text{Addition（加法）:} &\quad\hat{\mathbf{q}}+\hat{\mathbf{r}} = (\mathbf{q}_v,q_w)+(\mathbf{r}_v,r_w)=(\mathbf{q}_v+\mathbf{r}_v,q_w+r_w). \\[2ex] \text{Conjugate（共轭）:} &\quad\hat{\mathbf{q}}^* = (\mathbf{q}_v,q_w)^* = -(\mathbf{q}_v,q_w). \\[2ex] \text{Norm（范数）:} &\quad n(\hat{\mathbf{q}}) = \sqrt{\hat{\mathbf{q}}\hat{\mathbf{q}}^*} = \sqrt{\hat{\mathbf{q}}^*\hat{\mathbf{q}}} = \sqrt{\mathbf{q}_v\cdot\mathbf{q}_v+q_w^2} = \sqrt{q_x^2+q_y^2+q_z^2+q_w^2}. \\[2ex] \text{Identity（单位复数）:} &\quad\hat{\mathbf{i}} = (\mathbf{0},1). \end{aligned} \qquad \text{(4.30)}$$

在对n(\hat{\mathbf{q}}) = \sqrt{\hat{\mathbf{q}}\hat{\mathbf{q}}^*}进行简化（结果如上）之后，虚部都抵消了且只剩下一个实部。四元数的规范化有时也可以表示为|\hat{\mathbf{q}}| = n(\hat{\mathbf{q}})[808]。由以前运算的结果可以推导出四元数的乘法倒数，表示为 $\hat{\mathbf{q}}^{-1}$。倒数必须满足公式$\hat{\mathbf{q}}^{-1}\hat{\mathbf{q}} = \hat{\mathbf{q}}\hat{\mathbf{q}}^{-1} = 1$（这正是乘法倒数的通用性质）。由四元数规范化运算的定义可以推出以下公式：

$$\begin{aligned} n(\hat{\mathbf{q}})^2 = \hat{\mathbf{q}}\hat{\mathbf{q}}^* \Longleftrightarrow \frac{\hat{\mathbf{q}}\hat{\mathbf{q}}^*}{n(\hat{\mathbf{q}})^2} = 1, \end{aligned} \qquad \text{(4.31)}$$

由此可以得到如下的乘法倒数公式：

$$\begin{aligned} \text{Inverse（倒数）:} &\qquad\qquad\hat{\mathbf{q}}^{-1} = \frac{1}{n(\hat{\mathbf{q}})^2}\hat{\mathbf{q}}^*. \end{aligned} \qquad\qquad\qquad\qquad \text{(4.32)}$$

四元数的求导公式使用了标量乘法，这是由公式4.29中的乘法运算推导出来的：$s\hat{\mathbf{q}}=(\mathbf{0},s)(\mathbf{q}_v,q_w)=(s\mathbf{q}_v,sq_w)$，并且$\hat{\mathbf{q}}s=(\mathbf{q}_v,q_w)(\mathbf{0},s)=(s\mathbf{q}_v,sq_w)$，也就是说标量乘法满足交换律。

由四元数的定义可以推导出以下的运算法则：

$$\begin{aligned} \text{Conjugate rules（共轭法则）：} &&(\hat{\mathbf{q}}^*)^* &= \hat{\mathbf{q}}, \\[2ex] &&(\hat{\mathbf{q}} + \hat{\mathbf{r}})^* &= \hat{\mathbf{q}}^* + \hat{\mathbf{r}}^*, \\[2ex] &&(\hat{\mathbf{q}}\hat{\mathbf{r}})^* &= \hat{\mathbf{r}}^*\hat{\mathbf{q}}^*. \end{aligned} \qquad\qquad\qquad\qquad \text{(4.33)}$$

$$\begin{aligned} \text{Norm rules（范数法则）：} &&n(\hat{\mathbf{q}}^*) &= n(\hat{\mathbf{q}}), \\[2ex] &&(\hat{\mathbf{q}} + \hat{\mathbf{r}})^* &= \hat{\mathbf{q}}^* + \hat{\mathbf{r}}^*. \end{aligned} \qquad\qquad\qquad\qquad \text{(4.34)}$$

$$\begin{aligned} &\text{Laws of Multiplication（乘法法则）：} \\[2ex] &\text{Linearity（线性关系）：} &\hat{\mathbf{p}}(s\hat{\mathbf{q}}+t\hat{\mathbf{r}}) &= s\hat{\mathbf{p}}\hat{\mathbf{q}}+t\hat{\mathbf{p}}\hat{\mathbf{r}}, \\[2ex] &&(s\hat{\mathbf{p}} + t\hat{\mathbf{q}})\hat{\mathbf{r}} &= s\hat{\mathbf{p}}\hat{\mathbf{r}} + t\hat{\mathbf{q}}\hat{\mathbf{r}}. \\[2ex] &\text{Associativity（结合律）：} &\hat{\mathbf{p}}(\hat{\mathbf{q}}\hat{\mathbf{r}}) &= (\hat{\mathbf{p}}\hat{\mathbf{q}})\hat{\mathbf{r}}. \end{aligned} \qquad\qquad\qquad\qquad \text{(4.35)}$$

一个四元数 $\hat{\mathbf{q}}=(\mathbf{q}_v,q_w)$为单位四元数，也就是说 $n(\hat{\mathbf{q}})=1$。由此可以把 $\hat{\mathbf{q}}$ 写成如下形式：

$$\begin{aligned} \hat{\mathbf{q}} = (\sin\phi\mathbf{u}_q,\ \cos\phi) = \sin\phi\mathbf{u}_q+\cos\phi, \end{aligned} \qquad \text{(4.36)}$$

对于某些三维向量 $\mathbf{u}_q$，有$\|\mathbf{u}_q\|=1$，因为

$$\begin{aligned} n(\hat{\mathbf{q}}) = n(\sin\phi\mathbf{u}_q,\ \cos\phi) = \sqrt{\sin^2\phi(\mathbf{u}_q\cdot\mathbf{u}_q)+\cos^2\phi} = \sqrt{\sin^2\phi+\cos^2\phi} = 1 \end{aligned} \qquad \text{(4.37)}$$

有且仅有$\mathbf{u}_q\cdot\mathbf{u}_q=1=\|\mathbf{u}_q\|^2$。在下一节我们将会看到，单位四元数非常适合用于高效的创建旋转和定向运算。但在些之前，将会介绍关于四元数的一些额外操作。

对于复数，一个二维的单位向量可以写成$\cos\phi+i\sin\phi=e^{i\phi}$。而对于复数，使用同样的方法表示为

$$\begin{aligned} \hat{\mathbf{q}} = \sin\phi\mathbf{u}_q + \cos\phi = e^{\phi\mathbf{u}_q}. \end{aligned} \qquad \text{(4.38)}$$

由公式4.38可以得到单位四元数的对数和指数运算公式：

$$\begin{aligned} &\text{Logarithm（对数公式）：} &&\log(\hat{\mathbf{q}}) = \log(e^{\phi\mathbf{u}_q}) = \phi\mathbf{u}_q, \\[2ex] &\text{Power（指数公式）：} &&\hat{\mathbf{q}}^t=(\sin\phi\mathbf{u}_q+\cos\phi)^t=e^{\phi\mathbf{u}_q}=\sin(\phi t)\mathbf{u}_q+\cos(\phi t). \end{aligned} \qquad \text{(4.39)}$$

4.3.2 Quaternion Transforms

我们现在开始研究四元数集的一个子类，单位四元数，即那些具有单位长度的四元数。有关单位四元数的最重要的性质是它们可以表示任意的三维旋转，并且这种表示方式极其紧凑简单。

现在我们描述四元数对于旋转和定向操作如此实用的原因。首先把一个点或向量$\mathbf{p}=(p_x\ \ p_y\ \ p_z\ \ p_w)^T$ 4个坐标值存储到一个四元数 $\hat{\mathbf{p}}$ 的四个分量中，并假设有一个单位四元数 $\hat{\mathbf{q}}=(\sin\phi\mathbf{u}_q,\cos\phi)$。则有

$$\qquad\qquad\qquad\qquad\begin{aligned} \hat{\mathbf{q}}\hat{\mathbf{p}}\hat{\mathbf{q}}^{-1} \end{aligned} \qquad\qquad\qquad\qquad\qquad\qquad \text{(4.40)}$$
把四元数 $\hat{\mathbf{p}}$（也就是点 $\mathbf{p}$）围绕轴 $\mathbf{u}_q$ 旋转 $2\phi$ 度。需要注意的是，由于 $\hat{\mathbf{q}}$ 是一个单位四元数，有 $\hat{\mathbf{q}}^{-1}=\hat{\mathbf{q}}^*$。图4.8中演示了该旋转操作，显示这种方法可以用于围绕任意轴旋转。

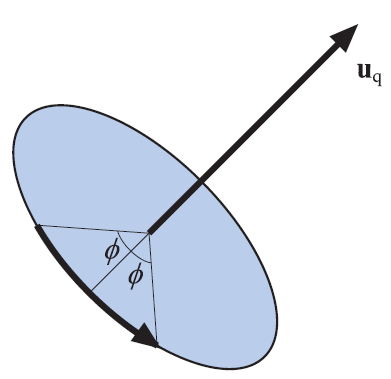
图4.8 使用单位四元数$\hat{\mathbf{q}}=(\sin\phi\mathbf{u}_q,\cos\phi)$表示旋转变换的示例。该变换表示围绕轴 $\mathbf{u}_q$旋转 $2\phi$ 弧度。

四元数 $\hat{\mathbf{q}}$ 任何非0的多个实部也可以表示同样的变换，这意味着 $\hat{\mathbf{q}}$ 和 $-\hat{\mathbf{q}}$ 表示相同的旋转操作。也就是说对轴 $\mathbf{u}_q$ 及实部 $q_w$ 取反，会创建一个与原始四元数旋转结果完全一样的四元数。同样还意味着从一个矩阵中提取出四元数可以是 $\hat{\mathbf{q}}$ 或者 $-\hat{\mathbf{q}}$。

给定两个单位四元数 $\hat{\mathbf{q}}$ 和 $\hat{\mathbf{r}}$，对四元数 $\hat{\mathbf{p}}$（可以用于表示点 $\mathbf{p}$） 首先使用 $\hat{\mathbf{q}}$ 再使用 $\hat{\mathbf{r}}$ 的串联运算，如果公式4.41所示：

$$\qquad\qquad\begin{aligned} \hat{\mathbf{r}}(\hat{\mathbf{q}}\hat{\mathbf{p}}\hat{\mathbf{q}}^*)\hat{\mathbf{r}}^* = (\hat{\mathbf{r}}\hat{\mathbf{q}})\hat{\mathbf{p}}(\hat{\mathbf{r}}\hat{\mathbf{q}})^* = \hat{\mathbf{c}}\hat{\mathbf{p}}\hat{\mathbf{c}}^*. \end{aligned} \qquad\qquad\qquad\qquad \text{(4.41)}$$

其中 $\hat{\mathbf{c}}=\hat{\mathbf{r}}\hat{\mathbf{q}}$ 是一个单位四元数，表示单位四元数 $\hat{\mathbf{q}}$ 和 $\hat{\mathbf{r}}$的串联。

Matrix Conversion

由于一些系统使用硬件的方式实现矩阵乘法，并且这种矩阵乘法比公式4.40更加高效，因此我们需要一种方法用于把一个四元数变换成一个矩阵，反之亦然。把四元数 $\hat{\mathbf{q}}$ 转换成矩阵 $\mathbf{M}^q$，可以使用公式4.42表示

$$\begin{aligned} \mathbf{M}^q = \begin{pmatrix} 1-s(q_y^2+q_z^2) & s(q_xq_y-q_wq_z) & s(q_xq_z+q_wq_y & 0) \\ s(q_xq_y+q_wq_z) & 1-s(q_x^2+q_z^2) & s(q_yq_z-q_wq_x & 0) \\ s(q_xq_z-q_wq_y) & s(q_yq_z+q_wq_x) & 1-s(q_x^2+q_y^2 & 0) \\ 0 & 0 & 0 & 1 \end{pmatrix}. \qquad\qquad\text{(4.42)} \end{aligned}$$
其中标量为 $s=2/n(\hat{\mathbf{q}})$。对于单位四元数，公式4.42可以简化为
$$\begin{aligned} \mathbf{M}^q = \begin{pmatrix} 1-2(q_y^2+q_z^2) & 2(q_xq_y-q_wq_z) & 2(q_xq_z+q_wq_y & 0) \\ 2(q_xq_y+q_wq_z) & 1-2(q_x^2+q_z^2) & 2(q_yq_z-q_wq_x & 0) \\ 2(q_xq_z-q_wq_y) & 2(q_yq_z+q_wq_x) & 1-2(q_x^2+q_y^2 & 0) \\ 0 & 0 & 0 & 1 \end{pmatrix}. \qquad\qquad\text{(4.43)} \end{aligned}$$
使用四元数构建了矩阵之后，没有任何三角函数需要计算了，因此在实际运算过程中这种变换过程是非常高效的。

反过来，从一个正交矩阵 $\mathbf{M}^q$ 变换为单位四元数 $\hat{\mathbf{q}}$ 则需要更多运算。该运算过程的关键是由公式4.43中的矩阵得到的不同点：

$$\qquad\qquad\begin{aligned} m_{21}^q-m_{12}^q &= 4q_wq_x,\\ m_{02}^q-m_{20}^q &= 4q_wq_y,\\ m_{10}^q-m_{01}^q &= 4q_wq_z. \end{aligned} \qquad\qquad\qquad\qquad \text{(4.44)}$$
这些公式所表示的含义是，如果 $q_w$ 是已知的，就可以计算向量 $\mathbf{v}_q$的值，因此可以推导出 $\hat{\mathbf{q}}$。使用如下公式可以计算矩阵 $\mathbf{M}^q$ 的迹
$$\qquad\begin{aligned} \mathrm{tr}(\mathbf{M}^q) &= 4-2s(q_x^2+q_y^2+q_z^2) = 4\left(1-\frac{q_x^2+q_y^2+q_z^2}{q_x^2+q_y^2+q_z^2+q_w^2}\right) \\ &= \frac{4q_w^2}{q_x^2+q_y^2+q_z^2+q_w^2} = \frac{4q_w^2}{n(\hat{\mathbf{q}})}. \end{aligned} \qquad\qquad \text{(4.45)}$$
由此可以得到如下单位四元数的转换公式：
$$\qquad\qquad\begin{aligned} q_w=\frac{1}{2}\sqrt{tr(\mathbf{M}^q)}, && q_x=\frac{m_{21}^q-m_{12}^q}{4q_w}, \\ q_y=\frac{m_{02}^q-m_{20}^q}{4q_w}, && q_z=\frac{m_{10}^q-m_{01}^q}{4q_w}. \end{aligned} \qquad\qquad \text{(4.46)}$$

为了得到一个数值稳定的例程，需要避免除以较小的数。因此，首先设置$t=q_w^2-q_x^2-q_y^2-q_z^2$，由此可以得到如下公式

$$\qquad\qquad\begin{aligned} m_{00} &= t+2q_x^2,\\ m_{11} &= t+2q_y^2,\\ m_{22} &= t+2q_z^2,\\ u &= m_{00}+m{11}+m_{22} = t+2q_w^2. \end{aligned} \qquad\qquad \text{(4.47)}$$
也就是说最大的 $m_{00},m_{11},m_{22}$ 和 $u$ 值反过来可以确定 $q_x,q_y,q_z$ 和 $q_w$ 也是最大的。如果 $q_w$ 为最大值，则可以使用公式4.46除四元数。否则，我们需要注意以下公式：
$$\qquad\qquad\begin{aligned} 4q_x^2 &= +m_{00}-m_{11}-m{22}+m_{33},\\ 4q_y^2 &= -m_{00}+m_{11}-m{22}+m_{33},\\ 4q_z^2 &= -m_{00}-m_{11}+m{22}+m_{33},\\ 4q_w^2 &= \mathrm{tr}(\mathbf{M}^q). \end{aligned} \qquad\qquad \text{(4.48)}$$
然后使用上面适用的公式计算 $q_x,q_y$ 和 $q_z$ 的最大值，之后再使用公式4.44计算四元数 $\hat{\mathbf{q}}$ 的其余分量值。幸运是已经有相关的代码用于转换的计算，见本章末尾的Further Reading and Resources。

Spherical Linear Interpolation

Spherical Linear Interpolation（球面线性插值）是指，给定两个单位四元数 $\hat{\mathbf{q}}$ 和 $\hat{\mathbf{r}}$，以及一个参数 $t\in[0,1]$，计算一个插值四元数的操作。比如在处理动画物体时这种操作非常实用。但是对于相机朝向的插值运算该操作并不实用，因为相机的“向上方向”的向量在插值过程中会发生倾斜，通常产生一种令人不快的效果。

这种插值操作的代数形式可以使用如下的组合四元数 $\hat{\mathbf{s}}$ 表示：

$$\qquad\qquad\begin{aligned} \hat{\mathbf{s}}(\hat{\mathbf{q}},\hat{\mathbf{r}},t) = (\hat{\mathbf{r}}\hat{\mathbf{q}}^{-1})^t\hat{\mathbf{q}}. \end{aligned} \qquad\qquad\qquad\qquad \text{(4.49)}$$
但是对于使用软件实现来说，使用以下的形式更合适，其中 slerp 表示球面线性插值：
$$\qquad\qquad\begin{aligned} \hat{\mathbf{s}}(\hat{\mathbf{q}},\hat{\mathbf{r}},t) = \mathrm{slerp}(\hat{\mathbf{q}},\hat{\mathbf{r}},t) = \frac{\sin(\phi(1-t))}{\sin\phi}\hat{\mathbf{q}} = \frac{\sin(\phi t)}{\sin\phi}\hat{\mathbf{r}}. \end{aligned} \qquad\qquad\qquad\qquad \text{(4.50)}$$

要计算该公式中所需要的 $\phi$ 值，可以使用如下论据：$\cos\phi=q_xr_x+q_yr_y+q_zr_z+q_wr_w$[224]。对于任意的 $t\in[0,1]$，slerp函数用于计算插值的两个四元数从 $\hat{\mathbf{q}}(t=0)$ 到 $\hat{\mathbf{r}}(t=1)$ 一起构成了四维单位球面上的最短圆弧。该弧线位于由 $\hat{\mathbf{q}}$、$\hat{\mathbf{r}}$及球心所有的平面，与四维单位球的相交形成的圆圈上。如图4.9所示。由些计算得到的旋转四元数以恒定的速度围绕一个固定轴旋转。这种具有恒定速度的旋转曲线， 加速度为0，称为 geodesic 曲线[263]。

slerp函数非常适用于在两个朝向向量之间进行插值，并且计算结果非常稳定（保持固定轴，恒定速度）。在使用多个欧拉角度进行插值时无法达到这种运算效果。在实际运算过程中，直接执行slerp运算需要调用大量的三角函数，是一种高计算成本的操作。为此，Li[771，772]提出改进的方法，在不牺牲任何精度的情况下可以更快速的计算slerps值。

当有多个表示朝向的四元数可以用时，比如$\hat{\mathbf{q}}_0$，$\hat{\mathbf{q}}_1$，$\cdot\cdot\cdot$，$\hat{\mathbf{q}}_{n-1}$，并且我们要从 $\hat{\mathbf{q}}_0$ 到 $\hat{\mathbf{q}}_1$ 再到 $\hat{\mathbf{q}}_2$ 进行插值，依此类推，直接到 $\hat{\mathbf{q}}_{n-1}$，可以使用一连串的slerp运算。假设现在要计算 $\hat{\mathbf{q}}_i$，我们将会使用 $\hat{\mathbf{q}}_{i-1}$ 和 $\hat{\mathbf{q}}_i$ 作为slerp的参数。计算完 $\hat{\mathbf{q}}_i$ 之后，就使用 $\hat{\mathbf{q}}_i$ 和 $\hat{\mathbf{q}}_{i+1}$ 作为下一个slerp运算的参数。这会导致在对朝向向量进行插值过程中出现急剧的变动，如图4.9所示。这种方法类似于对多个点进行线性插值；详见原书578页图13.2的右上图。一些读者在阅读第13章有关样条曲线的描述之后可能会回过头来学习以下段落。

一种更好的插值计算方法是使用某种样式的样条曲线。首先我们引入介于 $\hat{\mathbf{q}}_i$ 和 $\hat{\mathbf{q}}_{i+1}$ 之间的四元数 $\hat{\mathbf{a}}_i$ 和 $\hat{\mathbf{a}}_{i+1}$。然后使用 $\hat{\mathbf{q}}_i$，$\hat{\mathbf{a}}_i$，$\hat{\mathbf{a}}_{i+1}$ 和 $\hat{\mathbf{q}}_{i+1}$ 组成的四元数集定义三次球面插值运算。令人惊奇的是，使用如下的公式可以计算这些额外的四元数[294]：

$$\qquad\qquad\begin{aligned} \hat{\mathbf{a}}_i = \hat{\mathbf{q}}_i\mathrm{exp}\left[-\frac{\log(\hat{\mathbf{q}}_i^{-1}\hat{\mathbf{q}}_{i-1}) + \log(\hat{\mathbf{q}}_i^{-1}\hat{\mathbf{q}}_{i+1})}{4}\right]. \end{aligned} \qquad\qquad\qquad\qquad \text{(4.51)}$$
其中 $\hat{\mathbf{q}}_i$ 和 $\hat{\mathbf{a}}_i$ 用于对四元数进行球面插值，使用公式4.52所示的光滑的三次样条曲线：
$$\qquad\begin{aligned} \mathrm{saurd}(\hat{\mathbf{q}}_i,\hat{\mathbf{q}}_{i+1},\hat{\mathbf{a}}_i,\hat{\mathbf{a}}_{i+1},t) = \mathrm{slerp}(\mathrm{slerp}(\hat{\mathbf{q}}_i,\hat{\mathbf{q}}_{i+1},t),\mathrm{slerp}(\hat{\mathbf{a}}_i,\hat{\mathbf{a}}_{i+1},t),2t(1-t)). \end{aligned} \qquad \text{(4.52)}$$

如上公式所示，$\mathrm{slerp}$ 函数由多次重复使用slerp进行球面插值运算构成（详见第13章13.1.1节有关对多个点进行重复线性插值的讲解）。插值将会在初始的朝向四元数 $\hat{\mathbf{q}}_i,i\in[0,\cdot\cdot\cdot,n-1]$之间进行传递，但是不会在 $\hat{\mathbf{a}}_i$ 中传递，这些新引入的四元数用于表示初始四元数的切线方向。

插值将通过传递
初始方向 ˆqi，我 ∈ [0，…，n−1]，但不是通过 ˆai — — 这些都是
用于指示在初始取向的切线方向