目录
2. 同构(isomorphism)和同态(homomorphism)
0. 前言
业余爱好小白的群论自学笔记。没有目的,为了学习而学习。用自己能够理解的方式沿着自己的思路进行整理记述(东施效颦小平邦彦的抄书学数学),不求严谨完备,但求逻辑连贯。
1. 群的定义
【定义1】:二元运算(binary operator)
一个从非空集合A到非空集合B的二元运算将集合A中的一个有序对(a1,a2)映射到集合B中的一个元素b,即
.
通常我们用“” 或者 “
”来表示二元运算符,这样
就可以写成:
或者
。但是,要记住,它只是二元运算符的抽象表示,并不等同于我们通常熟悉的乘法符号,虽然后者的确是二元运算符的一种。甚至,在不会引起混淆的情况下,省略任何符号直接记为
表示a和b经二元运算所得结果。在本系列中,以上多种记号都会出现,通常根据上下文可以知道所表达的意思。
同理,三元运算符表示将A集合的一个有序三元组映射到集合B中的一个元素。二元运算可以用“” 或者 “
”来表示,三元或更多元的运算就只能用
的形式来表示了,
的形式是更为通用的映射表示方式。
【定义2】:封闭性(closedness)
一个二元运算符在集合A上封闭,当且仅当,对A中任意两个元素a和b,经过
运算后的结果仍然在集合A中,即
.
也就是,映射的像(image)是A的一个子集。
【定义3】:群的公理性定义
在集合G上定义一个二元运算,如果满足以下4条性质,则称它们构成一个群,记为(G,
):
- 二元运算
在G上满足封闭性
- 二元运算
在G上满足结合律。
- G中包含二元运算*的单位元(Identity)。
- G中包含二元运算*逆元(Inverse)。
注1,群的公理性质并不包括交换律。满足交换律的群称为阿贝尔群(为纪念尼尔斯.阿贝尔,群论奠基人之一),或者交换群。绝大多数的群都不是阿贝尔群。整数集在整数加法下构成一个阿贝尔群
注2,在不会引起混淆的场合,(G,*)通常就简记为群G。但是一定要记住,脱离了二元运算谈论群就是讨论无根之木、无源之水。比如说,对于整数集,在加法下构成一个群,记为 (
,+);但是在减法、乘法、除法下就不构成群。
2. 同构(isomorphism)和同态(homomorphism)
【定义4】同态
如果一个映射在群
和群
的运算下满足:
称该映射为一个群同态映射(简称同态)。
群的结构归根结底由群的二元运算所决定。根据以上定义,同态映射与群运算的顺序可以颠倒,先做群运算再做映射和先做映射后再做群运算所得到的结果相等。因此,我们可以说同态映射保持了群的(运算)结构。
进一步,如果同态映射既是单射(injection),还是满射(surjection),即它是双射(bijection,满足一一对应关系),它就升级为同构映射(isomorphism)了。
【定义5】同构
一个同态映射 如果可逆,则称它是G到H的同构映射。如果G和H之间存在同构映射,则称G和H同构,记为
,简记为
.
同构,从字面上理解就是相同的结构。两个群同构意味着两者具有完全相同的结构。
同态非常广泛,但是通常意义不大。我们研究更多的是同构。从数学的角度来看,两个群同构的话,意味着它们具有完全相同(等价)的结构,仅仅是对元素分配了不同的标签、对运算不同的名字而已,可以把它们看成一样的。由于同构映射是可逆的,我们可以先对G的两个元素进行(G上的)运算,或者也可以在先映射到H上,对H上的两个对等元素进行(H上的)运算,然后再经过逆映射回到G,这样会得到相同的结果。即:
顺便提一下,熟悉傅里叶变换的小伙伴或许记得(卷积定理,这里表现的是离散形式,其中表示圆卷积):
是不是长得很像?这个算是群同构的一种具体实例吗?
例(群同构):定义集合, 容易验证,该集合在加法运算下构成一个群,记为(
, +)。考虑一个映射从
,且
. 容易验证这个映射满足以上同构的要求,因此有
.
3. 有限群
【定义6】有限群
群(G,*)的阶(order)记为,表示G中元素的个数。如果G中元素个数有限,换句话说G为有限集,则称群(G,*)为有限群。
,两个整数的模n加法(modular addition)运算为
。经过模n加法运算的结果必为0到n-1之间的某个整数,记0到n-1之间的整数的集合为
,容易证明,该集合在模n加法(modular addition)运算下构成一个有限群,记为
。
4. 循环群(Cyclic Group)
循环群是最基本的群族。那什么是循环群呢?
【定义7】群的幂运算
对于群(G,*)中的任意元素a,定义a的n次幂为:
,
a在括号内出现n次。
【定义8】群元素的阶
令e表示群(G,*)的单位圆,则群元素a的阶定义为使得的最小正整数,记为|a|,即:
.
注意,不要混淆了群的阶(参见[定义6])和群元素的阶!
【定义9】循环群的生成
如果集合包含了G的所有元素,称a生成群(G,*),且群(G,*)的阶等于a的阶,即:
。能够以这种方式生成的群即为循环群。a称为(G,*)的生成元。
并非所有群都能以这种方式(一个元素不断地重复运算)生成。只有循环群能够通过一个生成元生成,其它的群都需要两个或以上的生成元生成。但是,需要注意的是,虽然循环群能够通过一个生成元生成,生成元却并不是唯一的!
群的生成元类似于线性空间的基,线性空间可以由不同的基张成,一个群同样可以由不同的生成元(集合)生成。可能“群由生成元生成”是“线性空间由基张成”更为底层的概念,后者是前者的一种具体实例(?),只不过我们通常学习数学(特别是非科班)的路径可能都是先学习了线性空间后才会接触到抽象代数和群,所以反而是先了解了线性空间由基张成的概念。
根据以上定义,循环群必为有限群。循环群的单位元即为。
[Q1] 有没有可能存在大于k的自然数j,使得a的j次方不在集合中呢?结论当然是不存在,否则的话以上定义就不成立了。证明如下:
循环群的例子
上述的即为一个循环群(以下就简记为
)。
令, z称为1的n次方根(n-th root of unity)。容易证明,对任意自然数n,1的n次方根在乘法运算下构成一个循环群。
循环群可以用于描述物体的旋转对称。如下图所示是一张正方形的卡片,如果只考虑该卡片在平面上的旋转的话,容易知道将该卡片旋转90、180、270、360度后会与原卡片重合。我们称这是正方形满足在平面上做k*90度旋转操作下的对称性。

图1 正方形卡片的旋转对称
显而易见,正方形在平面上的k*90度旋转操作构成一个4元循环群,这个群的元素为:旋转零度(单位元,记为rot0);顺时针旋转90度(记为rot90);顺时针旋转180度(记为rot180);顺时针旋转270度(记为rot270)。
显然,rot90可以作为该群的生成元,因为
以上三个循环群事实上是同构的。事实上,更进一步,
【定理1】任何阶数n的循环群都同构于 .
.
证明:To be added.
因此,事实上你可以认为只有一种阶数为n的循环群,记为,甚至就直接用
代表n阶循环群也完全可以!
群的可视化之一:凯莱表(乘法表)
群的常用可视化方式有三种:(1) 凯莱表;(2)凯莱图;(3)循环图。这里我们先介绍前两种。循环图留到后面介绍。凯莱表把群看作集合上的二元运算,以各元素两两运算的结果制成表格即得凯莱表。
以n = 4为例, 模4加的Cayley Table(凯莱表)如下所示:

Cayley Table也称为Structure Table,Multiplication Table(乘法表,乘法表的说法可能更常见)。这是因为这个表的确长得像我们所熟悉的乘法表。但是总觉得这个确实有那么一点点misleading,对加法不太公平的感觉哈^-^。就说这个例子吧,明明就是(模4)加法嘛,怎么就成了乘法表呢(嗯,虽然我知道是什么意思,但是我还是觉得中性的Cayley Table或Structure Table更合适一些)
群的可视化之二:凯莱图
凯莱图把群看作作用的集合。以上面正方形的旋转对称为例。

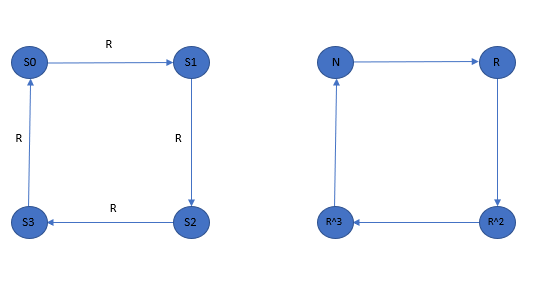
图2 凯莱图
(左):以状态为节点的凯莱图;
(中): 左图的形式化(抽象化);
(右):以作用路径为节点的凯莱图
关于凯莱图的制作及其所表达的意义等,在【2】中花费了很多笔墨进行讲解,建议想进一步了解的小伙伴一定去读原书(有中文版)。不过原书中将(右)图称为作用图,似乎要与凯莱图区分开来。不过我觉得还是统一称为凯莱图,只不过是两种不同表现形式(侧重点不同)的凯莱图而已(不知道是不是有理解错误),从左到右的抽象程度也是越来越高。
小结
本文中介绍了群的公理性定义、群同构、有限群以及最基本的有限群--循环群,以及群的可视化技术之凯莱图和凯莱表等概念。
下一篇准备介绍基于简单的群构造复杂的群,比如说,直积(Direct Sum)和直和(Direct Sum);以及反过来将复杂的群分解为简单的群,比如说,陪集,因子群,商群等相关概念。并相应地逐步介绍一些更复杂一些的群,比如说,对称群,二面体群,等等。
2022-01-31 以此篇结束牛年博客灌水活动^-^
本群论学习笔记系列总目录:
群论基础速成(5):生成元,凯莱图,轨道,循环图,以及群的“维度”?
参考文献:
【1】Sam Kennerly,A Crash Course In Group Theory--Part I: Finite Groups
【2】Nathan Carter, Visual Group Theory. (中文版:《群论彩图版》)
【3】Michael Artin, ALGEBRA

























 2102
2102

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










