概率机器人<3>_C7 定位-localization

Abbr:

 TBD

牢记

重点

中文书 ：page160

复习： 地图类型 2中（feature base, location base <occupancy grid> ）

高精地图的创建有2种方式：

众包（分布式）-每辆汽车 自身实时定位，建立实时地图回传云端，在云端完成大数据整合，分享其它车辆。 时效性好，精度一般--mobileye 为代表

分包：地图商专业车辆事先采集的地图在云端分发。无时效性，精度高。--高德，百度

 

---

概念定义：

确定机器人相对于地图（绝对地图，或自身创建的实时地图）的姿态（位置和方向--6自由度），经常也叫“位置估计” 。也就是，状态估计。

定位属于感知的范畴。解决了“在哪儿”的基本感知问题。 在之前的马尔科夫链图中加入地图信息m ,m 是先验已知的。

前提假设: 地图信息准确，已知  (如何创建地图?后面章节会介绍），且环境是静止的，不随时间变化。地图以全局坐标系描述，独立于机器人位姿。

---

如何定位：定位是建立地图坐标系与机器人局部坐标系一致性的过程， R|t  坐标转换的过程。 

坐标系统一后，（pose_in ego ）---R|t ---> (pose_in map) , 获得的新的pose。就是ego的位置。

位姿确定性吗？：可是一次测量的ego pose 就能确定吗？  “想象一下，机器人位于一幢建筑物内，且该建筑内有许多相似的走廊而一次传感器测量（如一次测距扫描）通常不足以识别具体是哪条走廊。”--因此需要综合多次测量结果，匹配，才能 定位。

因此，一次测量不足以确定ego的姿态。 

---

定位问题分类：

全局定位vs局部定位

• position tracking （算法难度△）： 局部定位，初始位姿已知（在地图中的绝对位姿已知） 难度△
• global localization （算法难度△△）: 初始位姿未知
• kidnapped problem （算法难度△△△）: 属于全局定位的变种，程序安全性考虑）测量的位姿和实际位姿不一致。 比如测量的代码被黑客篡改，或程序出现bug, “机器人被绑架 瞬间移动到其他位置” ，因为机器人可能相信知道自己在哪儿，尽管它不是在那里。--来衡量该算法从全局定位失效中恢复的能力。

动态环境vs静态环境：周围环境不变：静态，易于定位，如果环境变化（比如家具移动，门开关 ..）建模复杂。

---

Markov Localization 马尔可夫定位 算法框架：

基于贝叶斯滤波器 的一种简单的概率定位算法，称之为 马尔科夫定位 。算法如下：<回顾一下上面的那张图片>

notes: 就是加入了先验的地图m信息。在贝叶斯滤波器的框架中。算法适合解决全局，追踪，绑架 问题。

前提：环境是静止的。

---

一个具体事例： 相当经典！！

回顾一下前面说的几个重要的点： 重复场景的地图中（符合实际情况-很多东西都类似，重复的），初始姿态未知， 一次测量时无法实现准确定位的。下面用一个有“多个同样门的走廊 ”来说明马尔科夫定位是如何实现的。

0.初始化： 位姿x 在空间上出现的概率-均匀分布（已知）， 1/N  (N 代表空间分割的颗粒数）-如果用栅格表示的，N就是总栅格数

记做，bel '(x0)

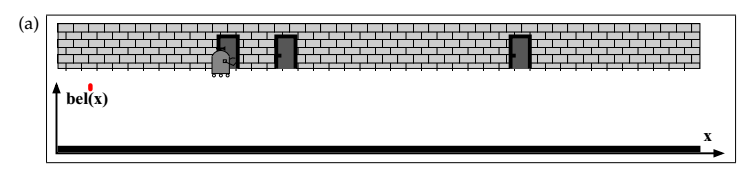
某个时刻x1，某个位姿x1， （图中机器人走到了门边）

①第一次测量：结果如下，测量概率模型p(z|x)--测量 --灰色（已知），（这个场景下，每个门出现概率是1/3）,相乘叠加后

①测量更新：bel(x1)=bel'(0) * 测量概率 ， (黑色）

② 运动预测：机器人继续运动。预测 bel'(x2)= 转移概率*bel(x1)  （2个概率相乘，变得更小）--下图变矮了。

③ 第二次测量：在新的位姿 x2处，进行新的测量，

③测量更新：bel(x2) = 测量概率* bel'(x2)  ，黑色

和上一个图合起来看：，就是通过概率的加权，提高精度。（注意获得的概率分布狭窄。--方差变小（实现了2个大的方差加权，获得一个小的方差）。！）--准确的说法：两个独立估计值的整合比每一个孤立的估计值应该使得机器人确定性更高