主成分分析法
主成分分析是利用降维的思想,在损失很少信息的前提下,把多个指标转化为几个综合指标的多元统计方法。通常把转化生成的综合指标称为主成分,其中每个主成分都是原始变量的线性组合,且各个主成分之间互不相关,使得主成分比原始变量具有某些更优越的性能。这样在研究复杂问题时就可以只考虑少数几个主成分而不至于损失太多信息,从而更容易抓住主要矛盾,揭示事物内部变量之间的规律性,同时使问题得到简化,提高分析效率。
目录
- 基本思想
- 基本理论
- 引入一般方法
- 主成分分析步骤
- 关于学习方法的一些个人见解
- 从协方差矩阵出发求解主成分
- 从相关矩阵出发求解主成分
- 关于由协方差矩阵或相关矩阵出发求解主成分的选取问题
- 关于模型中的一些问题
基本思想
在对某一事物进行实证研究时,为了更全面、准确地反映事物的特征及其发展规律,人们往往要考虑与其有关系的多个指标,这些指标在多元统计中也称为变量,这样就产生了如下问题:
- 一方面人们为了避免遗漏重要的信息而考虑尽可能多的指标;
- 另一方面考虑指标的增多增加了问题的复杂性,同时由于各指标均是对同一事物的反映,不可避免地造成信息的大量重叠,这种信息的重叠有时甚至会抹杀事物的真正特征与内在规律。
基于上述问题,人们就希望在定量研究中涉及的变量较少,而得到的信息量又较多。
既然研究某一问题涉及的众多变量之间有一定的相关性,就必然存在着起支配作用的共同因素。根据这一点,通过对原始变量相关矩阵或协方差矩阵内部结构关系的研究,利用原始变量的线性组合形成几个综合指标(主成分),在保留原始变量主要信息的前提下起到降维与简化问题的作用,使得在研究复杂问题时更容易抓住主要矛盾。
一般来说,利用主成分分析得到的主成分与原始变量之间有如下基本关系:
- 每一个主成分都是各原始变量的线性组合;
- 主成分的数目大大少于原始变量的数目;
- 主成分保留了原始变量的绝大多数信息;
- 各主成分之间互不相关。
通过主成分分析,可以从事物之间错综复杂的关系中找出一些主要成分,从而能有效利用大量统计数据进行定量分析,解释变量之间的内在关系,得到对事物特征及其发展规律的一些深层次的启发。
基本理论
设对某一事物的研究涉及p个指标,分别用X1, X2, .... , Xp表示,这p个指标构成的p维随机变量为X = (X1, X2, .... , Xp)T。设随机变量X的均值为μ,协方差矩阵为∑。
对X进行线性变换,可以形成新的综合变量,用Y表示,也就是说,新的综合变量可以由原来的变量线性表示,即满足下式:
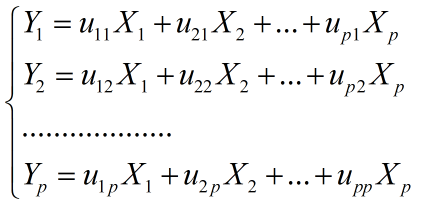
由于可以任意地对原始变量进行上述线性变换,由不同的线性变换得到的综合变量Y的统计特性也不尽相同。因此为了取得较好的效果,我们总是希望Yi=ui.T*X的方差尽可能大且各Yi之间相互独立,由于

而对任意的常数c,有
![]()
因此对ui不加限制时,可使var(Yi)任意增大,问题将变得没有意义。我们将线性变换约束在下面的原则之下:

- Yi与Yj相互无关
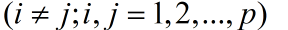
- Y1是X1,X2,... , Xp的一切满足原则(1)的线性组合中方差最大者;Y2是与Y1不相关的X1,X2,... , Xp所有线性组合中方差最大者;........ Yp是与Y1,Y2,.... , Yp-1都不相关的X1,X2,... , Xp的所有线性组合中方差最大者。
基于以上三条原则确定的综合变量Y1,Y2,.... , Yp分别称为原始变量的第一、第二.....第p个主成分。其中,各综合变量在总方差中所占的比重依次递减。在实际研究工作中,通常只挑选前几个方差最大的主成分,从而达到简化系统结构、抓住问题实质的目的。
引入一般方法
主成分分析的基本思想就是在保留原始变量尽可能多的信息的前提下达到降维的目的,从而简化问题的复杂性并抓住问题的主要矛盾。而这里对于随机变量X1,X2,... , Xp而言,其协方差矩阵或相关矩阵正是对各变量离散程度与变量之间相关程度的信息的反映,而相关矩阵不过是将原始变量标准化后的协方差矩阵。我们所说的保留原始变量尽可能多的信息,也就是指生成的较少的综合变量(主成分)的方差和尽可能接近原始变量方差的总和。因此在实际求解主成分的时候,总是从原始变量的协方差矩阵或相关矩阵的结构分析入手。一般来说,从原始变量的协方差矩阵出发求得的主成分与从原始变量的相关矩阵出发求得的主成分是不同的。
主成分分析步骤
- 根据研究问题选取初始分析变量
- 根据初始变量特性判断由协方差阵求主成分还是由相关矩阵求主成分;
- 求协方差阵或相关阵的特征值与相应标准特征向量;
- 判断是否存在明显的多重共线性,若存在,则回到第(1)步;
- 得到主成分的表达式并确定主成分个数,选取主成分;
- 结合主成分对研究问题进行分析并深入研究。
关于学习方法的一些个人见解
- 对一个方法或模型进行理论分析和研究可以让我们从原理层面更加深入理解方法的逻辑和规则,如果运气好,还可以知道这个方法为什么要这么做,有什么意义,这会让我们在对实际问题进行分析时能够更加的灵活多变。
- 但是过度的理论研究会让我们深陷泥潭,无法自拔,往往会把简单的问题复杂化,而忘记学习方法的初心,即解决实际问题。
- 所以,从简单的实际问题入手,结合理论与实际应用进行学习,是最高效的学习途径。
从协方差矩阵出发求解主成分
接下来抛开繁琐的理论,直接通过示例的计算来展示主成分方法的计算过程。
例一:设随机变量X=(X1, X2, X3)T的协方差阵为:

试求X的主成分及主成分对变量Xi的贡献率ρi(i=1,2,3)
解:首先求∑的特征值和对应的正交特征向量,由
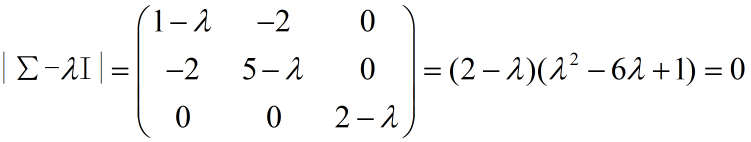
得∑的特征值为![]() ,
,![]() ,
,![]() 。
。
当![]() 时,解方程组
时,解方程组

得相应的单位正交特征向量为:

当![]() 时,解方程组
时,解方程组

得相应的单位正交特征向量为:
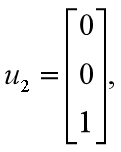
当![]() 时,解方程组
时,解方程组

得相应的单位正交特征向量为:
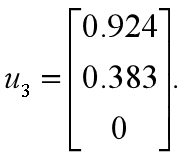
所以,主成分为
![]()
![]()
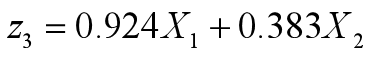
当m=1时,Z1对X的贡献率为:
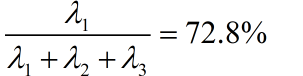
取m=2时,Z1,Z2对X的贡献率为
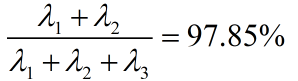
如果前m个主成分的贡献率达到80%~90%,表明取前m个主成分基本包含了全部测量指标所具有的信息,这样既减少了变量的个数又便于对实际问题的分析和研究。
下面通过程序来实现对特征值和特征向量的求解:
A = np.mat([[1, -2, 0],
[-2, 5, 0],
[0, 0, 2]])
evals, evecs = np.linalg.eig(A)
print("特征值:", evals)
print("特征向量:", evecs)结果为:
特征值: [ 0.17157288 5.82842712 2. ]
特征向量: [[-0.92387953 0.38268343 0. ]
[-0.38268343 -0.92387953 0. ]
[ 0. 0. 1. ]]
Process finished with exit code 0从相关矩阵出发求解主成分
例二:设随机变量X=(X1, X2, X3)T的协方差阵为

试以其相关矩阵R求X的主成分、第一主成分的贡献率及第一与第二主成分的累积贡献率。
分析:这里涉及到由协方差阵向相关矩阵的转换,我会详细叙述数学算术解法与程序实现(非常详细)。
解:先摆上关键公式:
![]()
根据公式首先我们需要求解出协方差阵的对角元素矩阵的标准差矩阵,额,可能比较啰嗦,我写出来你就明白了。
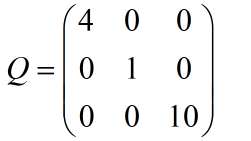
然后,我们需要写出Q的逆矩阵,关于逆矩阵的求解方法,有两种:
可以计算出Q的逆矩阵为

所以,可以根据公式计算出相关矩阵R


程序实现:
B = np.mat([[16, 2, 30],
[2, 1, 4],
[30, 4, 100]])
# 由协方差阵计算相关系数矩阵
# 1、先计算协方差矩阵的尺寸
xieFangChaZhen = B
length = len(xieFangChaZhen)
# 2、生成一个与协方差矩阵同大小的单位矩阵
e = np.eye(length)
# 3、计算方差矩阵,其实就是利用单位矩阵消除协方差矩阵中的非对角线元素
variance = np.multiply(e, xieFangChaZhen)
# 4、求得标准差矩阵
Q = np.sqrt(variance)
# 5、求得标准差的逆矩阵
Q_1 = np.linalg.inv(Q)
# 6、根据公式就求得了相关系数矩阵
xiangGuanZhen = np.dot(np.dot(Q_1, xieFangChaZhen), Q_1)
print('相关矩阵为:\n', xiangGuanZhen)结果为:
相关矩阵为:
[[ 1. 0.5 0.75]
[ 0.5 1. 0.4 ]
[ 0.75 0.4 1. ]]
Process finished with exit code 0再根据相关矩阵R求解特征值和特征向量,然后求解主成分与累积贡献率等,与上一个例题求解步骤相同,这里就不赘述了。
关于由协方差矩阵或相关矩阵出发求解主成分的选取问题
一般而言,对于度量单位不同的指标或取值范围彼此差异非常大的指标,不直接由其协方差矩阵出发进行主成分分析,而应该考虑将数据标准化。
对原始数据进行标准化处理后倾向于各个指标的作用在主成分的构成中相等。对于取值范围相差不大或度量相同的指标进行标准化处理后,其主成分分析的结果仍与由协方差出发求得的结果有较大区别。其原因是由于对数据进行标准化的过程实际上也就是抹杀原始变量离散程度差异的过程,标准化后的各变量方差相等,均为1,而实际上方差也是对数据信息的重要概括,也就是说,对原始数据进行标准化后抹杀了一部分重要信息,因此才使得标准化后变量在对主成分构成中的作用趋于相等。由此看来,对同度量或取值范围在同量级的数据,还是直接从协方差矩阵求解主成分为宜。
建议在实际工作中分别从不同角度出发求解主成分并研究其结果的差别,看看是否发生明显差异且这种差异产生的原因在何处,以确定用哪种结果更为可信。
关于模型中的一些问题
协方差矩阵与相关矩阵的求解问题:
可以使用numpy模块中的cov方法求解。在已知原始变量数据的问题上,可以通过numpy模块中的corrcoef方法求解相关矩阵。
原始变量数据的标准化问题:
对同一变量单位的改变会产生不同的主成分,主成分倾向于方差大的变量的信息,方差小的变量就可能体现得不够,也存在“大数吃小数”的问题。为了使主成分分析能够均等地对待每一个变量原始数值,消除由于单位不同可能带来的影响,我们常常对各原始变量进行标准化处理。对数据进行标准化处理,以使每一个变量的均值为0,方差为1。 数据标准化后,总体的协方差矩阵与总体的相关系数矩阵相等。
关于数据的规范化,我会在以后的博客中详细叙述。
在没进行数据标准化的前提下,从相关矩阵求得的主成分与协差阵求得的主成分一般情况下是不同的。实际表明,这种差异有时很大。如果各指标间的数量级相差较大,特别是各指标有不同的量纲,较为合理的做法就是用相关系数矩阵代替协差阵。对于经济问题所涉及的变量大部分都是不统一的,采取R代替协差阵后,可以看作是用标准化的数据做分析,这样使得主成分分析有实际意义。不仅便于剖析实际问题,又可以避免异常数据的影响。
方法在实际问题中的应用问题:
利用主成分分析法在实际问题处理应用中,其实还有很多要注意的事项,比如数据的预处理,变量的选取问题,模型的分析与解释等,本文只是简单的叙述了关于主成分分析的一些关键步骤的解法,缺乏深入的解读和实际问题的应用,这些问题将会在以后的学习中逐步解决。
参考:
多元统计分析/何晓群编著. -4版. --北京:中国人民大学出版社,2015.3







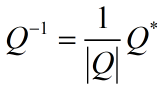














 393
393

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








