LBD算法 - Graph matching 图匹配算法分析

最新推荐文章于 2024-09-11 15:13:30 发布
最新推荐文章于 2024-09-11 15:13:30 发布
阅读量1.4w 收藏 33
点赞数 5
分类专栏： 经验 学习 文章标签： 算法 测试

概述

原文：《An efficient and robust line segment matching approach based on LBD descriptor and pairwise geometric consistency》

上一步我们进行了线特征的提取和描述，接下来我们进行线特征的匹配。在此之前我们先通过预处理将一些明显无法匹配的特征给消除，以降低图匹配问题的维度。
该部分图匹配算法分为三步：

  1. 查找候选匹配对
  2. 构建关系图
  3. 生成最终匹配结果

1. 查找候选匹配对

匹配的双方，我们分别称为参考图像和查询图像，检测出双方的LineVecs之后，我们要检测他们的一元几何属性和局部外观相似度，若未通过测试，那么认为他们是不匹配的。这样做可以大大减小图优化匹配的问题维度，使得我们后期匹配的速度更快。

1.1.一元几何属性

线段的一元几何属性就是LineVecs的方向，在同一个LineVec中的线具有相同的方向，并且每一个LineVec拥有唯一的方向。但是两张图中的LineVecs的方向有可能是不可靠的，图像有可能会有任意角度的旋转，对于这点，我们利用图像对之间存在的近似全局旋转角，可以减少候选匹配对的数目。

构建旋转

和其他文章中使用对应匹配来进行图像旋转不同，LBD的Matching中通过计算两个图像的LineVecs方向直方图，得到规范化直方图，h代表直方图。我们改变的角度，通过公式寻找一个全局近似旋转角。

而全局旋转变换不一定总是好的，所以我们也需要去检查估计旋转角是不是真的。实际上如果透视变换可以通过旋转来近似，那么直方图之差比较小。这代表了在进行了旋转之后，两个图像之间的相似程度。
这里写图片描述
上图就显示出了两张图之间的直方图差距，通过旋转我们可以得出两张图之间相似度很高。上图中的预估角度是0.349，偏移是0.243

但是如果图像中提取的线重复度很低的话，这种直方图方法就有可能提取出错误的旋转角度。为了解决这个问题，对于在方向直方图上落入相同区间bins的线段，将他们的长度累积起来。那么我们就可以得到一个长度向量，其第i个元素就是方向直方图中第i个bin中的线段累计长度。

我们设定最小偏移直方图小于阈值th，并且最小偏移长度向量距离小于阈值tl时，我们接受我们所估计的全局旋转角。一旦全局旋转角被接受，就会有一对LineVecs被匹配。但是如果这对LineVecs的方向角度和估计的全局旋转角之差超过阈值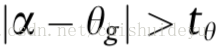，那么我们认为他们是不能够匹配的。如果两个图片之间没有可以接受的旋转角度，那么我们只测试他们的外观相似性。

1.2. 局部外观相似性

我们用直线描述符之间的距离（lost）来度量局部外观相似度。
对于LineVec中的每个线段，我们都从提取出线的尺度层中生成一个LBD描述子向量V。当我们对一幅图像中提取出来的两组LineVec进行匹配，要去评估参考LineVec和测试LineVec中所有描述子之间的距离，并且用最小的描述子距离去测量LineVec外观相似度s。如果 s > ts s大于局部外观不相似容忍度，那么相应两个LineVecs将不会再进一步考虑。

在检查了LineVecs的一元几何属性和局部外观相似性之后，通过了这些测试的直线对被当做候选匹配。我们在上面的测试中，应当选取一组松散阈值，其中经验值是 tθ=π/4 ts=0.35。候选匹配的数量比实际匹配的数量要大很多，因为我们不能仅仅按照刚才两个属性来确定最终的匹配结果，当然我们上面的工作也是大大减小了图形匹配的问题维度的。

2. 构建关系图

对于上面得到一组候选匹配项，我们要构建一个关系图
其中关系图里的节点代表潜在的对应点
节点之间的连接的权重代表对应点之间的一致性。

拿到了k对对应关系，我们用一个大小为k*k的邻接矩阵A来表示关系图，其中第i行第j列的元素值是候选LineVec匹配对的一致性得分。其中分别是引用图和查询图的LineVecs变量，上面的一致性得分是通过候选匹配对的成对几何属性和外观相似度计算的来的。

成对几何属性


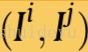
我们选择两条线分别是，他们代表了这两个LineVecs之间的最小描述子距离，并在原图中定位他们的端点位置。然后我们用他们的交点比率，投影比率和相对角度来描述的几何属性，就如上图所描述的那样。其中的两个值的计算方法如下：

Ij和Pj的值可以用相同的方法求解得到，相对角度可以直接用线方向求得。这三个量对平移旋转缩放都是不变的。

外观相似度

之前，我们使用LBD描述向量来表示线的局部外观。
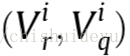
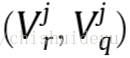
假设描述子与r图（参考图）和q图（查询图）的LineVecs之间的最小距离是，同理对是。我们可以得到两组成对几何属性和局部外观，分别是。

计算一致性得分Aij：



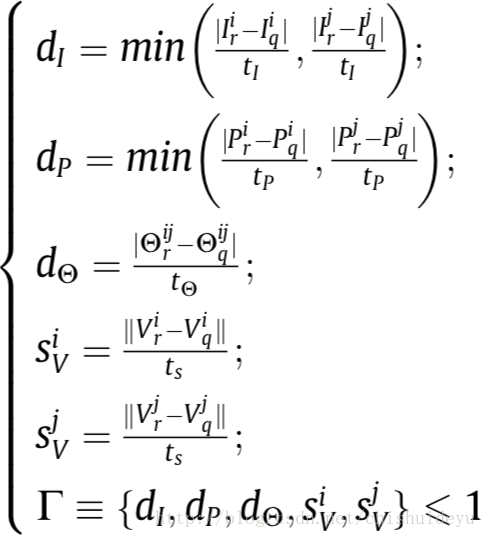
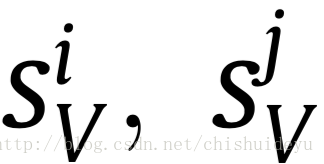
其中是几何相似性；是局部外观相似性；是条件。最后一个代表所有在内的元素都不能大于1。
接下来我们设。计算完他们的一致性得分之后，我们便获得了邻接矩阵A。

3. 生成最终匹配结果

到这一步之后，匹配的问题最终就变成了，寻找匹配簇LM，该匹配簇可以最大化总的一致性分数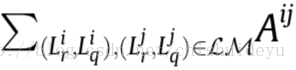，以至于可以满足映射约束。我们使用一个指标向量来表示这个簇，否则为0，因此这个问题被表示为：

其中x受制于映射约束。一般来说用二次规划来解决这个问题太耗费资源，我们采用谱图技术，对x放款映射约束和积分约束，使得他的元素可以采集实际值在[0,1]区间里。
通过Raleigh比率定理，可以最大化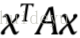的x*是A的主特征向量。它仍然是使用映射约束二值化特征向量和获得最优解的一个强大近似。

以下是算法细节：

  1. 通过EDLine算法从参考图和查询图内提取LineVecs，以从两幅图中分别获得两组LineVecs
  2. 利用两组LineVecs的方向直方图估计图像对的全局旋转角
  3. 计算两组LineVecs的LBD描述子
  4. 通过检查描述子的一元几何属性和局部外观，生成一组候选匹配对
  5. 根据候选匹配对中一致性分数，构建k*k大小的邻接矩阵
  6. 通过使用ARPACK库，得到邻接矩阵A的主特征向量x*
  7. 初始化匹配结果
  8. 查找，如果x*(a)=0，那么停止查找返回匹配结果LM，否则设，且x*(a)=0。
  9. 检查CM中所有的候选者，如果和冲突，那么设
  10. 如果CM是空的，那么返回LM，否则返回到步骤8。

最后一行的线段匹配可以从LineVecs LM的匹配结果直接检索。注意，在LineVec的线位于图像的同一区域，并且具有同一方向，因此，每对linevec的匹配，线段匹配有一对就足够检索了。

参考文档：
http://www.cnblogs.com/Jessica-jie/p/7545554.html

代码：
https://github.com/chishuideyu/LBD_and_LineMatching

Xue Feng BUPT
关注
专栏目录
线特征---LBD算法（三）
a7691176的博客
09-14 1248
上一节主要是介绍LSD算法理论，这节主要是介绍LBD算法。 参考文章：An efficient and robust line segment matching approach based on LBD descriptor and pairwise geometric consistency ----Lilian Zhang , Reinhard Koch 第二部分：Li...
lsd 特征点匹配代码_线特征LSD and 描述子LBD---LBD算法（二）
weixin_39588223的博客
12-20 1399
上一节主要是介绍LSD算法理论，这节主要是介绍LBD算法。1.尺度空间中提取线段为了克服在线检测碎片问题和提高大尺度变化的性能，我们的检测框架采用由对原始图像进行搞死下采样(with a set of 尺度因子and 高斯模糊 )的尺度空间金字塔组成(N层图像)。我们首先用Edline算法每层的尺度空间产生一组线。每一条直线都有一个方向，它是由从直线左边到右边的大部分边缘像素的梯度构成的。然后通...
破解子图匹配难题，10 万奖金等你来领
最新发布
华为云官方博客
09-11 1014
华为持续赞助全球重大科技竞赛，开放业界前沿研究课题，旨在促进科技人才培养，持续赋能科技企业，进一步推动科技进步和产业发展。
线特征基础（LSD算法、LBD描述子、普朗克坐标）
fxmtb的博客
04-07 1491
线特征基础（LSD算法、LBD描述子、普朗克坐标）
北大邹磊：图数据库中的子图匹配算法
DataFun_Hoh的博客
04-18 5982
本文从图数据库中的核心查询算子——子图匹配入题，介绍了图数据库的基本概念、子图匹配的算法，以及在图数据库环境下的子图匹配查询优化等内容。
Graph Matching
AIWCZ的博客
10-11 1763
受严骏驰老师讲座内容启发，最近项目中一个关键问题才找到了一些解决途径，为了能够快速对Graph Matching的起源和发展现状有一定了解，从而形成知识体系来更好得解决问题，准备慢下来，把这些知识沉淀下来，写成一篇blog。 (讲座链接：https://www.bilibili.com/video/BV1Zf4y1S7Zr) Graph Matching 属于一种组合优化问题，图这类数据结构形式在推荐系统、知识图谱等中最为常见，而在计算机视觉领域中，为解决少样本学习或目标检测类别长尾分布等，图结构也有较多工
图匹配算法
07-28 2897
一、二分图匹配图匹配里面最特殊的一种就是二分图匹配，当然，也是算法最简单的一种。所谓二分图，用最通俗的说法，就是图的顶点恰好可以分成两个集合，同一个集合内的顶点间不允许有边，处在不同集合的顶点允许有边相连。而二分图匹配，指的是，从整个二分图中选出若干条边，图中的任意一个顶点（对于
图的最大匹配算法
weixin_34082177的博客
11-06 859
定义：在一个无向图中，定义一条边覆盖的点为这条边的两个端点。找到一个边集S包含最多的边，使得这个边集覆盖到的所有顶点中的每个顶点只被一条边覆盖。S的大小叫做图的最大匹配。 二分图的最大匹配算法：设左边集合为A集合，有边集合为B集合。二分图最大匹配常用的有两种方法。 （1）第一种方法叫做匈牙利算法。这个方法依次枚举A中的每个点，试图在B集合中找到一个匹配。对于A集合中一点x，假设B集合中有一个与...
c# 联合halcon 基于相关性 模板匹配_Python-OpenCV 17. 图像匹配算法
weixin_39977776的博客
11-20 615
本系列文章是学习《机器学习实践指南 案例应用分析 第2版》的笔记。一、定义图像匹配是通过对影像内容、特征、结构、关系、纹理及灰度等的对应关系，相似性和一致性的分析，寻求相似影像目标的方法。匹配分类1. 灰度匹配(模板匹配)灰度匹配的基本思想:以统计的观点将图像看成是二维信号，采用统计相关的方法寻找信号间的相关匹配。利用两个信号的相关函数，评价它们的相似性以确定同名点。灰度匹配通过利用某种相似性度量...
线特征_LSD直线检测算法和LBD直线描述子
惊鸿一博
01-05 1183
线特征在于具有天然的光照及视角不变性，同时更高级的特征也使追踪的鲁棒性和准确性有所提高。特别是在特定的人造场景（室内，走廊）等场景，能够克服无纹理或者不可靠纹理带来的干扰。线段的检测及匹配耗时相对特征点更大。同时在后端也没有一个标准且通用的SLAM优化及回环模块。线特征匹配也是较为困难的，如线段易断裂，不具备强有力的几何约束（如极线几何约束），在纹理缺失处不具有较强的辨识度等。同一条直线在不同视角下的观测不稳定，由于遮挡、直线特征提取算法等因素的影响，直线的端点不具有重复性，同一直线特征可能断裂。
Graph Matching Networks for Learning the Similarity of Graph Structured Objects
05-07
近日，DeepMind 和谷歌联合进行了一项研究，该研究提出了一种执行相似性学习的新型强大模型——图匹配网络（GMN），性能优于 GNN 和 GCN 模型。该论文已被 ICML 2019 接收。 DeepMind 和谷歌的这项新研究聚焦检索和匹配图结构对象这一极具挑战性的问题，做出了两个重要贡献。 首先，研究者展示了如何训练图神经网络（GNN），使之生成可在向量空间中执行高效相似性推理的图嵌入。其次，研究者提出了新型图匹配网络模型（GMN），该模型以一对图作为输入，通过基于跨图注意力的新型匹配机制进行联合推理，从而计算它们之间的相似性分数。 研究者证明 GMN 模型在不同领域中的有效性，包括极具挑战性的基于控制流图的函数相似性搜索问题，这个问题在检索软件系统的漏洞中起着非常重要的作用。实验分析表明 GMN 模型不止能在相似性学习的环境下利用结构，还能超越针对这些问题手动精心设计的特定领域基线系统。研究主题：图相似性学习问题 图是编码关系结构的自然表征，常常出现在多个领域中。根据图结构数据定义的计算可以用在各种领域中，从计算生物学和化学的分子分析到自然语言理解中知识图或图结构解析的分析都可以。 近几年来，图神经网络（Graph Neural Network，GNN）已经成为可以有效学习结构数据表征、解决各种基于图的监督预测问题的模型了。这样的模型在迭代聚合局部结构信息的传播过程中设计并计算图节点表征，从而对图元素的排列（permutation）具有不变性。然后直接将这些节点表征用于节点分类，或者将它们合并到用于图分类的图向量中。而 GNN 在监督分类或回归以外的问题的相关研究相对较少。 DeepMind 的这篇论文研究的是图结构对象的相似性学习问题，这个问题在现实生活中有很多重要的应用，尤其是在图数据库中基于相似性的搜索。还有一个应用是涉及计算机安全的二元函数相似性搜索，给定的二元函数可能包含有已知漏洞的代码，我们要检查这个二元函数中是否有和已知易受攻击的函数相似的控制流图（control-flow-graph）。这有助于识别闭源软件中易受攻击的静态连结函式库，这是一个很常见的问题 (CVE, 2010; 2018)，现在还没有很好的解决方法。图 1 展示了一个例子，在这个例子中用汇编语言注释的控制流图来表示二元函数。这种相似性学习问题极具挑战性，因为就算是图之间细微的差别也会造成语义上极大的不同，但结构不同的图语义上可能非常相似。因此，对这个问题而言，一个成功的模型应该（1）利用图结构；（2）能从图的结构和学习到的语义中推导出图的相似性。图 1：二元函数相似性学习问题。检查两个图是否相似需要推理图的结构和语义。左边两个控制流图对应使用不同编译器编译的相同函数（因此二者比较相似），但右侧图对应的是不同函数。 解决方案 为了解决图相似性学习问题，该论文研究了 GNN 在这种情况中的使用，探讨了如何用 GNN 将图嵌入到向量空间，并学习这种嵌入模型，从而使向量空间中相似的图靠近、不相似的图分开。这个模型的一个重要特性是它可以将每一个图独立地映射到一个嵌入向量，然后在向量空间中执行相似性计算。因此，可以预先计算并索引大型数据库中的图嵌入，这样就能用快速的最近邻搜索数据结构（如 k-d 树） 或局部敏感哈希算法 (Gionis et al., 1999) 执行高效的检索。 研究者进一步扩展 GNN，提出新型图匹配网络（Graph Matching Networks，GMN）来执行相似性学习。GMN 没有单独计算每个图的图表征，它通过跨图注意力机制计算相似性分数，来关联图之间的节点并识别差异。该模型依赖成对图计算图表征，因此它比嵌入模型更强大，并在准确率和计算之间做出了很好的权衡。 研究者在三个任务上评估了 GMN 和基线模型：仅捕获结构相似性的合成图编辑距离学习任务（synthetic graph edit-distance learning tas），以及两个现实世界任务——二元函数相似性搜索和网格检索，这两项任务都需要推理结构相似性和语义相似性。在所有任务中，GMN 都比基线和结构不可知（structure agnostic）模型的性能更好。在更详细的模型简化测试中，研究者发现 GMN 始终优于图嵌入模型和 Siamese 网络。 该研究的贡献如下： 展示了如何用 GNN 产生用于相似性学习的图嵌入； 提出了新型图匹配网络（GMN），该网络基于跨图注意力匹配来计算相似性； 实验证明，该研究提出的图相似性学习模型 GMN 在多个应用中都有良好的表现，比结构不可知模型和现有的手动建立的基线模型都要好。 深度图相似性学习 给定两个图 G1 = (V1, E1) 和 G2 = (V2, E2)，我们需要一个可以计算两图之间相似性分数 s(G1, G2) 的模型。每个图 G = (V, E) 被表示为节点 V 和边 E 的集合，每个节点 i∈V 都可以和特征向量 x_i 相关联，每条边 (i, j) ∈ E 都可以和特征向量 x_ij 关联起来。这些特征可以表示节点类型、边的方向等。如果一个节点或者一条边不能关联任何特征，那么我们可以将对应向量设置成值为 1 的常量。研究者提出了两个图相似性学习模型：一个是基于标准 GNN 的学习图嵌入的模型；另一个是更为崭新也更加强大的 GMN。图 2 展示了这两个模型：图嵌入模型 图嵌入模型可以将每一个图都嵌入到向量中，然后用向量空间中的相似性矩阵衡量图之间的相似性。GNN 嵌入模型包括三个部分：编码器、传播层和聚合器。 图匹配网络 图匹配网络以一对图作为输入，计算它们之间的相似性分数。和嵌入模型相比，图匹配模型联合成对图计算相似性分数，而不是先将每个图独立地映射到向量上。因此，图匹配模型可能比嵌入模型更加强大，但它需要额外的计算效率。 图匹配网络改变了每个传播层中的节点更新模块，这样不仅可以考虑到每个图的边上的聚合信息，还可以考虑到衡量一个图中的一个节点和其他图中的一或多个节点匹配近日，DeepMind 和谷歌联合进行了一项研究，该研究提出了一种执行相似性学习的新型强大模型——图匹配网络（GMN），性能优于 GNN 和 GCN 模型。该论文已被 ICML 2019 接收。 程度的跨图匹配向量：以调整图的表征，在它们不匹配时放大它们之间的差异。 实验 研究者在三个任务上评估了图相似性学习（Graph Similarity Learning，GSL）框架、图嵌入模型（GNN）以及图匹配网络（GMN）的性能，并将这些模型与其他方法进行了对比。总体上，实验结果表明在图相似性学习任务上，GMN 表现优异，而且始终优于其他方法。 学习图编辑距离（GED) 图 G1 和 G2 之间的图编辑距离即将 G1 变换为 G2 所需的最小编辑操作。通常这些编辑操作包括添加／移除／替换节点和边。图编辑距离是衡量图之间相似性的自然指标，在图相似性搜索中有很多应用。 从下表 1 中可以看出，通过学习特定分布的图，GSL 模型的性能优于一般的基线模型，而 GMN 的性能持续优于图嵌入模型（GNN）。基于控制流图的二元函数相似性搜索 二元函数相似性搜索是计算机安全领域中的重要问题。当我们无法获取源代码时，可以通过二元函数执行分析和搜索，例如在处理商业或嵌入式软件或可疑的可执行程序时。 下图 4 展示了具备不同传播步和不同数据设置的不同模型在二元函数相似性搜索任务上的性能。从图中，我们可以看到： 图嵌入模型和图匹配模型的性能随着传播步的增加而持续提升； 在传播步足够的情况下，图嵌入模型持续优于基线模型； 图匹配模型在所有设置和传播步的情况下都优于图嵌入模型。研究者检测了GMN 模型中不同组件的效果，并将 GMN 模型与图卷积网络（GCN）、图神经网络（GNN）和 GNN/GCN 嵌入模型的 Siamese 版本进行对比。 下表 2 展示了实验结果，表明： GNN 嵌入模型是具备竞争力的模型（比 GCN 模型强大）； 使用 Siamese 网络架构基于图表征学习相似性要比使用预先指定的相似性指标（Euclidean、Hamming 等）好； GMN 优于Siamese 模型，这表明在计算过程早期进行跨图信息交流是非常重要的。
图像匹配算法总结
04-22
包含一个总结图像匹配的文献与一个实现图像匹配的经典算法链接，是理解图像匹配算法的很好的资料。
几种图像匹配算法
11-10
几种图像匹配算法：图像匹配 最小二乘 基于灰度 相关系数，包括思想和实现
lsd 特征点匹配代码_直线匹配-LSD算法
weixin_39996035的博客
12-20 693
转自https://www.cnblogs.com/Jessica-jie/p/7523364.html参考文章：An efficient and robust line segment matching approach based on LBD descriptor and pairwise geometric consistency ----Lilian Zhang , Reinhard ...
匈牙利算法
pussy_foot
08-28 788
转自：二分图的最大匹配、完美匹配和匈牙利算法这篇文章讲无权二分图（unweighted bipartite graph）的最大匹配（maximum matching）和完美匹配（perfect matching），以及用于求解匹配的匈牙利算法（Hungarian Algorithm）；不讲带权二分图的最佳匹配。二分图：简单来说，如果图中点可以被分为两组，并且使得所有边都跨越组的边界，则这就是一个二分
C. Dynamic Graph Matching
海边拾贝，沧海一粟
07-31 609
C. Dynamic Graph Matching 题意 C. Dynamic Graph Matching 题意 给定一个 n 个点的无向图，m 次加边或者删边操作。 在每次操作后统计有多少个匹配包含 k = 1, 2, …,n/2 条边。 匹配的定义： 边的集合，没有共同的顶点 先把匹配的概念转换，n个边的匹配，就是n条边没有共同的顶点，那就是2...
图匹配（Graph Matching）入门学习笔记——以《Factorized Graph Matching》为例（三）
深视
09-28 2929
本文主要介绍了与图匹配问题非常相似的点配准（Point Registration）问题，分析了二者之间的区别和联系。原文作者没有提点配准问题，而是用了ICP(Iterative Closest Point)的说法，但我个人认为ICP只是求解三维点配准的一种方法，使用点配准这个概念应该更加准确。最后介绍了如何将几何约束引入FGM中来求解可变形图（Deformable Graph）的匹配问题。
图匹配（Graph Matching）入门学习笔记——以《Factorized Graph Matching》为例（一）
热门推荐
深视
09-24 1万+
这篇文章本身是图匹配经典论文《Factorized Graph Matching》的阅读笔记，后来发现该文介绍并串联了许多图匹配相关的知识，甚至可以看作一个小小的综述性文章，因此就作为图匹配的学习笔记了。因为笔者本人才疏学浅，对于图匹配也是刚刚开始接触，所以文章内容难免存在纰漏和错误，也欢迎各位朋友批评指正。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值