服务价值特征分布的演化预测

问题描述：挖掘不同服务价值特征（评价实体）并计算权重值，生成在各个时间段的分布情况。通过已知的时间序列分布，预测未来某个时刻的服务价值特征权重值。

数据的形式如下图所示：

每一行表示一个服务价值特征（评价实体），每一列表示一段时间，比如某一个月、某一天等等，每一列是严格按照时间顺序由远及近排列的。假设我们的目标是预测上图中month_j+1这一列中的所有数值（也可以预测更加久远的，不过意义不大且精度差）。

解决思路

这个问题我一般看大数据竞赛中有没有相似的赛题，很显然是有的，只不过数据不一样，不过要做的事情是一样的，也就是进行数值型预测。

由于未来的那个时间段并没有发生，也就是说没有任何的特征。一般有两种解决思路：1）基于机器学习的回归预测（滑窗法） 2）基于时间序列的预测。

技术方案

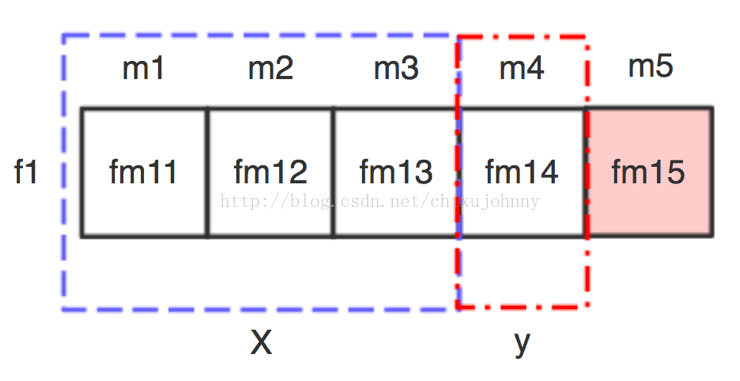
1）基于机器学习的回归预测（滑窗法）：每个样本是服务价值特征，每个feature是时间，样本在每个feature下的值为该时间段内这个服务价值特征积累的权重值总和。滑窗法形如下图所示：

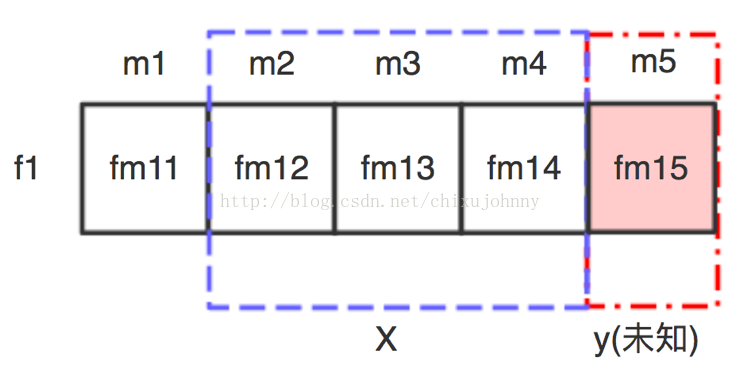
月份m1~m4已知，求m5的预测值。先建模，假设滑窗大小=3，则使用m1~m3作为输入X，m4作为目标值y，拟合一套模型。再用m2~m4作为输入X，m5作为目标值y，将X扔进刚才建好的模型中就可以输出m5的预测值了。当然还有很多细节问题需要在实验中解决，比如滑窗大小的选择，回归模型的选择（目前暂定随机森林和GBRT），模型参数等。

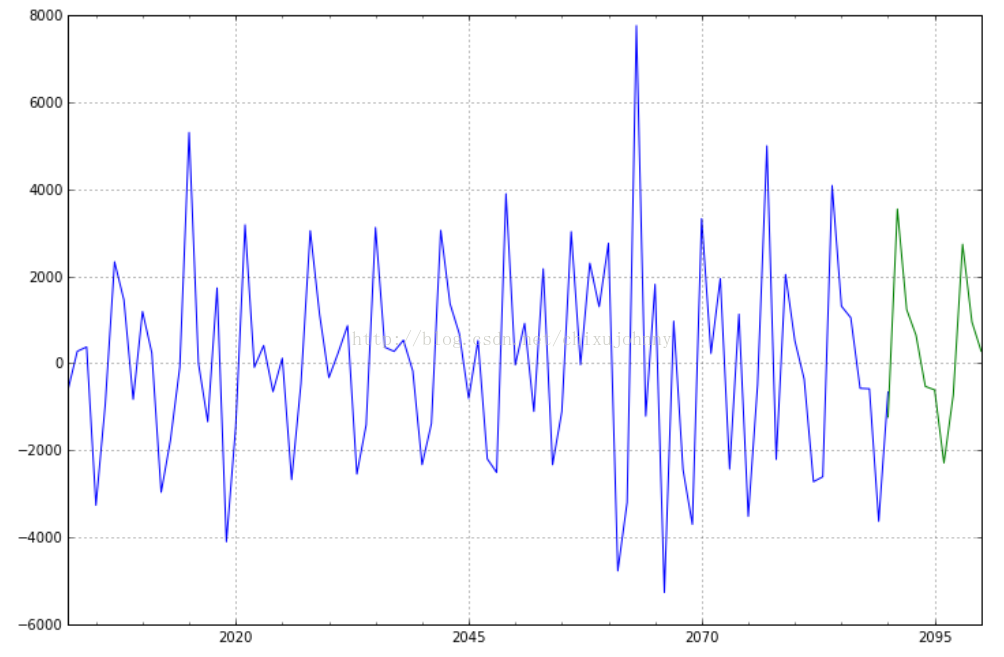
2）基于时间序列的预测：这个方法是在“阿里音乐流行趋势预测”竞赛中看到的，适用于一维时间序列的预测，主要应用在金融分析中比较多。使用的模型是ARIMA模型。优点是这套模型搞时间序列预测很专业，时间复杂度低，一次性预测未来好长时间的值。缺点是一维时间序列数据要先经过各种乱七八糟的变换，让数据足够规范化，才能进行时间序列预测。个人并不擅长这个，所以目前首选机器学习模型，搞好了有剩余时间了再搞一下ARIMA模型看看有没有惊喜，也许搞个双模型bagging融合也会是个亮点呢。做出的demo像下图中这样，绿色部分是预测值：

--------------------  3.13更新  --------------------

做完好几天了，一直没时间记录一下，我整理整理，后面有图和源码。      

这次试验还是选用上图那套具有不规律周期波动的demo数据，用机器学习的办法进行时间序列滚动预测，先说说结果吧，效果我个人感觉还算满意，做交叉验证的时候感觉确实能够预测未来的一些变化趋势。这个demo数据我个人感觉是一套很“复杂”的数据了，周期不太规律并且上下起伏非常的大，个别时间段还会出现波动比较爆炸的情况。如果在这套demo数据里预测的还可以，那在做服务特征分布预测的时候回轻松不少。

建模方法

这套滚动预测建模方法我是在天池大数据论坛里看到的，楼主说的也不详细，只是说了“滚动预测”，也没说说细节估计也是嫌麻烦没说。我只能开动脑筋想一下是咋“滚动”的。是这样：

以上面的数据为例，假设窗口大小为10，步进为1，首先选x1~x10这10个时间序列数据做X，再拿x11做目标值y建立第一个样本（为啥这么做，以及那俩参数咋选后面再说）上面一共有90个数据，如果拿10个数据作测试集的话，剩下80个数据做训练集。这80个具有严格先后顺序的数会被构建成69个样本，第一个样本上面说了，最后一个样本是x69~x79为X，x80为y，为啥是69个自己琢磨一下就行就不赘述了。

现在训练集就成了一个二维矩阵，每一行是一个样本，每一列是一个特征，这个特征是时间特征，可以理解为时间戳。我用机器学习里的回归模型进行建模的目的就是为了寻找数据波动和目标值之间的联系。充分学习数据的波动情况！

我把这69个样本扔进GBDT和RF里训练了一下，全部默认参数（够用了），那么机器现在已经比较充分的学习到这套时间序列数据的波动情况了。

下面说说滑窗和步进的选取：滑窗大小表示的是这个样本时间序列的“宽度”，太窄波动范围太小了，太宽又会导致样本比较少无法得到充分的训练，我觉得通过交叉验证选取最佳滑窗值比较好，步进是下一个滑窗离上一个滑窗滑动的距离，默认为1我觉得行，不同数据不同对待，依旧交叉验证选取最佳值。

由于我要预测10个数据，而不是一个，所以要把最新预测出来的那个数据扔进训练集再训练一遍才能预测第二个数。也就是说，预测的误差是逐渐扩大的，在实验中我也验证了这一点，时间序列数据的预测并不能预测的太远，再强的大牛也做不到。预测最近一段时间的还是可以的。

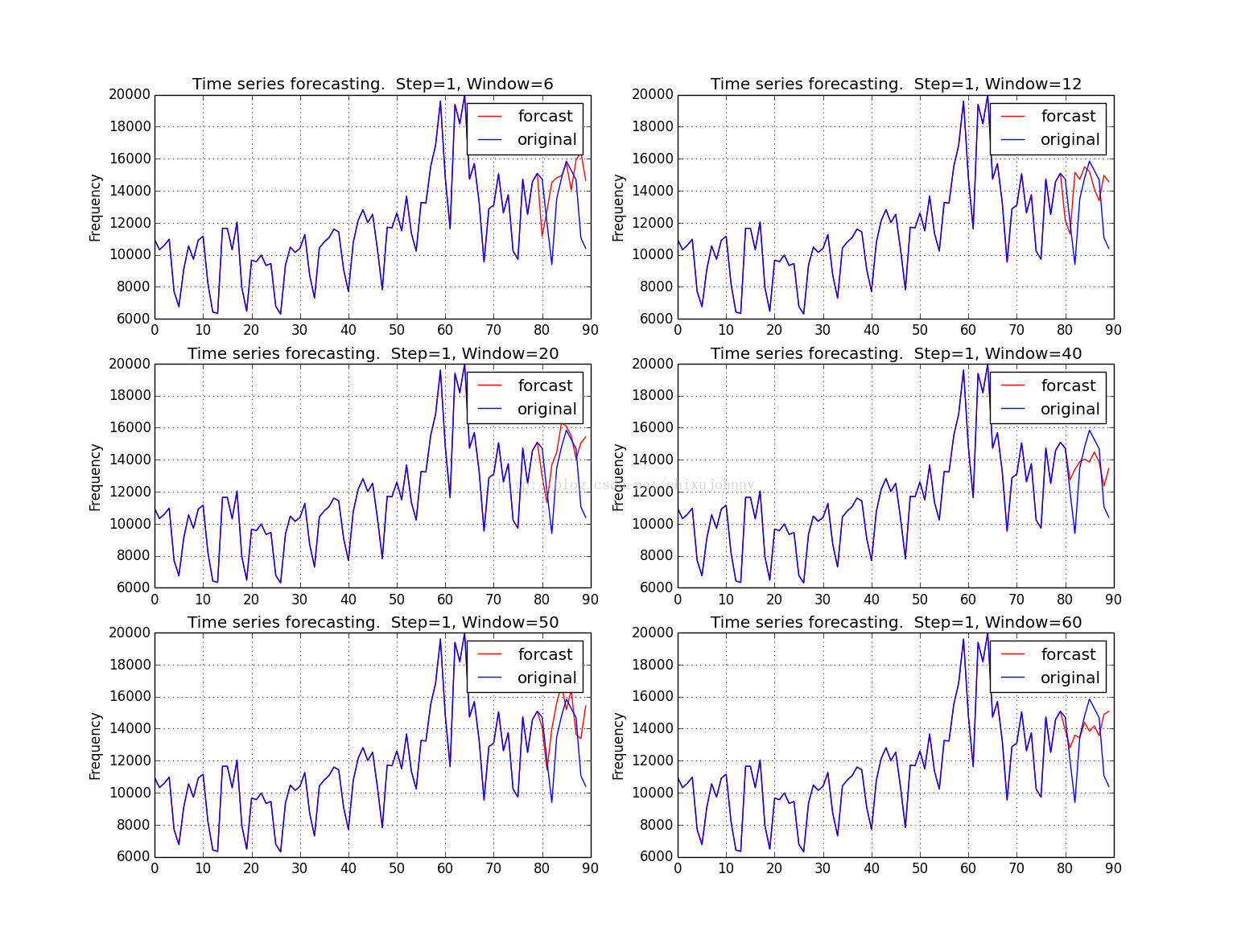
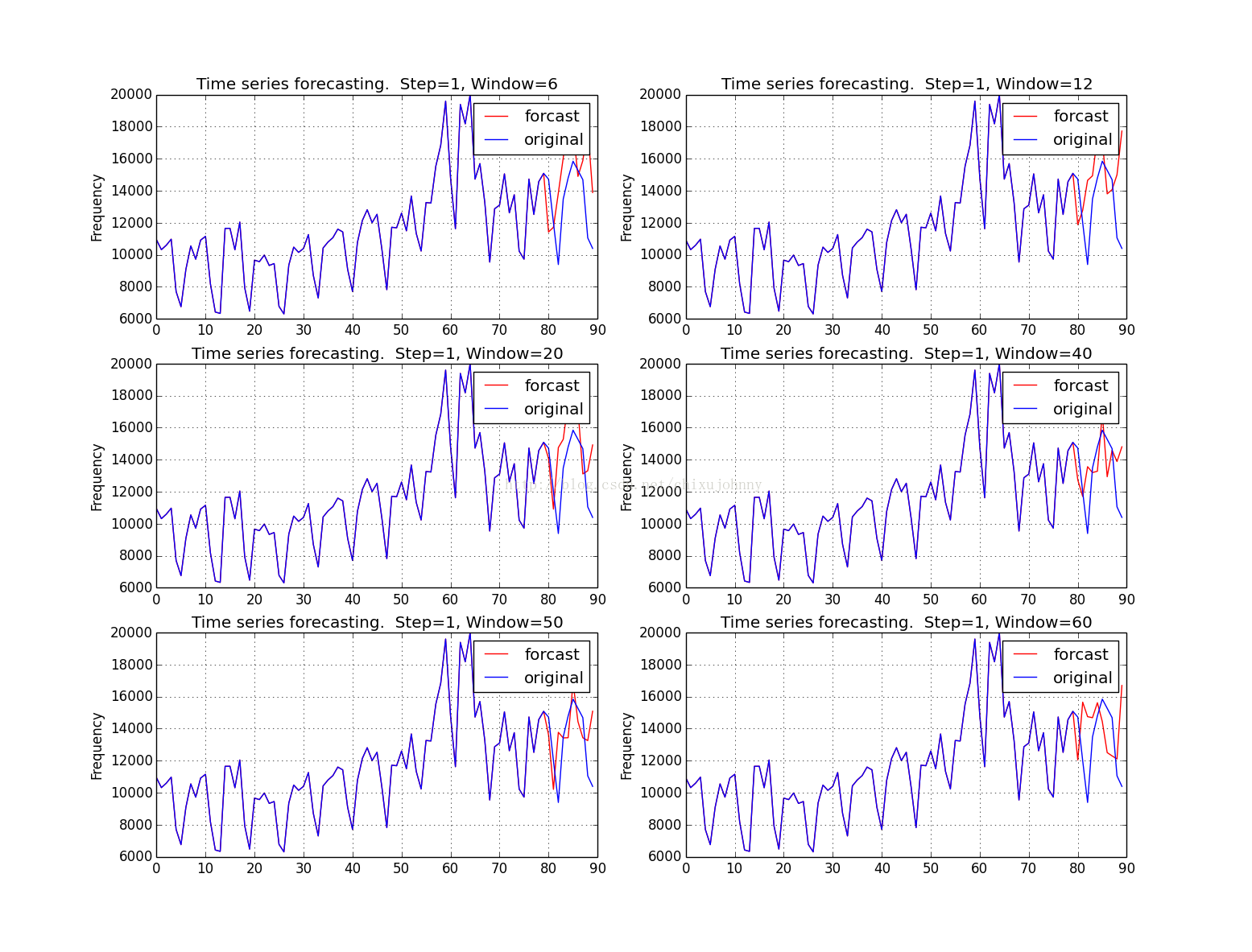
预测结果（随机森林RF）

预测结果（迭代回归树GBRT）

RF滑窗在20的时候预测的比较好，GBRT滑窗在50的时候预测的比较好，应该跟模型特质有关。

普遍问题：最后一个时间点的预测应该是向下波动的，预测成了向上波动，我觉得是个别情况，毕竟周期波动性数据预测难就难在这：你不知道什么时候往上走还是往下走，只要错开一点那趋势就完全反了还不如不预测。

源码：

# coding: utf-8

#
#  先选用 http://blog.csdn.net/u010414589/article/details/49622625 教程中的时间序列数据,用机器学习模型做个baseline
#


import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor
import copy

dta=[10930,10318,10595,10972,7706,6756,9092,10551,9722,10913,11151,8186,6422,
6337,11649,11652,10310,12043,7937,6476,9662,9570,9981,9331,9449,6773,6304,9355,
10477,10148,10395,11261,8713,7299,10424,10795,11069,11602,11427,9095,7707,10767,
12136,12812,12006,12528,10329,7818,11719,11683,12603,11495,13670,11337,10232,
13261,13230,15535,16837,19598,14823,11622,19391,18177,19994,14723,15694,13248,
9543,12872,13101,15053,12619,13749,10228,9725,14729,12518,14564,15085,14722,
11999,9390,13481,14795,15845,15271,14686,11054,10395]


# 先观察一下数据
'''
dta = pd.Series(dta) # 做成时间序列模式
dta.index = pd.Index(sm.tsa.datetools.dates_from_range('2001','2090'))
dta.plot(figsize=(12,8)) # 最佳尺寸(20,11.5)
plt.show()'''


# 使用 RF/GBRT 预测一下最后5个年份的数据
train = [10930,10318,10595,10972,7706,6756,9092,10551,9722,10913,11151,8186,6422,
6337,11649,11652,10310,12043,7937,6476,9662,9570,9981,9331,9449,6773,6304,9355,
10477,10148,10395,11261,8713,7299,10424,10795,11069,11602,11427,9095,7707,10767,
12136,12812,12006,12528,10329,7818,11719,11683,12603,11495,13670,11337,10232,
13261,13230,15535,16837,19598,14823,11622,19391,18177,19994,14723,15694,13248,
9543,12872,13101,15053,12619,13749,10228,9725,14729,12518,14564,15085]
test = [14722,
11999,9390,13481,14795,15845,15271,14686,11054,10395]

windows = [45,47,49,50,52,55]# 设置一个滑窗
plt.figure(figsize=(15, 11.5))

for w,window in enumerate(windows):

    train_new = copy.deepcopy(train)
    output = []

    for round in range(20):

        train_X = []
        train_y = []

        for i in range(len(train_new)-window-1):

            train_X.append(train_new[i:i+window])
            train_y.append([train_new[i+window+1]])

        train_X = np.array(train_X)
        train_y = np.array(train_y)
        model = GradientBoostingRegressor()  # GBRT模型
        # model = RandomForestRegressor()  # RF模型
        model.fit(train_X, train_y)
        test_X = train_new[-window:]
        predicted = model.predict(test_X)
        print predicted[0]
        output.append(predicted)
        train_new.append(predicted[0])
    if w <= 1:
        plt.subplot2grid((3,2), (0,0+w))
    elif w<= 3:
        plt.subplot2grid((3,2), (1,w-2))
    else:
        plt.subplot2grid((3,2), (2,w-4))
    plt.title('Time series forecasting.  Step=1, Window=' + str(window))
    # plt.xlabel('Date')
    plt.ylabel('Frequency')
    plt.plot(train + output, color='r', label='forcast') #  预测值
    plt.plot(train + test, label='original') # 原始值
    plt.legend()
    plt.grid(True)

plt.show()